Muchas de las propiedades físicas de las soluciones difieren significativamente de las de las sustancias puras discutidas en capítulos anteriores, y estas diferencias tienen consecuencias importantes. Por ejemplo, el rango de temperatura limitado del agua líquida (0 ° C – 100 ° C) limita severamente su uso. Las soluciones acuosas tienen un punto de congelación más bajo y un punto de ebullición más alto que el agua pura. Probablemente una de las aplicaciones más familiares de este fenómeno es la adición de etilenglicol (“anticongelante”) al agua en un radiador de automóvil. Este soluto reduce el punto de congelación del agua, evitando que el motor se raje en climas muy fríos debido a la expansión del agua pura al congelarse. El anticongelante también permite que el sistema de enfriamiento funcione a temperaturas superiores a 100 ° C sin generar suficiente presión para explotar.
Los cambios en el punto de congelación y el punto de ebullición de una solución dependen principalmente del número de partículas de soluto presentes en lugar del tipo de partículas. Dichas propiedades de las soluciones se denominan propiedades coligativas (del latín colligatus, que significa “unidos” como en una cantidad). Como veremos, la presión de vapor y la presión osmótica de las soluciones también son propiedades coligativas.
Presión de vapor de soluciones y ley de Raoult
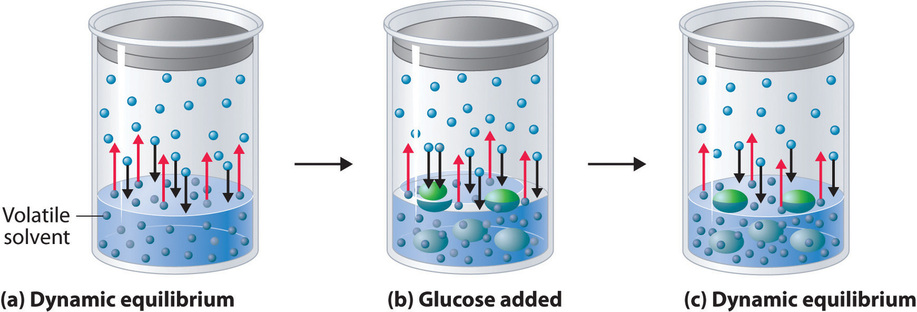
Agregar un soluto no volátil, uno cuya presión de vapor es demasiado baja para medir fácilmente, a un solvente volátil disminuye la presión de vapor del solvente. Podemos entender este fenómeno cualitativamente examinando la Figura ( PageIndex {1} ), que es un diagrama esquemático de la superficie de una solución de glucosa en agua. En una solución acuosa de glucosa, una porción del área de la superficie está ocupada por moléculas de glucosa no volátiles en lugar de por moléculas de agua volátiles. Como resultado, pueden ingresar menos moléculas de agua en la fase de vapor por unidad de tiempo, a pesar de que las moléculas de agua superficial tienen la misma distribución de energía cinética que tendrían en agua pura. Al mismo tiempo, la velocidad a la que las moléculas de agua en la fase de vapor chocan con la superficie y vuelven a entrar en la solución no se ve afectada. El efecto neto es cambiar el equilibrio dinámico entre el agua en las fases de vapor y líquido, disminuyendo la presión de vapor de la solución en comparación con la presión de vapor del disolvente puro.
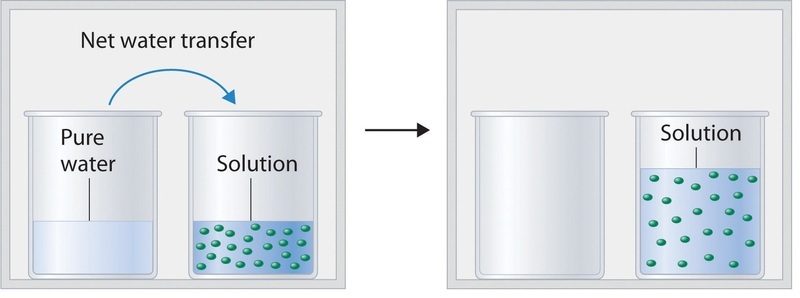
La figura ( PageIndex {2} ) muestra dos vasos de precipitados, uno que contiene agua pura y otro que contiene una solución acuosa de glucosa, en una cámara sellada. Podemos ver que el sistema tiene dos equilibrios competitivos: el vapor de agua se condensará en ambos vasos de precipitados a la misma velocidad, pero las moléculas de agua se evaporarán más lentamente de la solución de glucosa porque hay menos moléculas de agua en la superficie. Finalmente, toda el agua se evaporará del vaso que contiene el líquido con la presión de vapor más alta (agua pura) y se condensará en el vaso que contiene el líquido con la presión de vapor más baja (la solución de glucosa). Si el sistema consistiera solo en un vaso de precipitados de agua dentro de un recipiente sellado, el equilibrio entre el líquido y el vapor se lograría con bastante rapidez, y la cantidad de agua líquida en el vaso de precipitados permanecería constante.
Si las partículas de un soluto son esencialmente del mismo tamaño que las del solvente y tanto el soluto como el solvente tienen probabilidades aproximadamente iguales de estar en la superficie de la solución, entonces el efecto de un soluto sobre la presión de vapor del solvente es proporcional al número de sitios ocupados por partículas de soluto en la superficie de la solución. Duplicar la concentración de un soluto dado hace que el doble de sitios de superficie sean ocupados por moléculas de soluto, lo que resulta en el doble de la disminución de la presión de vapor. Por lo tanto, la relación entre la composición de la solución y la presión de vapor es
[P_A = chi_AP ^ 0_A label {13.5.1} ]
donde (P_A ) es la presión de vapor del componente A de la solución (en este caso, el solvente), ( chi_A ) es la fracción molar de (A ) en solución y (P ^ 0_A ) es la presión de vapor de puro (A ). La ecuación ( ref {13.5.1} ) se conoce como la ley de Raoult , en honor al químico francés que la desarrolló. Si la solución contiene solo un soluto no volátil (B), entonces ( chi_A + chi_B = 1 ), y podemos sustituir ( chi_A = 1 – chi_B ) para obtener
[ begin {align} P_A & = (1− chi_B) P ^ 0_A \ [4pt] & = P ^ 0_A− chi_BP ^ 0_A label {13.5.2} end {align} ]
Reordenando y definiendo (ΔP_A = P ^ 0_A − P_A ), obtenemos una relación entre la disminución de la presión de vapor y la fracción molar del soluto no volátil:
[ begin {align} P ^ 0_A − P_A & = ΔP_A \ [4pt] & = chi_BP ^ 0_A label {13.5.3} end {align} ]
Podemos resolver problemas de presión de vapor de dos maneras: usando la Ecuación ( ref {13.5.1} ) para calcular la presión de vapor real sobre una solución de un soluto no volátil, o usando la Ecuación ( ref {13.5.3} ) para calcular la disminución en la presión de vapor causada por una cantidad específica de un soluto no volátil.
Incluso cuando un soluto es volátil, lo que significa que tiene una presión de vapor medible, aún podemos usar la ley de Raoult. En este caso, calculamos la presión de vapor de cada componente por separado. La presión de vapor total de la solución ( (P_ {tot} )) es la suma de las presiones de vapor de los componentes:
[P_ {tot} = P_A + P_B = chi_AP ^ 0_A + chi_BP ^ 0_B label {13.5.4} ]
Porque ( chi_B = 1 – chi_A ) para un sistema de dos componentes,
[P_ {tot} = chi_AP ^ 0_A + (1− chi_A) P ^ 0_B label {13.5.5} ]
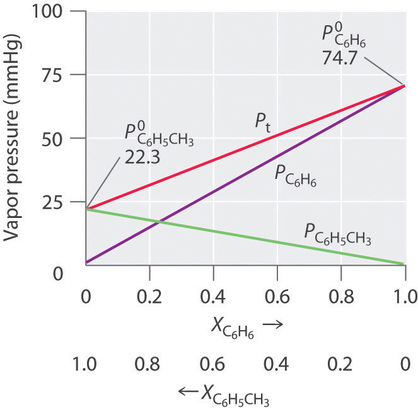
Por lo tanto, necesitamos especificar la fracción molar de solo uno de los componentes en un sistema de dos componentes. Considere, por ejemplo, la presión de vapor de soluciones de benceno y tolueno de diversas composiciones. A 20 ° C, las presiones de vapor de benceno puro y tolueno son 74.7 y 22.3 mmHg, respectivamente. La presión de vapor del benceno en una solución de benceno-tolueno es
[P_ {C_6H_6} = chi_ {C_6H_6} P ^ 0_ {C_6H_6} label {13.5.6} ]
y la presión de vapor de tolueno en la solución es
[P {C_6H_5CH_3} = chi_ {C_6H_5CH_3} P ^ 0_ {C_6H_5CH3} label {13.5.7} ]
Las ecuaciones ( ref {13.5.6} ) y ( ref {13.5.7} ) están en la forma de la ecuación para una línea recta: (y = mx + b ), donde (b = 0 ). Las gráficas de las presiones de vapor de ambos componentes versus las fracciones molares son, por lo tanto, líneas rectas que pasan a través del origen, como se muestra en la Figura ( PageIndex {3} ). Además, una gráfica de la presión de vapor total de la solución versus la fracción molar es una línea recta que representa la suma de las presiones de vapor de los componentes puros. Por lo tanto, la presión de vapor de la solución es siempre mayor que la presión de vapor de cualquiera de los componentes.
Una solución de dos componentes volátiles que se comporta como la solución de la Figura ( PageIndex {3} ), que se define como una solución que obedece la ley de Raoult. Como un gas ideal, una solución ideal es un sistema hipotético cuyas propiedades se pueden describir en términos de un modelo simple. Las mezclas de benceno y tolueno se aproximan a una solución ideal porque las fuerzas intermoleculares en los dos líquidos puros son casi idénticas tanto en clase como en magnitud. En consecuencia, el cambio en la entalpía en la formación de la solución es esencialmente cero ( (ΔH_ {soln} ≈ 0 )), que es una de las características definitorias de una solución ideal.
Sin embargo, la mayoría de las soluciones reales no obedecen la ley de Raoult con precisión, al igual que la mayoría de los gases reales no obedecen exactamente la ley del gas ideal. Las soluciones reales generalmente se desvían de la ley de Raoult porque las interacciones intermoleculares entre los dos componentes A y B difieren. Podemos distinguir entre dos tipos generales de comportamiento, dependiendo de si las interacciones intermoleculares entre las moléculas A y B son más fuertes o más débiles que las interacciones A – A y B – B en los componentes puros. Si las interacciones A – B son más fuertes que las interacciones A – A y B – B, cada componente de la solución exhibe una presión de vapor más baja de lo esperado para una solución ideal, al igual que la solución en su conjunto. Las interacciones favorables A – B estabilizan efectivamente la solución en comparación con el vapor. Este tipo de comportamiento se llama una desviación negativa de la ley de Raoult. Los sistemas estabilizados por enlaces de hidrógeno entre dos moléculas, como la acetona y el etanol, exhiben desviaciones negativas de la ley de Raoult. Por el contrario, si las interacciones A – B son más débiles que las interacciones A – A y B – B, sin embargo, el aumento de entropía es suficiente para permitir que se forme la solución, tanto A como B tienen una mayor tendencia a escapar de la solución a la fase de vapor. . El resultado es una presión de vapor más alta de lo esperado para una solución ideal, produciendo una desviación positiva de la ley de Raoult. En una solución de ( ce {CCl_4} ) y metanol, por ejemplo, las moléculas no polares ( ce {CCl_4} ) interrumpen la extensa red de enlaces de hidrógeno en metanol, y las moléculas de metanol más ligeras tienen fuerzas de dispersión más débiles en Londres que las moléculas más pesadas ( ce {CCl_4} ). En consecuencia, las soluciones de ( ce {CCl_4} ) y metanol exhiben desviaciones positivas de la ley de Raoult.
Elevación del punto de ebullición
Recuerde que el punto de ebullición normal de una sustancia es la temperatura a la cual la presión de vapor es igual a 1 atm. Si un soluto no volátil disminuye la presión de vapor de un solvente, también debe afectar el punto de ebullición. Debido a que la presión de vapor de la solución a una temperatura dada es menor que la presión de vapor del solvente puro, lograr una presión de vapor de 1 atm para la solución requiere una temperatura más alta que el punto de ebullición normal del solvente. Por lo tanto, el punto de ebullición de una solución es siempre mayor que el del disolvente puro. Podemos ver por qué esto debe ser cierto comparando el diagrama de fase para una solución acuosa con el diagrama de fase para agua pura (Figura ( PageIndex {4} )). La presión de vapor de la solución es menor que la del agua pura a todas las temperaturas. En consecuencia, la curva líquido-vapor para la solución cruza la línea horizontal correspondiente a P = 1 atm a una temperatura más alta que la curva para agua pura.
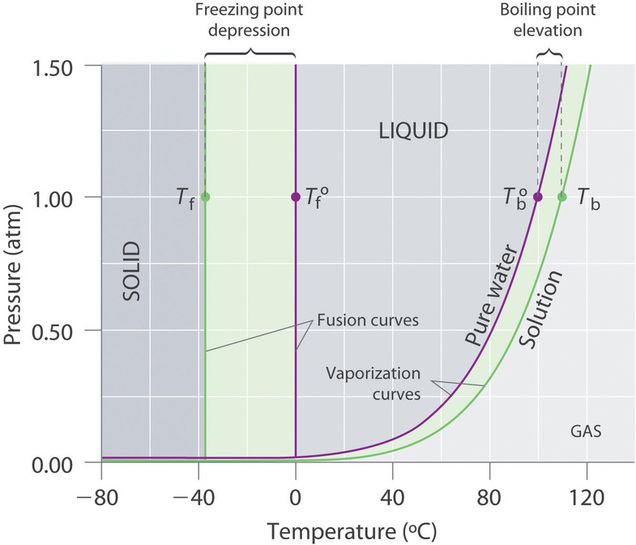
Figura ( PageIndex {4} ): Diagramas de fase de agua pura y una solución acuosa de un soluto no volátil. La curva de vaporización para la solución se encuentra debajo de la curva para agua pura a todas las temperaturas, lo que resulta en un aumento en el punto de ebullición y una disminución en el punto de congelación de la solución.
El punto de ebullición de una solución con un soluto no volátil es siempre mayor que el punto de ebullición del disolvente puro.
La magnitud del aumento en el punto de ebullición está relacionada con la magnitud de la disminución de la presión de vapor. Como acabamos de comentar, la disminución de la presión de vapor es proporcional a la concentración del soluto en la solución. Por lo tanto, la magnitud del aumento en el punto de ebullición también debe ser proporcional a la concentración del soluto (Figura ( PageIndex {5} )).
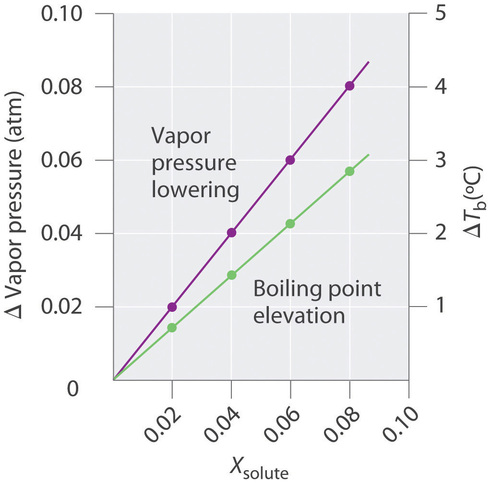
Podemos definir la elevación del punto de ebullición ( (ΔT_b )) como la diferencia entre los puntos de ebullición de la solución y el disolvente puro:
[ΔT_b = T_b − T ^ 0_b label {13.5.8} ]
donde (T_b ) es el punto de ebullición de la solución y (T ^ 0_b ) es el punto de ebullición del disolvente puro. Podemos expresar la relación entre (ΔT_b ) y la concentración de la siguiente manera
[ΔT_b = mK_b label {13.5.9} ]
donde m es la concentración del soluto expresado en molalidad, y (K_b ) es la constante de elevación del punto de ebullición molal del disolvente, que tiene unidades de ° C / m. La tabla ( PageIndex {1} ) enumera los valores característicos (K_b ) para varios solventes de uso común. Para soluciones relativamente diluidas, la magnitud de ambas propiedades es proporcional a la concentración de soluto.
| Disolvente | Punto de ebullición (° C) | K b (° C / m) | Punto de congelación (° C) | K f (° C / m) |
|---|---|---|---|---|
| ácido acético | 117,90 | 3,22 | 16,64 | 3,63 |
| benceno | 80.09 | 2,64 | 5,49 | 5.07 |
| d – (+) – alcanfor | 207,4 | 4,91 | 178,8 | 37,8 |
| disulfuro de carbono | 46,2 | 2,42 | −112,1 | 3,74 |
| tetracloruro de carbono | 76,8 | 5,26 | −22,62 | 31,4 |
| cloroformo | 61,17 | 3,80 | −63,41 | 4,60 |
| nitrobenceno | 210,8 | 5,24 | 5,70 | 6,87 |
| agua | 100,00 | 0,51 | 0,00 | 1,86 |
La concentración del soluto se expresa típicamente como molalidad en lugar de fracción molar o molaridad por dos razones. Primero, debido a que la densidad de una solución cambia con la temperatura, el valor de la molaridad también varía con la temperatura. Si el punto de ebullición depende de la concentración de soluto, entonces, por definición, el sistema no se mantiene a una temperatura constante. En segundo lugar, la molalidad y la fracción molar son proporcionales para soluciones relativamente diluidas, pero la molalidad tiene un valor numérico mayor (una fracción molar puede ser solo entre cero y uno). El uso de la molalidad nos permite eliminar los ceros no significativos.
Según la Tabla ( PageIndex {1} ), la constante de elevación del punto de ebullición molar para el agua es de 0,51 ° C / m. Así, una solución acuosa de 1,00 m de un soluto molecular no volátil como glucosa o sacarosa tendrá un aumento en el punto de ebullición de 0,51 ° C, para dar un punto de ebullición de 100,51 ° C a 1,00 atm. El aumento en el punto de ebullición de una solución acuosa ( ce {NaCl} ) de 1.00 m será aproximadamente dos veces mayor que el de la solución de glucosa o sacarosa porque 1 mol de ( ce {NaCl} ) produce 2 mol de iones disueltos. Por lo tanto, una solución de 1.00 m ( ce {NaCl} ) tendrá un punto de ebullición de aproximadamente 101.02 ° C.
Depresión del punto de congelación
El diagrama de fase en la Figura ( PageIndex {4} ) muestra que la disolución de un soluto no volátil en agua no solo aumenta el punto de ebullición del agua sino que también disminuye su punto de congelación. La curva sólido-líquido para la solución cruza la línea correspondiente a (P = 1 , atm ) a una temperatura más baja que la curva para agua pura.
Podemos entender este resultado imaginando que tenemos una muestra de agua a la temperatura normal del punto de congelación, donde hay un equilibrio dinámico entre sólido y líquido. Las moléculas de agua chocan continuamente con la superficie del hielo y entran en la fase sólida al mismo ritmo que las moléculas de agua salen de la superficie del hielo y entran en la fase líquida. Si disolvemos un soluto no volátil como la glucosa en el líquido, las moléculas de glucosa disueltas reducirán el número de colisiones por unidad de tiempo entre las moléculas de agua y la superficie del hielo porque algunas de las moléculas que colisionan con el hielo serán glucosa. Sin embargo, la glucosa tiene una estructura muy diferente que el agua, y no puede caber en la red de hielo. En consecuencia, la presencia de moléculas de glucosa en la solución solo puede disminuir la velocidad a la que las moléculas de agua en el líquido colisionan con la superficie del hielo y se solidifican. Mientras tanto, la velocidad a la que las moléculas de agua salen de la superficie del hielo y entran en la fase líquida no cambia. El efecto neto es hacer que el hielo se derrita. La única forma de restablecer un equilibrio dinámico entre el agua sólida y líquida es disminuir la temperatura del sistema, lo que disminuye la velocidad a la que las moléculas de agua salen de la superficie de los cristales de hielo hasta que es igual a la velocidad a la que chocan las moléculas de agua en la solución con el hielo
Por analogía con nuestro tratamiento de la elevación del punto de ebullición, la depresión del punto de congelación ( (ΔT_f )) se define como la diferencia entre el punto de congelación del disolvente puro y el punto de congelación de la solución:
[ΔT_f = T ^ 0_f − T_f label {13.5.10} ]
donde (T ^ 0_f ) es el punto de congelación del disolvente puro y (T_f ) es el punto de congelación de la solución.
El orden de los términos se invierte en comparación con la ecuación ( ref {13.5.8} ) para expresar la depresión del punto de congelación como un número positivo. La relación entre (ΔT_f ) y la concentración de soluto está dada por una ecuación análoga a la Ecuación ( ref {13.5.9} ):
[ΔT_f = mK_f label {13.5.11} ]
donde (m ) es la molalidad de la solución y (K_f ) es la constante de depresión del punto de congelación molal para el solvente (en unidades de ° C / m).
Al igual que (K_b ), cada solvente tiene un valor característico de (K_f ) (consulte la Tabla ( PageIndex {1} )). La depresión del punto de congelación depende del número total de partículas de soluto no volátiles disueltas, al igual que con la elevación del punto de ebullición. Así, una solución acuosa ( ce {NaCl} ) tiene una depresión del punto de congelación dos veces mayor que una solución de glucosa de la misma molalidad.
Las personas que viven en climas fríos utilizan la depresión del punto de congelación en su beneficio de muchas maneras. For example, salt is used to melt ice and snow on roads and sidewalks, ethylene glycol is added to engine coolant water to prevent an automobile engine from being destroyed, and methanol is added to windshield washer fluid to prevent the fluid from freezing.
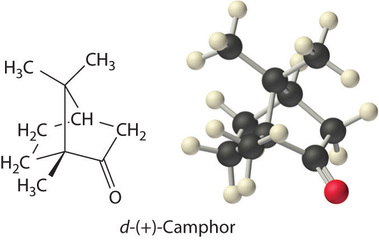
Colligative properties can also be used to determine the molar mass of an unknown compound. One method that can be carried out in the laboratory with minimal equipment is to measure the freezing point of a solution with a known mass of solute. This method is accurate for dilute solutions (≤1% by mass) because changes in the freezing point are usually large enough to measure accurately and precisely. By comparing (K_b) and (K_f) values in Table (PageIndex{1}), we see that changes in the boiling point are smaller than changes in the freezing point for a given solvent. Boiling point elevations are thus more difficult to measure precisely. For this reason, freezing point depression is more commonly used to determine molar mass than is boiling point elevation. Because of its very large value of (K_f) (37.8°C/m), d-(+)-camphor (Table (PageIndex{1})) is often used to determine the molar mass of organic compounds by this method.
Osmotic Pressure
Osmotic pressure is a colligative property of solutions that is observed using a semipermeable membrane, a barrier with pores small enough to allow solvent molecules to pass through but not solute molecules or ions. The net flow of solvent through a semipermeable membrane is called osmosis (from the Greek osmós, meaning “push”). The direction of net solvent flow is always from the side with the lower concentration of solute to the side with the higher concentration.
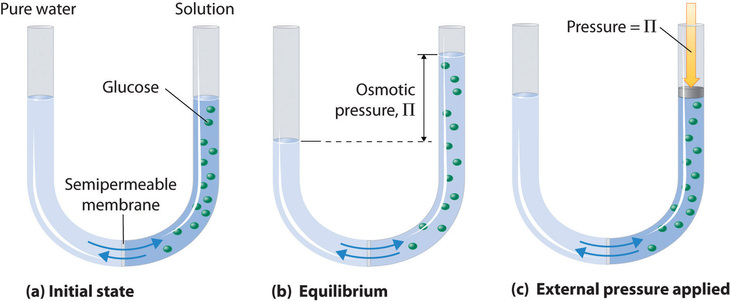
Osmosis can be demonstrated using a U-tube like the one shown in Figure (PageIndex{6}), which contains pure water in the left arm and a dilute aqueous solution of glucose in the right arm. A net flow of water through the membrane occurs until the levels in the arms eventually stop changing, which indicates that equilibrium has been reached. The osmotic pressure ((Pi)) of the glucose solution is the difference in the pressure between the two sides, in this case the heights of the two columns. Although the semipermeable membrane allows water molecules to flow through in either direction, the rate of flow is not the same in both directions because the concentration of water is not the same in the two arms. The net flow of water through the membrane can be prevented by applying a pressure to the right arm that is equal to the osmotic pressure of the glucose solution.
Just as with any other colligative property, the osmotic pressure of a solution depends on the concentration of dissolved solute particles. Osmotic pressure obeys a law that resembles the ideal gas equation:
[Pi=dfrac{nRT}{V}=MRT label{13.5.12}]
where (M) is the number of moles of solute per unit volume of solution (i.e., the molarity of the solution), (R) is the ideal gas constant, and (T) is the absolute temperature.
As shown in Example (PageIndex{7}), osmotic pressures tend to be quite high, even for rather dilute solutions.
Because of the large magnitude of osmotic pressures, osmosis is extraordinarily important in biochemistry, biology, and medicine. Virtually every barrier that separates an organism or cell from its environment acts like a semipermeable membrane, permitting the flow of water but not solutes. The same is true of the compartments inside an organism or cell. Some specialized barriers, such as those in your kidneys, are slightly more permeable and use a related process called dialysis, which permits both water and small molecules to pass through but not large molecules such as proteins.
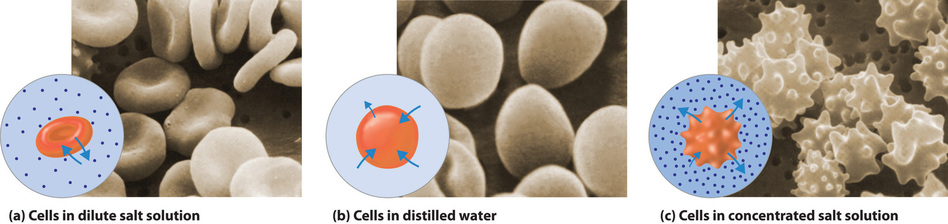
The same principle has long been used to preserve fruits and their essential vitamins over the long winter. High concentrations of sugar are used in jams and jellies not for sweetness alone but because they greatly increase the osmotic pressure. Thus any bacteria not killed in the cooking process are dehydrated, which keeps them from multiplying in an otherwise rich medium for bacterial growth. A similar process using salt prevents bacteria from growing in ham, bacon, salt pork, salt cod, and other preserved meats. The effect of osmotic pressure is dramatically illustrated in Figure (PageIndex{7}), which shows what happens when red blood cells are placed in a solution whose osmotic pressure is much lower or much higher than the internal pressure of the cells.
In addition to capillary action, trees use osmotic pressure to transport water and other nutrients from the roots to the upper branches. Evaporation of water from the leaves results in a local increase in the salt concentration, which generates an osmotic pressure that pulls water up the trunk of the tree to the leaves.
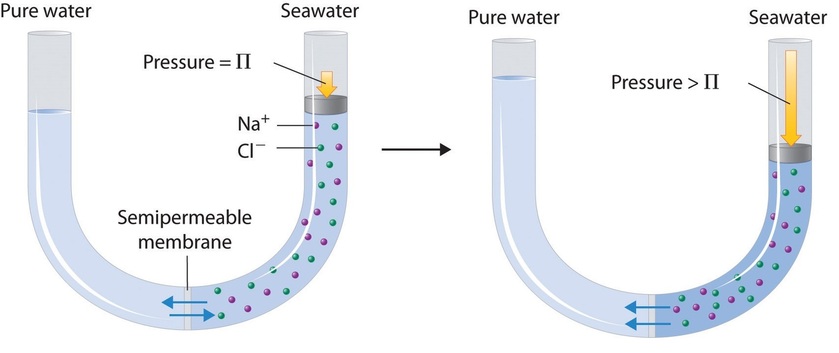
Finally, a process called reverse osmosis can be used to produce pure water from seawater. As shown schematically in Figure (PageIndex{8}), applying high pressure to seawater forces water molecules to flow through a semipermeable membrane that separates pure water from the solution, leaving the dissolved salt behind. Large-scale desalinization plants that can produce hundreds of thousands of gallons of freshwater per day are common in the desert lands of the Middle East, where they supply a large proportion of the freshwater needed by the population. Similar facilities are now being used to supply freshwater in southern California. Small, hand-operated reverse osmosis units can produce approximately 5 L of freshwater per hour, enough to keep 25 people alive, and are now standard equipment on US Navy lifeboats.
Colligative Properties of Electrolyte Solutions
Thus far we have assumed that we could simply multiply the molar concentration of a solute by the number of ions per formula unit to obtain the actual concentration of dissolved particles in an electrolyte solution. We have used this simple model to predict such properties as freezing points, melting points, vapor pressure, and osmotic pressure. If this model were perfectly correct, we would expect the freezing point depression of a 0.10 m solution of sodium chloride, with 2 mol of ions per mole of (ce{NaCl}) in solution, to be exactly twice that of a 0.10 m solution of glucose, with only 1 mol of molecules per mole of glucose in solution. In reality, this is not always the case. Instead, the observed change in freezing points for 0.10 m aqueous solutions of (ce{NaCl}) and (ce{KCl}) are significantly less than expected (−0.348°C and −0.344°C, respectively, rather than −0.372°C), which suggests that fewer particles than we expected are present in solution.
The relationship between the actual number of moles of solute added to form a solution and the apparent number as determined by colligative properties is called the van’t Hoff factor ((i)) and is defined as follows:
[i=dfrac{text{apparent number of particles in solution}}{text{ number of moles of solute dissolved}} label{13.5.13}]
Named for Jacobus Hendricus van’t Hoff (1852–1911), a Dutch chemistry professor at the University of Amsterdam who won the first Nobel Prize in Chemistry (1901) for his work on thermodynamics and solutions.
As the solute concentration increases, the van’t Hoff factor decreases.
The van’t Hoff factor is therefore a measure of a deviation from ideal behavior . The lower the van’t Hoff factor, the greater the deviation. As the data in Table (PageIndex{2}) show, the van’t Hoff factors for ionic compounds are somewhat lower than expected; that is, their solutions apparently contain fewer particles than predicted by the number of ions per formula unit. As the concentration of the solute increases, the van’t Hoff factor decreases because ionic compounds generally do not totally dissociate in aqueous solution.
| Compound | i (measured) | i (ideal) |
|---|---|---|
| glucose | 1.0 | 1.0 |
| sucrose | 1.0 | 1.0 |
| (NaCl) | 1.9 | 2.0 |
| (HCl) | 1.9 | 2.0 |
| (MgCl_2) | 2.7 | 3.0 |
| (FeCl_3) | 3.4 | 4.0 |
| (Ca(NO_3)_2) | 2.5 | 3.0 |
| (AlCl_3) | 3.2 | 4.0 |
| (MgSO_4) | 1.4 | 2.0 |
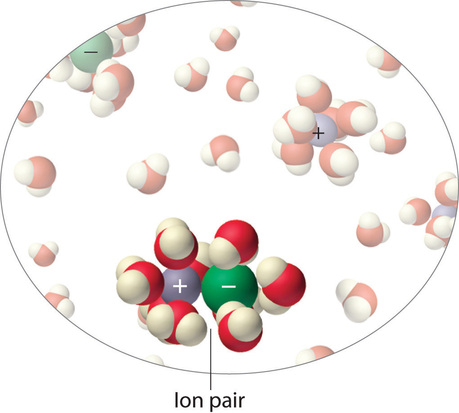
Instead, some of the ions exist as ion pairs, a cation and an anion that for a brief time are associated with each other without an intervening shell of water molecules (Figure (PageIndex{9})). Each of these temporary units behaves like a single dissolved particle until it dissociates. Highly charged ions such as (Mg^{2+}), (Al^{3+}), (SO_4^{2−}), and (PO_4^{3−}) have a greater tendency to form ion pairs because of their strong electrostatic interactions. The actual number of solvated ions present in a solution can be determined by measuring a colligative property at several solute concentrations.
Summary
The colligative properties of a solution depend on only the total number of dissolved particles in solution, not on their chemical identity. Colligative properties include vapor pressure, boiling point, freezing point, and osmotic pressure. The addition of a nonvolatile solute (one without a measurable vapor pressure) decreases the vapor pressure of the solvent. The vapor pressure of the solution is proportional to the mole fraction of solvent in the solution, a relationship known as Raoult’s law . Solutions that obey Raoult’s law are called ideal solutions. Most real solutions exhibit positive or negative deviations from Raoult’s law. The boiling point elevation ((ΔT_b)) and freezing point depression ((ΔT_f)) of a solution are defined as the differences between the boiling and freezing points, respectively, of the solution and the pure solvent. Both are proportional to the molality of the solute. When a solution and a pure solvent are separated by a semipermeable membrane, a barrier that allows solvent molecules but not solute molecules to pass through, the flow of solvent in opposing directions is unequal and produces an osmotic pressure, which is the difference in pressure between the two sides of the membrane. Osmosis is the net flow of solvent through such a membrane due to different solute concentrations. Dialysis uses a semipermeable membrane with pores that allow only small solute molecules and solvent molecules to pass through. In more concentrated solutions, or in solutions of salts with highly charged ions, the cations and anions can associate to form ion pairs, which decreases their effect on the colligative properties of the solution. The extent of ion pair formation is given by the van’t Hoff factor (i), the ratio of the apparent number of particles in solution to the number predicted by the stoichiometry of the salt.
- Henry’s law: [C = kP
onumber ] - Raoult’s law : [P_A=chi_AP^0_A
onumber ] - vapor pressure lowering : [P^0_A−P_A=ΔP_A=chi_BP^0_A
onumber ] - vapor pressure of a system containing two volatile components : [P_{tot}=chi_AP^0_A+(1−chi_A)P^0_B
onumber ] - boiling point elevation : [ΔT_b = mK_b
onumber ] - freezing point depression: [ΔT_f = mK_f
onumber ] - osmotic pressure : [Pi=nRTV=MRT
onumber ] - van’t Hoff factor : [i=dfrac{text{apparent number of particles in solution}}{text{ number of moles of solute dissolved}}
onumber ]