Las velocidades de reacción generalmente se expresan como la concentración de reactivo consumido o la concentración de producto formado por unidad de tiempo. Por lo tanto, las unidades son moles por litro por unidad de tiempo, escritas como M / s, M / min o M / h. Para medir las velocidades de reacción, los químicos inician la reacción, miden la concentración del reactivo o producto en diferentes momentos a medida que avanza la reacción, quizás grafican la concentración en función del tiempo en un gráfico y luego calculan el cambio en la concentración por unidad de tiempo .
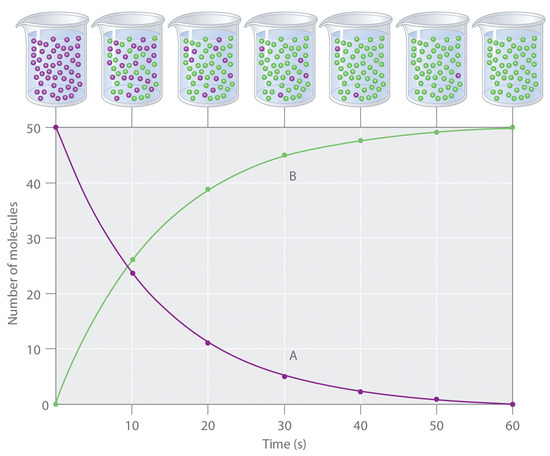
El progreso de una reacción simple (A → B) se muestra en Figura ( PageIndex {1} ); los vasos de precipitados son instantáneas de la composición de la solución a intervalos de 10 s. El número de moléculas de reactivo (A) y producto (B) se representa en función del tiempo en el gráfico. Cada punto en el gráfico corresponde a un vaso de precipitados en Figura ( PageIndex {1} ) . La velocidad de reacción es el cambio en la concentración del reactivo o del producto durante un período de tiempo. La concentración de A disminuye con el tiempo, mientras que la concentración de B aumenta con el tiempo.
[ textrm {tasa} = dfrac { Delta [ textrm B]} { Delta t} = – dfrac { Delta [ textrm A]} { Delta t} label {Eq1} ]
Los corchetes indican concentraciones molares, y la delta griega capital (Δ) significa “cambio en”. Debido a que los químicos siguen la convención de expresar todas las velocidades de reacción como números positivos, sin embargo, se inserta un signo negativo frente a Δ [A] / Δt para convertir esa expresión en un número positivo. La velocidad de reacción calculada para la reacción A → B usando la ecuación ( ref {Eq1} ) es diferente para cada intervalo (esto no es cierto para cada reacción, como se muestra a continuación). Se produce un cambio mayor en [A] y [B] durante el primer intervalo de 10 s, por ejemplo, que durante el último, lo que significa que la velocidad de reacción es mayor al principio.
Las velocidades de reacción generalmente disminuyen con el tiempo a medida que disminuyen las concentraciones de reactivo.
Determinación de la velocidad de reacción de hidrólisis de la aspirina
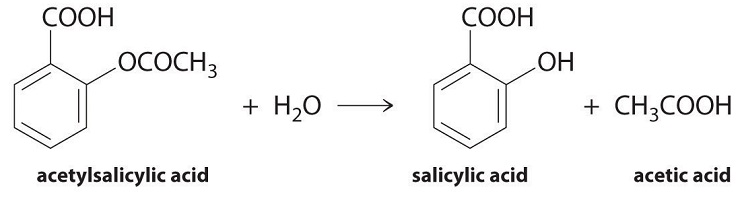
Podemos usar la Ecuación ( ref {Eq1} ) para determinar la velocidad de reacción de la hidrólisis de la aspirina, probablemente el fármaco más comúnmente usado en el mundo (se producen más de 25,000,000 kg anualmente en todo el mundo). La aspirina (ácido acetilsalicílico) reacciona con agua (como el agua en los fluidos corporales) para dar ácido salicílico y ácido acético, como se muestra en la Figura ( PageIndex {2} ).
Debido a que el ácido salicílico es la sustancia real que alivia el dolor y reduce la fiebre y la inflamación, una gran cantidad de investigación se ha centrado en comprender esta reacción y los factores que afectan su velocidad. Los datos para la hidrólisis de una muestra de aspirina se encuentran en la Tabla ( PageIndex {1} ) y se muestran en el gráfico en Figura ( PageIndex {3} ) .
| Tiempo (h) | [Aspirina] (M) | [Ácido salicílico] (M) |
|---|---|---|
| * La reacción a pH 7,0 es muy lenta. Es mucho más rápido en condiciones ácidas, como las que se encuentran en el estómago. | ||
| 0 | 5,55 × 10 −3 | 0 |
| 2,0 | 5,51 × 10 −3 | 0,040 × 10 −3 |
| 5.0 | 5,45 × 10 −3 | 0,10 × 10 −3 |
| 10 | 5,35 × 10 −3 | 0,20 × 10 −3 |
| 20 | 5,15 × 10 −3 | 0,40 × 10 −3 |
| 30 | 4,96 × 10 −3 | 0,59 × 10 −3 |
| 40 | 4,78 × 10 −3 | 0,77 × 10 −3 |
| 50 | 4,61 × 10 −3 | 0,94 × 10 −3 |
| 100 | 3,83 × 10 −3 | 1.72 × 10 −3 |
| 200 | 2,64 × 10 −3 | 2.91 × 10 −3 |
| 300 | 1,82 × 10 −3 | 3.73 × 10 −3 |
Los datos de la Tabla ( PageIndex {1} ) se obtuvieron eliminando muestras de la mezcla de reacción en los momentos indicados y analizándolas para determinar las concentraciones del reactivo (aspirina) y uno de los productos (ácido salicílico) .
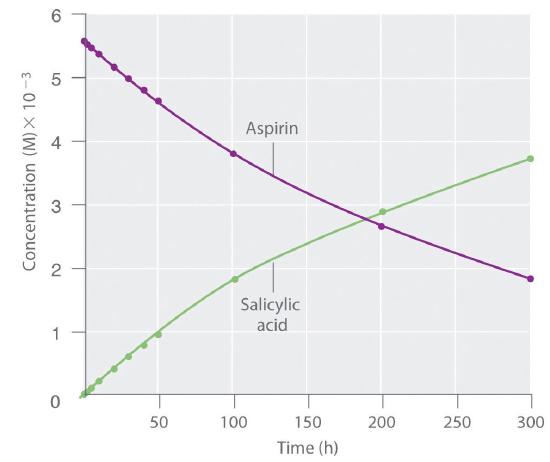
La velocidad de reacción promedio para un intervalo de tiempo dado se puede calcular a partir de las concentraciones del reactivo o de uno de los productos al comienzo del intervalo (tiempo = t 0 ) y al final del intervalo (t 1 ). Usando ácido salicílico, la velocidad de reacción para el intervalo entre t = 0 hyt = 2.0 h (recuerde que el cambio siempre se calcula como final menos inicial) se calcula de la siguiente manera:
[ begin {align} textrm {rate} _ {(t = 0-2.0 textrm {h})} & = frac {[ textrm {salicyclic acid}] _ 2 – [ textrm {salicyclic ácido}] _ 0} { textrm {2.0 h} – textrm {0 h}}
\ & = frac {0.040 times10 ^ {- 3} textrm {M} -0 textrm {M} } { textrm {2.0 h}} = 2.0 times10 ^ {- 5} textrm {M / h}
end {align} ]
La velocidad de reacción también se puede calcular a partir de las concentraciones de aspirina al principio y al final del mismo intervalo, recordando insertar un signo negativo, porque su concentración disminuye:
[ begin {align} textrm {rate} _ {(t = 0-2.0 textrm {h})} & = – dfrac {[ textrm {aspirin}] _ 2 – [ textrm {aspirin }] _ 0} { mathrm {2.0 , h-0 , h}}
\ & = – dfrac {(5.51 times10 ^ {- 3} textrm {M}) – (5.55 times10 ^ {- 3} textrm {M})} { textrm {2.0 h}}
\ & = 2 times10 ^ {- 5} textrm {M / h} end {align} ] [ 19459010]
Si la velocidad de reacción se calcula durante el último intervalo dado en la Tabla ( PageIndex {1} ) (el intervalo entre 200 hy 300 h después del inicio de la reacción), la velocidad de reacción es significativamente más lenta que fue durante el primer intervalo (t = 0–2.0 h):
[ begin {align} textrm {rate} _ {(t = 200-300 textrm {h})} & = dfrac {[ textrm {ácido salicíclico}] _ {300} – [ textrm {ácido salicílico}] _ {200}} { mathrm {300 , h-200 , h}}
\ & = – dfrac {(3.73 times10 ^ {- 3} textrm {M }) – (2.91 times10 ^ {- 3} textrm {M})} { textrm {100 h}}
\ & = 8.2 times10 ^ {- 6} textrm {M / h} end {align} ]
Cálculo de la velocidad de reacción de fermentación de la sacarosa
En el ejemplo anterior, los coeficientes estequiométricos en la ecuación química equilibrada son los mismos para todos los reactivos y productos; es decir, todos los reactivos y productos tienen el coeficiente 1. Considere una reacción en la que los coeficientes no son todos iguales, la fermentación de sacarosa a etanol y dióxido de carbono:
[ underset { textrm {sacarosa}} { mathrm {C_ {12} H_ {22} O_ {11} (aq)}} + mathrm {H_2O (l)} rightarrow mathrm {4C_2H_5OH (aq)} + 4 mathrm {CO_2 (g)} label {Eq2} ]
Los coeficientes indican que la reacción produce cuatro moléculas de etanol y cuatro moléculas de dióxido de carbono por cada molécula de sacarosa consumida. Como antes, la velocidad de reacción se puede encontrar a partir del cambio en la concentración de cualquier reactivo o producto. En este caso particular, sin embargo, un químico probablemente usaría la concentración de sacarosa o etanol porque los gases generalmente se miden como volúmenes y, como se explica en Capítulo 10 , el volumen de CO 2 [19459050 ] el gas formado depende del volumen total de la solución en estudio y la solubilidad del gas en la solución, no solo la concentración de sacarosa. Los coeficientes en la ecuación química equilibrada nos dicen que la velocidad de reacción a la que se forma el etanol es siempre cuatro veces más rápida que la velocidad de reacción a la que se consume la sacarosa:
[ dfrac { Delta [ mathrm {C_2H_5OH}]} { Delta t} = – dfrac {4 Delta [ textrm {sacarosa}]} { Delta t} label {Eq3} ]
La concentración del reactivo, en este caso sacarosa, disminuye con el tiempo, por lo que el valor de Δ [sacarosa] es negativo. En consecuencia, se inserta un signo menos delante de Δ [sacarosa] en Ecuación ( ref {Eq3} ) de modo que la tasa de cambio de la concentración de sacarosa se expresa como un valor positivo. Por el contrario, la concentración de etanol aumenta con el tiempo, por lo que su tasa de cambio se expresa automáticamente como un valor positivo.
A menudo, la velocidad de reacción se expresa en términos del reactivo o producto con el coeficiente más pequeño en la ecuación química equilibrada. El coeficiente más pequeño en la reacción de fermentación de sacarosa ( Ecuación ( ref {Eq2} ) ) corresponde a sacarosa, por lo que la velocidad de reacción generalmente se define de la siguiente manera:
[ textrm {rate} = – dfrac { Delta [ textrm {sucrose}]} { Delta t} = dfrac {1} {4} left ( dfrac { Delta [ mathrm {C_2H_5OH}]} { Delta t} right) label {Eq4} ]
Tasas de reacción instantáneas
La velocidad instantánea de una reacción es la velocidad de reacción en cualquier momento dado. A medida que el período de tiempo utilizado para calcular la velocidad promedio de una reacción se vuelve cada vez más corto, la velocidad promedio se aproxima a la velocidad instantánea. Comparando esto con el cálculo, la velocidad instantánea de una reacción en un momento dado corresponde a la pendiente de una línea tangente a la curva de concentración versus tiempo en ese punto, es decir, la derivada de la concentración con respecto al tiempo.
La distinción entre las tasas instantáneas y promedio de una reacción es similar a la distinción entre la velocidad real de un automóvil en un momento dado en un viaje y la velocidad promedio del automóvil para todo el viaje. Aunque el automóvil puede viajar durante un período prolongado a 65 mph en una carretera interestatal durante un viaje largo, puede haber momentos en los que viaja solo a 25 mph en zonas de construcción o 0 mph si se detiene por comidas o gasolina. La velocidad promedio en el viaje puede ser de solo 50 mph, mientras que la velocidad instantánea en la interestatal en un momento dado puede ser de 65 mph. Si el automóvil puede detenerse a tiempo para evitar un accidente depende de su velocidad instantánea, no de su velocidad promedio. Sin embargo, existen diferencias importantes entre la velocidad de un automóvil durante un viaje y la velocidad de una reacción química. La velocidad de un automóvil puede variar de manera impredecible a lo largo de un viaje, y la parte inicial de un viaje suele ser una de las más lentas. En una reacción química, el intervalo inicial generalmente tiene la velocidad más rápida (aunque este no es siempre el caso), y la velocidad de reacción generalmente cambia suavemente con el tiempo.
La cinética química generalmente se enfoca en una velocidad instantánea particular, que es la velocidad de reacción inicial, t = 0. Las velocidades iniciales se determinan midiendo la velocidad de reacción en varios momentos y luego extrapolando un gráfico de velocidad versus tiempo a t = 0.
Resumen
En este módulo, se demuestra la determinación cuantitativa de una velocidad de reacción. Las velocidades de reacción se pueden determinar en intervalos de tiempo particulares o en un punto dado en el tiempo. Una ley de velocidad describe la relación entre las velocidades de reactivo y las concentraciones de reactivo. Las tasas de reacción se informan como la tasa promedio durante un período de tiempo o como la tasa instantánea en un solo momento. Las velocidades de reacción se pueden determinar en intervalos de tiempo particulares o en un punto dado en el tiempo.
- Definición general de velocidad para A → B: [ textrm {velocidad} = frac { Delta [ textrm B]} { Delta t} = – frac { Delta [ textrm A]} { Delta t}
onumber ]