Se puede usar la ley de velocidad diferencial o la ley de velocidad integrada para determinar el orden de reacción a partir de datos experimentales. A menudo, los exponentes en la ley de velocidad son los enteros positivos: 1 y 2 o incluso 0. Por lo tanto, las reacciones son zeroth , primer o segundo orden en cada reactivo. Los patrones comunes utilizados para identificar el orden de reacción se describen en esta sección, donde nos centramos en los tipos característicos de las leyes de velocidad diferencial e integrada y cómo determinar el orden de reacción a partir de datos experimentales. El objetivo de aprendizaje de este módulo es saber cómo determinar el orden de reacción a partir de datos experimentales.
Reacciones de orden cero
Una reacción de orden cero es aquella cuya velocidad es independiente de la concentración; su ley de tasa diferencial es
[ text {rate} = k. ]
Nos referimos a estas reacciones como orden cero porque también podríamos escribir su velocidad en una forma tal que el exponente del reactivo en la ley de velocidad sea 0:
[ textrm {tasa} = – dfrac { Delta [ textrm A]} { Delta t} = k [ textrm {reactivo}] ^ 0 = k (1) = k etiqueta {14.4 .1} ]
Debido a que la velocidad es independiente de la concentración de reactivo, una gráfica de la concentración de cualquier reactivo en función del tiempo es una línea recta con una pendiente de (- k ). El valor de (k ) es negativo porque la concentración del reactivo disminuye con el tiempo. Por el contrario, una gráfica de la concentración de cualquier producto en función del tiempo es una línea recta con una pendiente de (k ), un valor positivo.
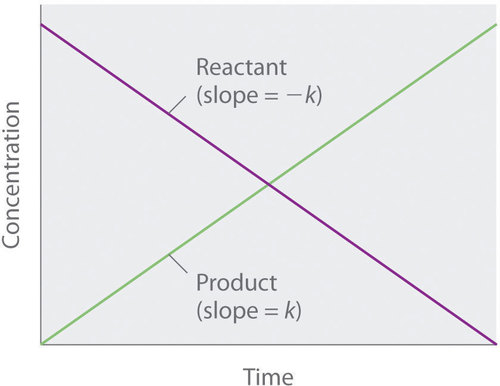
La gráfica de una reacción de orden cero. El cambio en la concentración de reactivo y producto con el tiempo produce una línea recta.
La ley de velocidad integrada para una reacción de orden cero también produce una línea recta y tiene la forma general
[[A] = [A] _0 – kt label {14.4.2} ]
donde ([A] _0 ) es la concentración inicial de reactivo (A ). La ecuación ( ref {14.4.2} ) tiene la forma de la ecuación algebraica para una línea recta,
[y = mx + b, ]
con (y = [A] ), (mx = −kt ) y (b = [A] _0 ).)
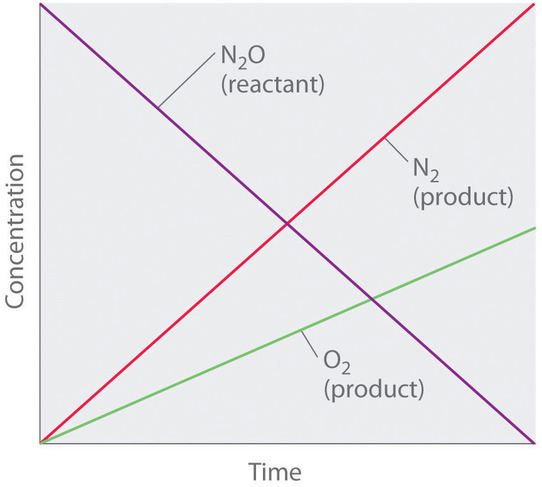
Aunque puede parecer contradictorio que la velocidad de reacción sea independiente de la (s) concentración (es) de reactivo, tales reacciones son bastante comunes. Ocurren con mayor frecuencia cuando la velocidad de reacción está determinada por el área de superficie disponible. Un ejemplo es la descomposición de N 2 O en una superficie de platino (Pt) para producir N 2 y O 2 , que ocurre a temperaturas que oscilan entre 200 ° C a 400 ° C:
[ mathrm {2N_2O (g)} xrightarrow { textrm {Pt}} mathrm {2N_2 (g)} + mathrm {O_2 (g)} label {14.4.3} ] [19459012 ]
Sin una superficie de platino, la reacción requiere temperaturas superiores a 700 ° C, pero entre 200 ° C y 400 ° C, el único factor que determina qué tan rápido se descompone N 2 O es la cantidad de Pt superficie disponible (no la cantidad de Pt). Mientras haya suficiente N 2 O para reaccionar con toda la superficie de Pt, duplicar o cuadruplicar la concentración de N 2 O no tendrá efecto en la velocidad de reacción. A concentraciones muy bajas de N 2 O, donde no hay suficientes moléculas presentes para ocupar toda la superficie de Pt disponible, la velocidad de reacción depende de la concentración de N 2 O. La velocidad de reacción es la siguiente:
[ textrm {rate} = – dfrac {1} {2} left ( dfrac { Delta [ mathrm {N_2O}]} { Delta t} right) = dfrac {1} {2} left ( dfrac { Delta [ mathrm {N_2}]} { Delta t} right) = dfrac { Delta [ mathrm {O_2}]} { Delta t} = k [ matemática {N_2O}] ^ 0 = k label {14.4.4} ]
Por lo tanto, la velocidad a la que se consume N 2 O y las velocidades a las que se producen N 2 y O 2 son independientes de la concentración. Como se muestra en Figura ( PageIndex {1} ) , el cambio en las concentraciones de todas las especies con el tiempo es lineal. Lo más importante, el exponente (0) correspondiente a la concentración de N 2 O en la ley de velocidad derivada experimentalmente no es el mismo que el coeficiente estequiométrico del reactivo en la ecuación química equilibrada (2). Para esta reacción, como para todas las demás, la ley de velocidad debe determinarse experimentalmente.
Una reacción de orden cero que tiene lugar en el hígado humano es la oxidación de etanol (de bebidas alcohólicas) a acetaldehído, catalizada por la enzima alcohol deshidrogenasa. A altas concentraciones de etanol, esta reacción también es una reacción de orden cero. La ecuación de reacción general es

donde NAD + (dinucleótido de nicotinamida y adenina) y NADH (dinucleótido de nicotinamida y adenina reducida) son las formas oxidadas y reducidas, respectivamente, de una especie utilizada por todos los organismos para transportar electrones. Cuando se consume una bebida alcohólica, el etanol se absorbe rápidamente en la sangre. Luego, su concentración disminuye a una velocidad constante hasta llegar a cero (parte (a) en Figura ( PageIndex {3} )). Una persona promedio de 70 kg generalmente toma alrededor de 2.5 h para oxidar los 15 ml de etanol contenidos en una lata de cerveza de 12 onzas, un vaso de vino de 5 onzas o un trago de licores destilados (como whisky o brandy). Sin embargo, la tasa real varía mucho de persona a persona, dependiendo del tamaño del cuerpo y la cantidad de alcohol deshidrogenasa en el hígado. La velocidad de reacción no aumenta si se consume una mayor cantidad de alcohol durante el mismo período de tiempo porque la velocidad de reacción está determinada solo por la cantidad de enzima presente en el hígado. Contrariamente a la creencia popular, la cafeína en el café es ineficaz para catalizar la oxidación del etanol. Cuando el etanol ha sido completamente oxidado y su concentración cae esencialmente a cero, la tasa de oxidación también cae rápidamente (parte (b) en Figura ( PageIndex {3} )).

Estos ejemplos ilustran dos puntos importantes:
- En una reacción de orden cero, la velocidad de reacción no depende de la concentración de reactivo.
- Un cambio lineal en la concentración con el tiempo es una clara indicación de una reacción de orden cero.
Reacciones de primer orden
En una reacción de primer orden , la velocidad de reacción es directamente proporcional a la concentración de uno de los reactivos. Las reacciones de primer orden a menudo tienen la forma general A → productos. La velocidad diferencial para una reacción de primer orden es la siguiente:
[ textrm {rate} = – dfrac { Delta [ textrm A]} { Delta t} = k [ textrm A] label {14.4.5} ]
Si la concentración de A se duplica, la velocidad de reacción se duplica; Si la concentración de A aumenta en un factor de 10, la velocidad de reacción aumenta en un factor de 10, y así sucesivamente. Debido a que las unidades de la velocidad de reacción son siempre moles por litro por segundo, las unidades de una constante de velocidad de primer orden son segundos recíprocos (s −1 ).
La ley de velocidad integrada para una reacción de primer orden se puede escribir de dos maneras diferentes: una con exponentes y otra con logaritmos. La forma exponencial es la siguiente:
[[A] = [A] _0e ^ {- kt} label {14.4.6} ]
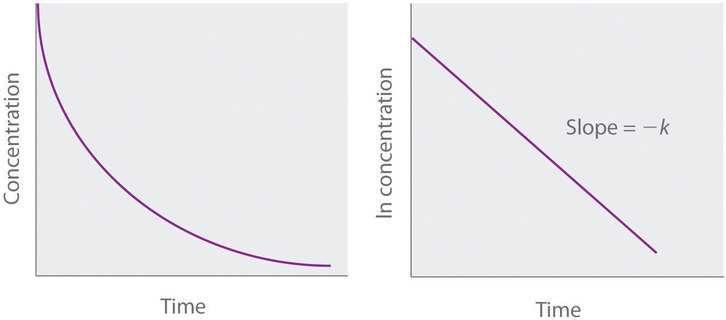
donde [A] 0 es la concentración inicial del reactivo A en t = 0; k es la constante de velocidad; y e es la base de los logaritmos naturales, que tiene el valor 2.718 con tres decimales. Recuerde que una ley de tasa integrada da la relación entre la concentración de reactivo y el tiempo. La ecuación ( ref {14.4.6} ) predice que la concentración de A disminuirá en una curva exponencial suave con el tiempo. Al tomar el logaritmo natural de cada lado de Ecuación ( ref {14.4.6} ) y reorganizar, obtenemos una expresión logarítmica alternativa de la relación entre la concentración de A y t [ 19459022]:
[ ln [A] = ln [A] _0 – kt label {14.4.7} ]
Porque La ecuación ( ref {14.4.7} ) tiene la forma de la ecuación algebraica para una línea recta,
[y = mx + b, ]
con (y = ln [A] ) y (b = ln [A] _0 ), una gráfica de ( ln [A] ) versus (t ) por primera vez -la reacción del orden debe dar una línea recta con una pendiente de (- k ) y una intersección de ( ln [A] _0 ). O la ley de tasa diferencial ( Ecuación ( ref {14.4.5} ) ) o la ley de tasa integrada ( Ecuación ( ref {14.4.7} ) ) puede usarse para determinar si una reacción particular es de primer orden.
Las reacciones de primer orden son muy comunes. Ya hemos encontrado dos ejemplos de reacciones de primer orden: la hidrólisis de la aspirina (Figura ( PageIndex {4} )) y la reacción de t -butilbromuro con agua para dar t -butanol (Ecuación ( ref {14.10} )). Otra reacción que exhibe una cinética aparente de primer orden es la hidrólisis del medicamento contra el cáncer cisplatino.
El cisplatino, el primer medicamento contra el cáncer “inorgánico” que se descubre, es único en su capacidad de causar la remisión completa de los cánceres de órganos reproductores relativamente raros pero mortales en adultos jóvenes. Las estructuras del cisplatino y su producto de hidrólisis son las siguientes:
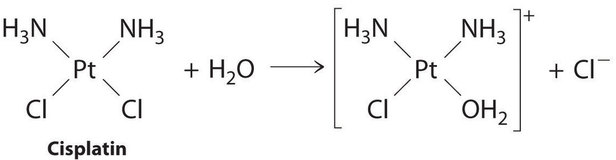
Figura ( PageIndex {5} ): reacción de cis-platino con agua.
Ambos compuestos de platino tienen cuatro grupos dispuestos en un plano cuadrado alrededor de un ion Pt (II). La reacción que se muestra en Figura ( PageIndex {5} ) es importante porque el cisplatino, la forma en que se administra el medicamento, no es la forma en que el medicamento está activo. En cambio, al menos un ion cloruro debe ser reemplazado por agua para producir una especie que reaccione con ácido desoxirribonucleico (ADN) para evitar la división celular y el crecimiento tumoral. En consecuencia, la cinética de la reacción en Figura ( PageIndex {4} ) se ha estudiado ampliamente para encontrar formas de maximizar la concentración de las especies activas.
Si una representación gráfica de la concentración de reactivo frente al tiempo no es lineal, pero una representación gráfica del logaritmo natural de la concentración de reactivo frente al tiempo es lineal, entonces la reacción es de primer orden.
La ley de velocidad y el orden de reacción de la hidrólisis de cisplatino se determinan a partir de datos experimentales, como los que se muestran en Ta ble ( PageIndex {1} ). La tabla enumera los datos de velocidad inicial para cuatro experimentos en los que la reacción se realizó a pH 7,0 y 25 ° C pero con diferentes concentraciones iniciales de cisplatino.
| Experimento | [Cisplatino] 0 (M) | Velocidad inicial (M / min) |
|---|---|---|
| 1 | 0,0060 | 9,0 × 10 −6 |
| 2 | 0,012 | 1,8 × 10 −5 |
| 3 | 0,024 | 3,6 × 10 −5 |
| 4 | 0,030 | 4,5 × 10 −5 |
Debido a que la velocidad de reacción aumenta al aumentar la concentración de cisplatino, sabemos que esta no puede ser una reacción de orden cero. La comparación de los experimentos 1 y 2 en la Tabla ( PageIndex {1} ) muestra que la velocidad de reacción se duplica [(1.8 × 10 −5 M / min) ÷ (9.0 × 10 −6 M / min) = 2.0] cuando la concentración de cisplatino se duplica (de 0.0060 M a 0.012 M). Del mismo modo, la comparación de los Experimentos 1 y 4 muestra que la velocidad de reacción aumenta en un factor de 5 [(4.5 × 10 −5 M / min) ÷ (9.0 × 10 −6 M / min) = 5.0] cuando la concentración de cisplatino se incrementa en un factor de 5 (de 0.0060 M a 0.030 M). Debido a que la velocidad de reacción es directamente proporcional a la concentración del reactivo, el exponente de la concentración de cisplatino en la ley de velocidad debe ser 1, por lo que la ley de velocidad es velocidad = k [cisplatino] 1 [ 19459034]. Así, la reacción es de primer orden. Sabiendo esto, podemos calcular la constante de velocidad usando la ley de velocidad diferencial para una reacción de primer orden y los datos en cualquier fila de la Tabla ( PageIndex {1} ). Por ejemplo, sustituyendo los valores del Experimento 3 en Ecuación ( ref {14.4.5} ) ,
3,6 × 10 −5 M / min = k (0,024 M)
1,5 × 10 −3 min −1 = k
Conocer la constante de velocidad para la hidrólisis de cisplatino y las constantes de velocidad para reacciones posteriores que producen especies que son altamente tóxicas permite a los farmacéuticos del hospital proporcionar a los pacientes soluciones que contienen solo la forma deseada del medicamento.
También podemos usar la ley de velocidad integrada para determinar la velocidad de reacción para la hidrólisis de cisplatino. Para hacer esto, examinamos el cambio en la concentración del reactivo o del producto en función del tiempo a una concentración inicial de cisplatino inicial. La Figura ( PageIndex {6a} ) muestra gráficos para una solución que originalmente contenía cisplatino 0.0100 M y se mantuvo a pH 7 y 25 ° C.
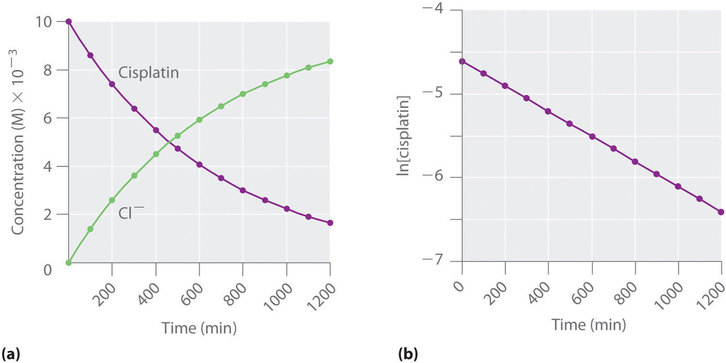
La concentración de cisplatino disminuye suavemente con el tiempo, y la concentración de iones cloruro aumenta de manera similar. Cuando graficamos el logaritmo natural de la concentración de cisplatino versus tiempo, obtenemos la gráfica que se muestra en la parte (b) en Figura ( PageIndex {6} ) . La línea recta es consistente con el comportamiento de un sistema que obedece a una ley de tasa de primer orden. Podemos usar dos puntos en la línea para calcular la pendiente de la línea, lo que nos da la constante de velocidad para la reacción. Tomando así los puntos de la parte (a) en Figura ( PageIndex {6} ) para t = 100 min ([cisplatino] = 0.0086 M) y t = 1000 min ([cisplatino] = 0,0022 M),
[ begin {align} textrm {pendiente} & = dfrac { ln [ textrm {cisplatin}] _ {1000} – ln [ textrm {cisplatin}] _ {100}} { mathrm {1000 ; min-100 ; min}}
\ – k & = dfrac { ln 0.0022- ln 0.0086} { mathrm {1000 ; min-100 ; min}} = dfrac {-6.12 – (- 4.76)} { mathrm {900 ; min}} = – 1.51 times10 ^ {- 3} ; mathrm {min ^ {- 1}}
\ k & = 1.5 veces10 ^ {- 3} ; mathrm {min ^ {- 1}} end {align} ]
La pendiente es negativa porque estamos calculando la tasa de desaparición de cisplatino. Además, la constante de velocidad tiene unidades de min −1 porque los tiempos graficados en los ejes horizontales en las partes (a) y (b) en Figura ( PageIndex {6} ) [19459011 ] son en minutos en lugar de segundos.
El orden de reacción y la magnitud de la constante de velocidad que obtenemos usando la ley de velocidad integrada son exactamente los mismos que calculamos anteriormente usando la ley de velocidad diferencial. Esto debe ser cierto si los experimentos se llevaron a cabo en las mismas condiciones.
Reacciones de segundo orden
El tipo más simple de reacción de segundo orden es aquella cuya velocidad es proporcional al cuadrado de la concentración de un reactivo. Estos generalmente tienen la forma 2A → productos. Un segundo tipo de reacción de segundo orden tiene una velocidad de reacción que es proporcional al producto de las concentraciones de dos reactivos. Tales reacciones generalmente tienen la forma A + B → productos. Un ejemplo de lo primero es una reacción de dimerización, en la que dos moléculas más pequeñas, cada una llamada monómero, se combinan para formar una molécula más grande (un dímero).
La ley de velocidad diferencial para la reacción de segundo orden más simple en la que 2A → productos es la siguiente:
[ textrm {rate} = – dfrac { Delta [ textrm A]} {2 Delta t} = k [ textrm A] ^ 2 label {14.4.8} ]
En consecuencia, duplicando la concentración de A cuadruplica la velocidad de reacción. Para que las unidades de la velocidad de reacción sean moles por litro por segundo (M / s), las unidades de una constante de velocidad de segundo orden deben ser las inversas (M −1 · s −1 ). Debido a que las unidades de molaridad se expresan como mol / L, la unidad de la constante de velocidad también se puede escribir como L (mol · s).
Para los productos de reacción 2A →, la siguiente ley de velocidad integrada describe la concentración del reactivo en un momento dado:
[ dfrac {1} {[ textrm A]} = dfrac {1} {[ textrm A] _0} + kt label {14.4.9} ]
Porque La ecuación ( ref {14.4.9} ) tiene la forma de una ecuación algebraica para una línea recta, y = mx + b , con y = 1 / [A] y b = 1 / [A] 0 , una gráfica de 1 / [ A] versus t para una reacción simple de segundo orden es una línea recta con una pendiente de k y una intersección de 1 / [A] 0 .
Las reacciones de segundo orden generalmente tienen la forma 2A → productos o A + B → productos.
Las reacciones simples de segundo orden son comunes. Además de las reacciones de dimerización, otros dos ejemplos son la descomposición de NO 2 a NO y O 2 y la descomposición de HI a I 2 y H [19459025 ] 2 . La mayoría de los ejemplos involucran moléculas inorgánicas simples, pero también hay ejemplos orgánicos. Podemos seguir el progreso de la reacción descrita en el siguiente párrafo monitoreando la disminución en la intensidad del color rojo de la mezcla de reacción.
Muchos compuestos orgánicos cíclicos que contienen dos dobles enlaces carbono-carbono experimentan una reacción de dimerización para dar estructuras complejas. Un ejemplo es el siguiente:
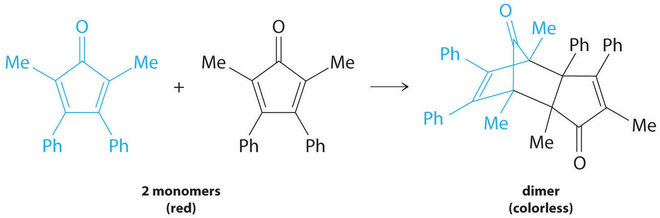
Figura ( PageIndex {7} )
Por simplicidad, nos referiremos a este reactivo y producto como “monómero” y “dímero”, respectivamente. El nombre sistemático del monómero es 2,5-dimetil-3,4-difenilciclopentadienona. El nombre sistemático del dímero es el nombre del monómero seguido de “dímero”. Debido a que los monómeros son iguales, la ecuación general para esta reacción es 2A → producto. Esta reacción representa una clase importante de reacciones orgánicas utilizadas en la industria farmacéutica para preparar esqueletos de carbono complejos para la síntesis de fármacos. Al igual que las reacciones de primer orden estudiadas anteriormente, puede analizarse utilizando la ley de tasa diferencial ( Ecuación ( ref {14.4.8} ) ) o la ley de tasa integrada ( Ecuación ( ref {14.4.9} ) ).
| Tiempo (min) | [Monómero] (M) | Instantaneous Rate (M/min) |
|---|---|---|
| 10 | 0.0044 | 8.0 × 10 −5 |
| 26 | 0.0034 | 5.0 × 10 −5 |
| 44 | 0.0027 | 3.1 × 10 −5 |
| 70 | 0.0020 | 1.8 × 10 −5 |
| 120 | 0.0014 | 8.0 × 10 −6 |
To determine the differential rate law for the reaction, we need data on how the reaction rate varies as a function of monomer concentrations, which are provided in Table (PageIndex{2}) . From the data, we see that the reaction rate is not independent of the monomer concentration, so this is not a zeroth-order reaction. We also see that the reaction rate is not proportional to the monomer concentration, so the reaction is not first order. Comparing the data in the second and fourth rows shows that the reaction rate decreases by a factor of 2.8 when the monomer concentration decreases by a factor of 1.7:
[dfrac{5.0times10^{-5}textrm{ M/min}}{1.8times10^{-5}textrm{ M/min}}=2.8hspace{5mm}textrm{and}hspace{5mm}dfrac{3.4times10^{-3}textrm{ M}}{2.0times10^{-3} textrm{ M}}=1.7]
Because (1.7) 2 = 2.9 ≈ 2.8, the reaction rate is approximately proportional to the square of the monomer concentration.
rate ∝ [monomer] 2
This means that the reaction is second order in the monomer. Using Equation (ref{14.4.8}) and the data from any row in Table (PageIndex{2}) , we can calculate the rate constant. Substituting values at time 10 min, for example, gives the following:
[begin{align}textrm{rate}&=k[textrm A]^2 \8.0times10^{-5}textrm{ M/min}&=k(4.4times10^{-3}textrm{ M})^2 \4.1 textrm{ M}^{-1}cdot textrm{min}^{-1}&=kend{align}]
We can also determine the reaction order using the integrated rate law. To do so, we use the decrease in the concentration of the monomer as a function of time for a single reaction, plotted in Figure (PageIndex{8a}) . The measurements show that the concentration of the monomer (initially 5.4 × 10 −3 M) decreases with increasing time. This graph also shows that the reaction rate decreases smoothly with increasing time. According to the integrated rate law for a second-order reaction, a plot of 1/[monomer] versus t should be a straight line, as shown in Figure (PageIndex{8b}) . Any pair of points on the line can be used to calculate the slope, which is the second-order rate constant. In this example, k = 4.1 M −1 ·min −1 , which is consistent with the result obtained using the differential rate equation. Although in this example the stoichiometric coefficient is the same as the reaction order, this is not always the case. The reaction order must always be determined experimentally.
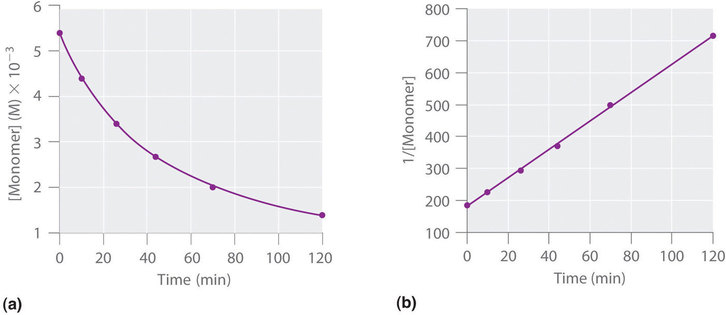
For two or more reactions of the same order, the reaction with the largest rate constant is the fastest. Because the units of the rate constants for zeroth-, first-, and second-order reactions are different, however, we cannot compare the magnitudes of rate constants for reactions that have different orders.
In addition to the simple second-order reaction and rate law we have just described, another very common second-order reaction has the general form (A + B rightarrow products), in which the reaction is first order in (A) and first order in (B). The differential rate law for this reaction is as follows:
[textrm{rate}=-dfrac{Delta[textrm A]}{Delta t}=-dfrac{Delta[textrm B]}{Delta t}=k[textrm A][textrm B] label{14.4.10}]
Because the reaction is first order both in A and in B, it has an overall reaction order of 2. (The integrated rate law for this reaction is rather complex, so we will not describe it.) We can recognize second-order reactions of this sort because the reaction rate is proportional to the concentrations of each reactant.
Summary
The reaction rate of a zeroth-order reaction is independent of the concentration of the reactants. The reaction rate of a first-order reaction is directly proportional to the concentration of one reactant. The reaction rate of a simple second-order reaction is proportional to the square of the concentration of one reactant. Knowing the rate law of a reaction gives clues to the reaction mechanism.
- zeroth-order reaction: [textrm{rate}=-dfrac{Delta[textrm A]}{Delta t}=k
onumber] [[A] = [A]_0 − kt
onumber ] - first-order reaction : [textrm{rate}=-dfrac{Delta[textrm A]}{Delta t}=k[textrm A]
onumber] [[A] = [A]_0e^{−kt}] [ln[A] = ln[A]_0 − kt
onumber ] - second-order reaction: [textrm{rate}=-dfrac{Delta[textrm A]}{Delta t}=k[textrm A]^2
onumber] [dfrac{1}{[textrm A]}=dfrac{1}{[textrm A]_0}+kt
onumber ]