Como aprendió anteriormente, los ácidos y las bases se pueden definir de varias maneras diferentes (Tabla ( PageIndex {1} )). Recuerde que la definición de Arrhenius de un ácido es una sustancia que se disocia en el agua para producir (H ^ + ) iones (protones), y una base de Arrhenius es una sustancia que se disocia en el agua para producir (OH ^ – ) ( hidróxido) iones. Según esta visión, una reacción ácido-base implica la reacción de un protón con un ion hidróxido para formar agua. Aunque Brønsted y Lowry definieron un ácido de manera similar a Arrhenius al describir un ácido como cualquier sustancia que pueda donar un protón, la definición de base de Brønsted-Lowry es mucho más general que la definición de Arrhenius. En términos de Brønsted – Lowry, una base es cualquier sustancia que puede aceptar un protón, por lo que una base no se limita solo a un ion hidróxido. Esto significa que por cada ácido Brønsted – Lowry, existe una base conjugada correspondiente con un protón menos. En consecuencia, todas las reacciones Brønsted – Lowry ácido-base en realidad implican dos pares conjugados de ácido-base y la transferencia de un protón de una sustancia (el ácido) a otra (la base). En contraste, la definición de Lewis de ácidos y bases, se enfoca en aceptar o donar pares de electrones en lugar de protones. Una base de Lewis es un donante de pares de electrones, y un ácido de Lewis es un receptor de pares de electrones.
| Definición | Ácidos | Bases |
|---|---|---|
| Arrhenius | (H ^ + ) donante | Donante (OH ^ – ) |
| Brønsted – Lowry | (H ^ + ) donante | Aceptador (H ^ + ) |
| Lewis | aceptor de pares de electrones | donante de pares de electrones |
Debido a que este capítulo trata los equilibrios ácido-base en solución acuosa, nuestra discusión utilizará principalmente las definiciones y nomenclatura de Brønsted-Lowry. Sin embargo, recuerde que las tres definiciones son solo formas diferentes de ver el mismo tipo de reacción: un protón es un ácido y el ion hidróxido es una base, sin importar qué definición use. En la práctica, los químicos tienden a usar la definición que sea más útil para hacer un punto en particular o comprender un sistema dado. Si, por ejemplo, nos referimos a una base que tiene uno o más pares de electrones solitarios que pueden aceptar un protón, simplemente estamos combinando las definiciones de Lewis y Brønsted-Lowry para enfatizar las propiedades características de una base.
Propiedades ácido-base del agua
Recuerde que debido a su estructura altamente polar, el agua líquida puede actuar como un ácido (al donar un protón a una base) o como una base (al usar un par solitario de electrones para aceptar un protón). Por ejemplo, cuando un ácido fuerte como el HCl se disuelve en agua, se disocia en iones de cloruro ( (Cl ^ – )) y protones ( (H ^ + )). El protón, a su vez, reacciona con una molécula de agua para formar el ion hidronio ( (H_3O ^ + )):
[ underset {acid} {HCl _ {(aq)}} + underset {base} {H_2O _ {(l)}} rightarrow underset {acid} {H_3O ^ + _ {(aq)}} + underset {base} {Cl ^ -_ {(aq)}} label {16.3.1a} ]
En esta reacción, (HCl ) es el ácido, y el agua actúa como base al aceptar un ion (H ^ + ). La reacción en la ecuación ref {16.3.1a} a menudo se escribe en una forma más simple eliminando (H_2O ) de cada lado:
[HCl _ {(aq)} rightarrow H ^ + _ {(aq)} + Cl ^ -_ {(aq)} label {16.3.1b} ]
En la ecuación ref {16.3.1b}, el ion hidronio está representado por (H ^ + ), aunque los iones (H ^ + ) libres no existen en el agua líquida, ya que esta reacción demuestra: [19459010 ]
[H ^ + _ {(aq)} + H_2O _ {(l)} rightarrow H_3O ^ + _ {(aq)} ]
El agua también puede actuar como un ácido, como se muestra en la Ecuación ref {16.3.2}. En esta reacción de equilibrio, (H_2O ) dona un protón a (NH_3 ), que actúa como base:
[ underset {acid} {H_2O _ {(aq)}} + underset {base} {NH_ {3 (aq)}} rightleftharpoons underset {acid} {NH ^ + _ {4 (aq) }} + underset {base} {OH ^ -_ {(aq)}} label {16.3.2} ]
El agua se denomina anfibrótica, lo que significa que puede comportarse como un ácido o una base, dependiendo de la naturaleza del otro reactivo. Observe que la ecuación ( ref {16.3.2} ) es una reacción de equilibrio como lo indica la flecha doble y, por lo tanto, tiene una constante de equilibrio asociada.
La constante del producto iónico del agua líquida
Debido a que el agua es anfibrótica, una molécula de agua puede reaccionar con otra para formar un ion (OH ^ – ) y un ion (H_3O ^ + ) en un proceso de autoionización:
[2H_2O _ {(l)} rightleftharpoons H_3O ^ + _ {(aq)} + OH ^ −_ {(aq)} label {16.3.3} ]
La constante de equilibrio (K ) para esta reacción se puede escribir de la siguiente manera:
[K_ {a} = dfrac {a_ {H_3O ^ +} · a_ {OH ^ -}} {a_ {H_2O} ^ 2} aprox frac {[H_ {3} O ^ {+} ] [HO ^ {-}]} {(1) ^ {2}} = [H_ {3} O ^ {+}] [HO ^ {-}] label {16.3.4} ]
donde (a ) es la actividad de una especie. Como el agua es el disolvente y se supone que la solución es diluida, la actividad del agua se aproxima por la actividad del agua pura, que se define como que tiene un valor de 1. La actividad de cada soluto se aproxima por la molaridad de El soluto. En esta reacción, una molécula de agua actúa como un ácido y una molécula de agua actúa como una base. Por lo tanto, esta reacción en realidad se puede designar como (K_a ) del agua y como (K_b ) del agua. Sin embargo, es más común designar esta reacción y la ley de acción de masas asociada como la (K_w ) del agua:
[K_ {w} = [H_ {3} O ^ {+}] [HO ^ {-}] label {16.3.5} ]
Cuando el agua líquida pura está en equilibrio con los iones hidronio e hidróxido a 25 ° C, las concentraciones del ion hidronio y el ion hidróxido son iguales:
[[H_3O ^ +] = [OH ^ -] = 1.003 por 10 ^ {- 7} ; M label {16.3.6} ]
Por lo tanto, el número de moléculas de agua disociadas es muy pequeño, aproximadamente 2 ppb.
Sustituyendo los valores para ([H_3O ^ +] ) y ([OH ^ -] ) a 25 ° C en esta expresión
[K_w = (1.003 times10 ^ {- 7}) (1.003 times 10 ^ {- 7}) = 1.006 times 10 ^ {- 14} label {16.3.7} ]
Así, a tres cifras significativas, (K_w = 1.01 times 10 ^ {- 14} ) a temperatura ambiente, y [K_w = 1.01 times 10 ^ {- 14} = [H_3O ^ +] [OH ^ -] label {16.3.7b} ].
Como cualquier otra constante de equilibrio, (K_w ) varía con la temperatura, desde (1.15 veces 10 ^ {- 15} ) a 0 ° C hasta (4.99 veces 10 ^ {- 13} ) a 100 ° C.
En agua pura, las concentraciones del ion hidronio y el ion hidróxido son iguales y, por lo tanto, la solución es neutra. Si ([H_3O ^ +]> [OH ^ -] ), sin embargo, la solución es ácida, mientras que si ([H_3O ^ +] <[OH ^ -] ), la solución es básica. Para una solución acuosa, la concentración de (H_3O ^ + ) es una medida cuantitativa de la acidez: cuanto mayor es la concentración de (H_3O ^ + ), más ácida es la solución. Por el contrario, cuanto mayor sea la concentración de (OH ^ - ), más básica será la solución. En la mayoría de las situaciones que encontrará, las concentraciones de (H_3O ^ + ) y (OH ^ - ) de la disociación del agua son tan pequeñas ( (1.003 times 10 ^ {- 7} M )) que pueden ignorarse al calcular las concentraciones de (H_3O ^ + ) u (OH ^ - ) de soluciones de ácidos y bases, pero este no es siempre el caso.
La relación entre pH, pOH y (pK_w )
La escala de pH es una forma concisa de describir la concentración de (H_3O ^ + ) y, por lo tanto, la acidez o basicidad de una solución. Recuerde que el pH y la concentración de (H ^ + ) ( (H_3O ^ + )) están relacionados de la siguiente manera:
[pH = – log_ {10} [H ^ +] label {16.3.8} ]
[[H ^ +] = 10 ^ {- pH} label {16.3.9} ]
Debido a que la escala es logarítmica, una diferencia de pH de 1 entre dos soluciones corresponde a una diferencia de un factor de 10 en sus concentraciones de iones hidronio. Recuerde también que el pH de una solución neutra es 7.00 ( ([H_3O ^ +] = 1.0 times 10 ^ {- 7} ; M )), mientras que las soluciones ácidas tienen un pH <7.00 (correspondiente a ([H_3O ^ +]> 1.0 times 10 ^ {- 7} )) y las soluciones básicas tienen pH> 7.00 (correspondiente a ([H_3O ^ +] <1.0 times 10 ^ {- 7} )).
Se utilizan sistemas de notación similares para describir muchas otras cantidades químicas que contienen un gran exponente negativo. Por ejemplo, los químicos usan una escala de pOH análoga para describir la concentración de iones hidróxido de una solución. El pOH y ([OH ^ -] ) están relacionados de la siguiente manera:
[pOH = – log_ {10} [OH ^ -] label {16.3.10} ]
[[OH ^ -] = 10 ^ {- pOH} label {16.3.11} ]
La constante (K_w ) también se puede expresar usando esta notación, donde (pK_w = – log ; K_w ).
Debido a que una solución neutral tiene ([OH ^ -] = 1.0 times 10 ^ {- 7} ), el pOH de una solución neutral es 7.00. En consecuencia, la suma del pH y el pOH para una solución neutra a 25 ° C es 7.00 + 7.00 = 14.00. Podemos demostrar que la suma de pH y pOH es igual a 14.00 para cualquier solución acuosa a 25 ° C tomando el logaritmo negativo de ambos lados de la ecuación ref {16.3.6b}:
[ begin {align} – log_ {10} K_w & = pK_w \ [4pt] & = – log ([H_3O ^ {+}] [OH ^ {-}]) \ [4pt ] & = (- log [H_3O ^ {+}]) + (- log [OH ^ {-}]) \ [4pt] & = pH + pOH label {16.3.12} end {align} ]
Así, a cualquier temperatura, (pH + pOH = pK_w ), entonces a 25 ° C, donde (K_w = 1.0 times 10 ^ {- 14} ), pH + pOH = 14.00. De manera más general, el pH de cualquier solución neutra es la mitad del (pK_w ) a esa temperatura. La relación entre pH, pOH y la acidez o basicidad de una solución se resume gráficamente en la Figura ( PageIndex {1} ) sobre el rango de pH común de 0 a 14. Observe la relación inversa entre las escalas de pH y pOH.
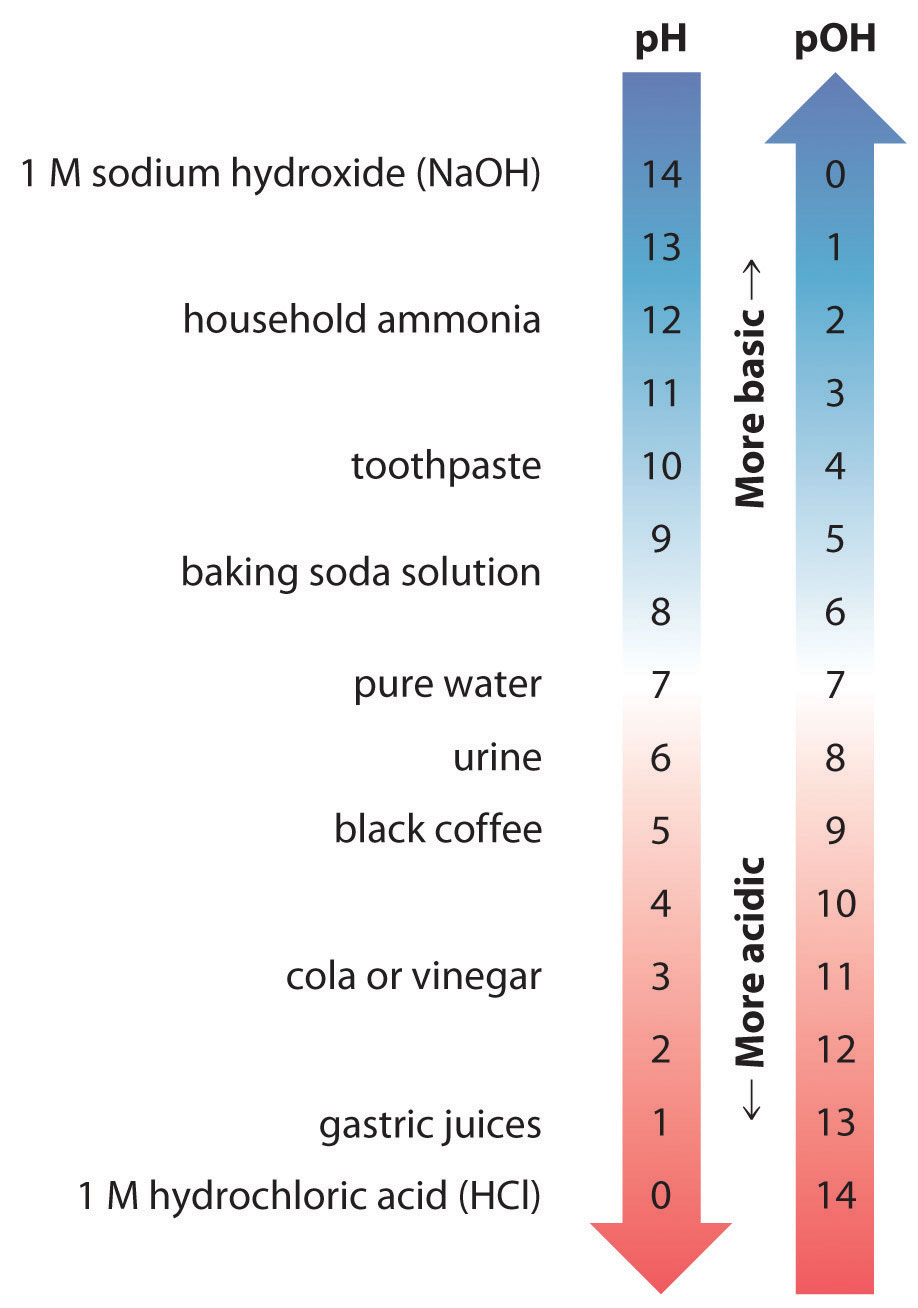
Para cualquier solución neutra, pH + pOH = 14.00 (a 25 ° C) con pH = pOH = 7.
Resumen
El agua es anfibrótica: puede actuar como un ácido al donar un protón a una base para formar el ion hidróxido, o como una base al aceptar un protón de un ácido para formar el ion hidronio ( (H_3O ^ + ) ) La autoionización del agua líquida produce iones (OH ^ – ) y (H_3O ^ + ). La constante de equilibrio para esta reacción se llama constante del producto iónico del agua líquida (Kw) y se define como (K_w = [H_3O ^ +] [OH ^ -] ). A 25 ° C, (K_w ) es (1.01 veces 10 ^ {- 14} ); por lo tanto (pH + pOH = pK_w = 14.00 ).
- Para cualquier solución neutra, (pH + pOH = 14.00 ) (a 25 ° C) y (pH = 1/2 pK_w ).
- Constante de producto iónico de agua líquida: [K_w = [H_3O ^ +] [OH ^ -]
onumber ] - Definición de (pH ): [pH = – log10 [H ^ +]
onumber ] o [[H ^ +] = 10 ^ {- pH}
onumber ] - Definición de (pOH ): [pOH = – log_ {10} [OH ^ +]
onumber ] o [[OH ^ -] = 10 ^ {- pOH}
onumber ] - Relación entre (pH ), (pOH ) y (pK_w ): [pK_w = pH + pOH
onumber ]