Debido a su naturaleza anfótera (es decir, actúa como un ácido o una base), el agua no siempre permanece como moléculas (H_2O ). De hecho, dos moléculas de agua reaccionan para formar iones hidronio e hidróxido:
Esto también se llama autoionización del agua. La concentración de (H_3O ^ + ) y (OH ^ – ) son iguales en agua pura debido a la relación estequiométrica 1: 1 de la ecuación 1. La molaridad de H 3 O + y OH – en agua también están ambos (1.0 times 10 ^ {- 7} , M ) a 25 ° C. Por lo tanto, una constante de agua ( (K_w )) se crea para mostrar la condición de equilibrio para la autoionización del agua. El producto de la molaridad del ion hidronio e hidróxido es siempre (1.0 veces 10 ^ {- 14} ).
Estas ecuaciones también se aplican a todas las soluciones acuosas. Sin embargo, (K_w ) cambia a diferentes temperaturas, lo que afecta el rango de pH que se analiza a continuación.
pH y pOH
La constante del agua determina el rango de la escala de pH. Para entender qué es el pK w , es importante entender primero lo que significa “p” en pOH y pH. El bioquímico danés Søren Sørenson propuso el término pH para referirse al “potencial del ion hidrógeno”. Definió la “p” como el negativo del logaritmo, -log, de [H + ]. Por lo tanto, el pH es el logaritmo negativo de la molaridad de H. El pOH es el logaritmo negativo de la molaridad de OH – y el pK w es el negativo logaritmo de la constante del agua. Estas definiciones dan las siguientes ecuaciones:
[pH = – log [H ^ +] label {4a} ]
[pOH = – log [OH ^ -] label {4b} ]
[pK_w = – log [K_w] label {4c} ]
A temperatura ambiente (25 ° C),
[K_w = 1.0 times 10 ^ {- 14} label {4d} ]
Entonces
[pK_w = – log [1.0 times 10 ^ {- 14}] label {4e} ]
Utilizando las propiedades de los logaritmos, la ecuación ( ref {4e} ) puede reescribirse como
[10 ^ {- pK_w} = 10 ^ {- 14}. label {4f} ]
Al sustituir, vemos th en pK w es 14. La ecuación también muestra que cada unidad creciente en la escala disminuye en un factor de diez en la concentración de (H ^ + ). Por ejemplo, un pH de 1 tiene una molaridad diez veces más concentrada que una solución de pH 2.
Desde
[pK_w = 14 label {5a} ]
[pK_w = pH + pOH = 14 etiqueta {5b} ]
Dado que la constante de autoionización (K_w ) depende de la temperatura, estas correlaciones entre los valores de pH y los adjetivos ácidos / neutros / básicos serán diferentes a temperaturas diferentes a 25 ° C. Por ejemplo, la molaridad de hidronio del agua pura a 80 ° C es 4.9 × 10 −7 M , que corresponde a los valores de pH y pOH de:
[ mathrm {pH = – log [H_3O ^ +] = – log (4.9 times 10 ^ {- 7}) = 6.31} label {12} ]
[ mathrm {pOH = – log [OH ^ -] = – log (4.9 times 10 ^ {- 7}) = 6.31} label {13} ]
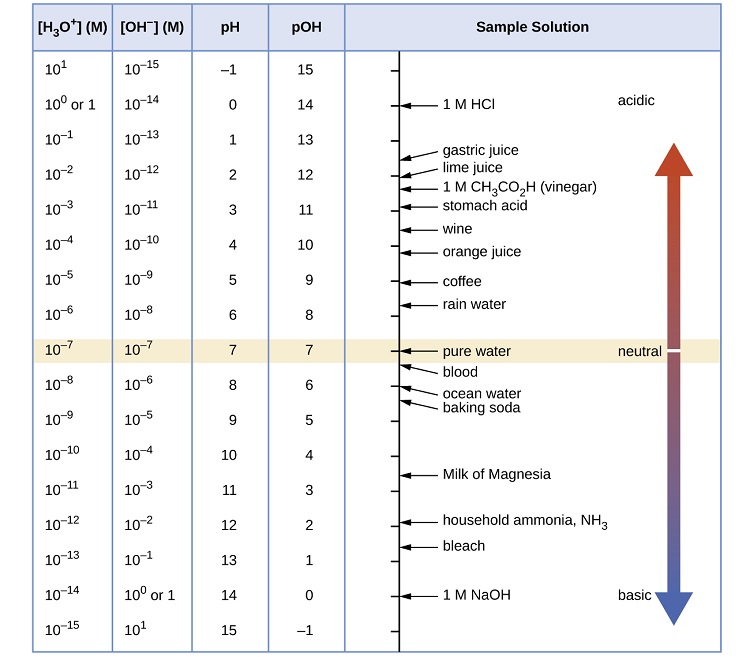
A esta temperatura, entonces, las soluciones neutras exhiben pH = pOH = 6.31, las soluciones ácidas exhiben un pH menor que 6.31 y pOH mayor que 6.31, mientras que las soluciones básicas exhiben pH mayor que 6.31 y pOH menor que 6.31. Esta distinción puede ser importante cuando se estudian ciertos procesos que ocurren a temperaturas no estándar, como las reacciones enzimáticas en organismos de sangre caliente. A menos que se indique lo contrario, se supone que las referencias a los valores de pH son aquellas a temperatura estándar (25 ° C) (Tabla ( PageIndex {1} )).
La escala de pH es logarítmica, lo que significa que un aumento o disminución de un valor entero cambia la concentración en diez veces. Por ejemplo, un pH de 3 es diez veces más ácido que un pH de 4. Asimismo, un pH de 3 es cien veces más ácido que un pH de 5. De manera similar, un pH de 11 es diez veces más básico que un pH de 10.
La Figura ( PageIndex {1} ) representa la escala de pH con soluciones comunes y dónde están en la escala.