En una titulación ácido-base, se utiliza una bureta para administrar volúmenes medidos de una solución de ácido o base de concentración conocida (el titulador) a un matraz que contiene una solución de una base o un ácido, respectivamente, de concentración desconocida (lo desconocido). Si se conoce la concentración del valorante, entonces se puede determinar la concentración de lo desconocido. La siguiente discusión se enfoca en los cambios de pH que ocurren durante una titulación ácido-base. El trazado del pH de la solución en el matraz contra la cantidad de ácido o base añadida produce una curva de titulación. La forma de la curva proporciona información importante sobre lo que ocurre en la solución durante la valoración.
Titulaciones de ácidos y bases fuertes
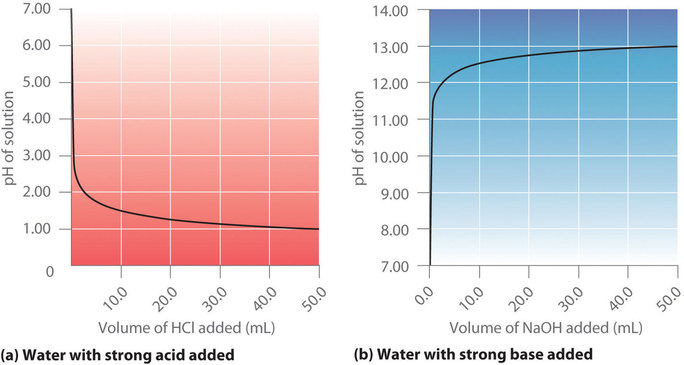
La Figura ( PageIndex {1a} ) muestra un gráfico del pH a medida que se agrega gradualmente HCl 0,20 M a 50,00 ml de agua pura. El pH de la muestra en el matraz es inicialmente de 7.00 (como se esperaba para el agua pura), pero cae muy rápidamente a medida que se agrega HCl. Finalmente, el pH se vuelve constante a 0.70, un punto muy por encima de su valor de 1.00 con la adición de 50.0 mL de HCl (0.70 es el pH de 0.20 M HCl). En contraste, cuando se agregan 0.20 M (NaOH ) a 50.00 mL de agua destilada, el pH (inicialmente 7.00) sube muy rápidamente al principio, pero luego más gradualmente, llegando a un límite de 13.30 (el pH de 0.20 M NaOH) , nuevamente más allá de su valor de 13.00 con la adición de 50.0 mL de (NaOH ) como se muestra en la Figura ( PageIndex {1b} ). Como puede ver en estos gráficos, la curva de titulación para agregar una base es la imagen especular de la curva para agregar un ácido.
Suponga que ahora agregamos 0.20 M (NaOH ) a 50.0 mL de una solución 0.10 M de HCl. Debido a que el HCl es un ácido fuerte que está completamente ionizado en agua, la ([H ^ +] ) inicial es de 0,10 M y el pH inicial es de 1,00. Agregar (NaOH ) disminuye la concentración de H + debido a la reacción de neutralización: ( (OH ^ – + H ^ + rightleftharpoons H_2O )) (en la parte (a) en la Figura ( PageIndex {2} ) ) Por lo tanto, el pH de la solución aumenta gradualmente. Sin embargo, cerca del punto de equivalencia, el punto en el que el número de moles de base (o ácido) agregado es igual al número de moles de ácido (o base) originalmente presentes en la solución, el pH aumenta mucho más rápidamente porque la mayor parte del H + Los iones originalmente presentes se han consumido. Para la valoración de un ácido fuerte monoprótico (HCl) con una base fuerte monobásica (NaOH), podemos calcular el volumen de base necesario para alcanzar el punto de equivalencia a partir de la siguiente relación:
[moles ; of ; base = (volume) _b (molarity) _bV_bM_b = moles ; of ; acid = (volume) _a (molarity) _a = V_aM_a label {Eq1} ]
Si se agregan 0,20 M (NaOH ) a 50,0 ml de una solución de HCl 0,10 M, resolvemos (V_b ):
[V_b (0,20 Me) = 0,025 L = 25 ml ]
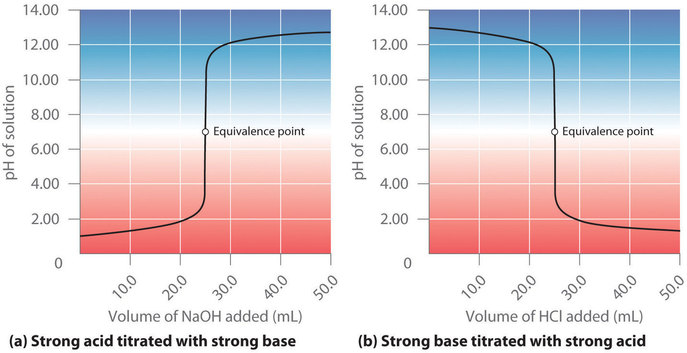
En el punto de equivalencia (cuando se han agregado 25,0 ml de solución (NaOH )), se completa la neutralización: solo queda una sal en solución (NaCl) y el pH de la solución es 7,00. Agregar más (NaOH ) produce un rápido aumento del pH, pero finalmente el pH se nivela a un valor de aproximadamente 13,30, el pH de 0,20 M (NaOH ).
Como se muestra en la Figura ( PageIndex {2b} ), la titulación de 50.0 mL de una solución 0.10 M de ( ce {NaOH} ) con 0.20 M ( ce {HCl} ) produce una curva de titulación que es casi la imagen especular de la curva de titulación en la Figura ( PageIndex {2a} ). El pH es inicialmente 13.00, y disminuye lentamente a medida que se agrega ( ce {HCl} ). A medida que se acerca al punto de equivalencia, el pH cae rápidamente antes de estabilizarse a un valor de aproximadamente 0,70, el pH de HCl 0,20 M.
La titulación de un ácido fuerte con una base fuerte o una base fuerte con un ácido fuerte produce una curva en forma de S. La curva es algo asimétrica porque el aumento constante en el volumen de la solución durante la titulación hace que la solución se vuelva más diluida. Debido al efecto de nivelación, la forma de la curva para una titulación que involucra un ácido fuerte y una base fuerte depende solo de las concentraciones del ácido y la base, no de sus identidades.
Titulaciones de ácidos y bases débiles
A diferencia de los ácidos y bases fuertes, la forma de la curva de titulación para un ácido débil o una base débil depende dramáticamente de la identidad del ácido o la base y la correspondiente (K_a ) o (K_b ) . Como veremos, el pH también cambia mucho más gradualmente alrededor del punto de equivalencia en la valoración de un ácido débil o una base débil. Como aprendió anteriormente, ([H ^ +] ) de una solución de un ácido débil (HA) no es igual a la concentración del ácido, sino que depende tanto de su (pK_a ) como de su concentración. Debido a que solo una fracción de un ácido débil se disocia, ([H ^ +] ) es menor que ([HA] ). Por lo tanto, el pH de una solución de un ácido débil es mayor que el pH de una solución de un ácido fuerte de la misma concentración. La Figura ( PageIndex {3a} ) muestra la curva de titulación para 50.0 mL de una solución de ácido acético 0.100 M con 0.200 M (NaOH ) superpuesta en la curva para la titulación de HCl 0.100 M que se muestra en la parte (a) en la Figura ( PageIndex {2} ). Debajo del punto de equivalencia, las dos curvas son muy diferentes. Antes de agregar cualquier base, el pH de la solución de ácido acético es mayor que el pH de la solución de HCl, y el pH cambia más rápidamente durante la primera parte de la valoración. Tenga en cuenta también que el pH de la solución de ácido acético en el punto de equivalencia es mayor que 7.00. Es decir, en el punto de equivalencia, la solución es básica. Además, el cambio en el pH alrededor del punto de equivalencia es solo aproximadamente la mitad de grande que para la titulación de HCl; La magnitud del cambio de pH en el punto de equivalencia depende de la (pK_a ) del ácido que se está titulando. Por encima del punto de equivalencia, sin embargo, las dos curvas son idénticas. Una vez que el ácido ha sido neutralizado, el pH de la solución se controla solo por la cantidad de exceso (NaOH ) presente, independientemente de si el ácido es débil o fuerte.
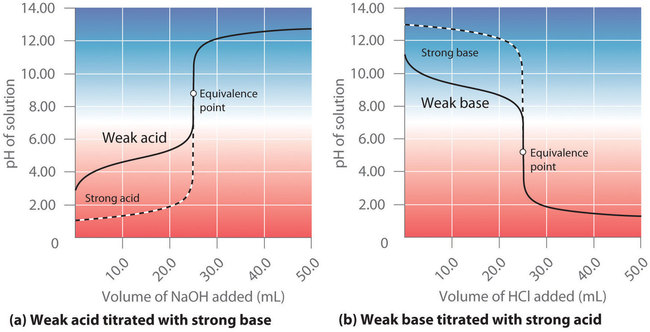
La curva de titulación en la Figura ( PageIndex {3a} ) se creó calculando el pH inicial de la solución de ácido acético antes de agregar cualquier (NaOH ) y luego calculando el pH de la solución después de agregar volúmenes crecientes de (NaOH ). El procedimiento se ilustra en la siguiente subsección y en el Ejemplo ( PageIndex {2} ) para tres puntos en la curva de titulación, usando (pK_a ) de ácido acético (4.76 a 25 ° C; (K_a = 1.7 multiplicado por 10 ^ {- 5} ).
Cálculo del pH de una solución de un ácido débil o una base débil
Como se explicó anteriormente, si conocemos (K_a ) o (K_b ) y la concentración inicial de un ácido débil o una base débil, podemos calcular el pH de una solución de un ácido débil o una base débil estableciendo una tabla ICE (es decir, concentraciones iniciales, cambios en las concentraciones y concentraciones finales). En esta situación, la concentración inicial de ácido acético es 0.100 M. Si definimos (x ) como ([ ce {H ^ {+}}] ) debido a la disociación del ácido, entonces la tabla de Las concentraciones para la ionización de ácido acético 0.100 M son las siguientes:
[CH_3CO_2H _ {(aq)} rightleftharpoons H ^ + _ {(aq)} + CH_3CO_2 ^ – ]
| ICE | ([CH_3CO_2H] ) | ([H ^ +] ) | ([CH_3CO_2 ^ -] ) |
|---|---|---|---|
| inicial | 0.100 | (1,00 por 10 ^ {- 7} ) | 0 |
| cambio | −x | + x | + x |
| final | 0.100 – x | x | x |
En este y en todos los ejemplos posteriores, ignoraremos ([H ^ +] ) y ([OH ^ -] ) debido a la autoionización del agua al calcular la concentración final. Sin embargo, debe usar la Ecuación 16.45 y la Ecuación 16.46 para verificar que esta suposición esté justificada.
Insertando las expresiones para las concentraciones finales en la ecuación de equilibrio (y usando aproximaciones),
[K_a = dfrac {[H ^ +] [CH_3CO_2 ^ -]} {[CH_3CO_2H]} = dfrac {(x) (x)} {0.100 – x} approx dfrac {x ^ 2 } {0.100} = 1.74 veces 10 ^ {- 5} ]
Resolver esta ecuación da (x = [H ^ +] = 1.32 times 10 ^ {- 3} ; M ). Así, el pH de una solución de ácido acético 0.100 M es el siguiente:
[pH = – log (1.32 veces 10 ^ {- 3}) = 2.879 ]
Cálculo del pH durante la valoración de un ácido débil o una base débil
Ahora considere lo que sucede cuando agregamos 5.00 mL de 0.200 M (NaOH ) a 50.00 mL de 0.100 M (CH_3CO_2H ) (parte (a) en la Figura ( PageIndex {3} )). Debido a que la reacción de neutralización se completa, todos los iones (OH ^ – ) agregados reaccionarán con el ácido acético para generar iones acetato y agua:
[CH_3CO_2H _ {(aq)} + OH ^ -_ {(aq)} rightarrow CH_3CO ^ -_ {2 ; (aq)} + H_2O _ {(l)} label {Eq2} ] [ 19459012]
Todos los problemas de este tipo deben resolverse en dos pasos: un cálculo estequiométrico seguido de un cálculo de equilibrio. En el primer paso, usamos la estequiometría de la reacción de neutralización para calcular las cantidades de ácido y base conjugada presentes en la solución después de que se haya producido la reacción de neutralización. En el segundo paso, usamos la ecuación de equilibrio para determinar ([ ( ce {H ^ {+}}] ) de la solución resultante.
Paso 1
Para determinar la cantidad de ácido y base conjugada en solución después de la reacción de neutralización, calculamos la cantidad de ( ce {CH_3CO_2H} ) en la solución original y la cantidad de ( ce {OH ^ {- }} ) en la solución ( ce {NaOH} ) que se agregó. La solución de ácido acético contenía
[50.00 ; cancel {mL} (0.100 ; mmol ( ce {CH_3CO_2H}) / cancel {mL}) = 5.00 ; mmol ( ce {CH_3CO_2H}) ]
La solución ( ce {NaOH} ) contenía
5,00 ml = 1,00 mmol (NaOH )
La comparación de las cantidades muestra que (CH_3CO_2H ) está en exceso. Dado que (OH ^ – ) reacciona con (CH_3CO_2H ) en una estequiometría 1: 1, la cantidad de exceso (CH_3CO_2H ) es la siguiente:
5.00 mmol (CH_3CO_2H ) – 1.00 mmol (OH ^ – ) = 4.00 mmol (CH_3CO_2H )
Cada 1 mmol de (OH ^ – ) reacciona para producir 1 mmol de acetato de iones, por lo que la cantidad final de (CH_3CO_2 ^ – ) es 1,00 mmol.
La estequiometría de la reacción se resume en la siguiente tabla, que muestra el número de moles de las diversas especies, no sus concentraciones.
[ ce {CH3CO2H (aq) + OH ^ {-} (aq) <=> CH3CO2 ^ {-} (aq) + H2O (l)} ]
| ICE | ([ ce {CH_3CO_2H}] ) | ([ ce {OH ^ {-}}] ) | ([ ce {CH_3CO_2 ^ {-}}] ) |
|---|---|---|---|
| inicial | 5,00 mmol | 1,00 mmol | 0 mmol |
| cambio | −1,00 mmol | −1,00 mmol | +1,00 mmol |
| final | 4,00 mmol | 0 mmol | 1,00 mmol |
Esta tabla de ICE proporciona la cantidad inicial de acetato y la cantidad final de (OH ^ – ) iones como 0. Debido a que una solución acuosa de ácido acético siempre contiene al menos una pequeña cantidad de ión acetato en equilibrio con ácido acético , sin embargo, la concentración inicial de acetato no es en realidad 0. El valor puede ignorarse en este cálculo porque la cantidad de (CH_3CO_2 ^ – ) en equilibrio es insignificante en comparación con la cantidad de (OH ^ – ) añadida. Además, debido a la autoionización del agua, ninguna solución acuosa puede contener 0 mmol de (OH ^ – ), pero la cantidad de (OH ^ – ) debido a la autoionización del agua es insignificante en comparación con la cantidad de (OH ^ – ) agregado. Utilizamos las cantidades iniciales de los reactivos para determinar la estequiometría de la reacción y diferir la consideración del equilibrio hasta la segunda mitad del problema.
Paso 2
Para calcular ([ ce {H ^ {+}}] ) en equilibrio después de la adición de (NaOH ), primero debemos calcular [ ( ce {CH_3CO_2H} )] y ( [ ce {CH3CO2 ^ {-}}] ) usando el número de milimoles de cada uno y el volumen total de la solución en este punto de la valoración:
[final ; volumen = 50.00 ; mL + 5.00 ; mL = 55.00 ; mL ] [ left [CH_ {3} CO_ {2} H right] = dfrac {4.00 ; mmol ; CH_ {3} CO_ {2} H} {55.00 ; mL} = 7.27 times 10 ^ {- 2} ; M ] [ left [CH_ {3} CO_ {2} ^ {-} right] = dfrac {1.00 ; mmol ; CH_ {3} CO_ {2} ^ {-}} {55.00 ; mL} = 1.82 veces 10 ^ {- 2} ; M ]
Conociendo las concentraciones de ácido acético e ión acetato en equilibrio y (K_a ) para el ácido acético ( (1.74 times 10 ^ {- 5} )), podemos calcular ([H ^ +] ) en equilibrio:
[K_ {a} = dfrac { left [CH_ {3} CO_ {2} ^ {-} right] left [H ^ {+} right]} { left [CH_ {3 } CO_ {2} H derecha]} ]
[ left [H ^ {+} right] = dfrac {K_ {a} left [CH_ {3} CO_ {2} H right]} { left [CH_ {3} CO_ { 2} ^ {-} right]} = dfrac { left (1.72 times 10 ^ {- 5} right) left (7.27 times 10 ^ {- 2} ; M right)} { left (1.82 times 10 ^ {- 2} right)} = 6.95 times 10 ^ {- 5} ; M ]
Calculando (- log [ ce {H ^ {+}}] ) da
[pH = – log (6.95 veces 10 ^ {- 5}) = 4.158. ]
Al comparar las curvas de titulación para HCl y ácido acético en la Figura ( PageIndex {3a} ), vemos que al agregar la misma cantidad (5.00 mL) de 0.200 M (NaOH ) a 50 mL de 0.100 M La solución de ambos ácidos causa un cambio de pH mucho menor para el HCl (de 1.00 a 1.14) que para el ácido acético (2.88 a 4.16). Esto es consistente con la descripción cualitativa de las formas de las curvas de titulación al comienzo de esta sección. En el Ejemplo ( PageIndex {2} ), calculamos otro punto para construir la curva de titulación del ácido acético.
Como se muestra en la parte (b) en la Figura ( PageIndex {3} ), la curva de titulación para NH3, una base débil, es el reverso de la curva de titulación para el ácido acético. En particular, el pH en el punto de equivalencia en la titulación de una base débil es inferior a 7.00 porque la titulación produce un ácido.
La identidad del ácido débil o la base débil que se está titulando afecta fuertemente la forma de la curva de titulación. La figura ( PageIndex {4} ) ilustra la forma de las curvas de titulación en función de (pK_a ) o (pK_b ). A medida que el ácido o la base que se está titulando se debilita (su (pK_a ) o (pK_b ) se hace más grande), el cambio de pH alrededor del punto de equivalencia disminuye significativamente. Con soluciones muy diluidas, la curva se vuelve tan superficial que ya no se puede usar para determinar el punto de equivalencia.
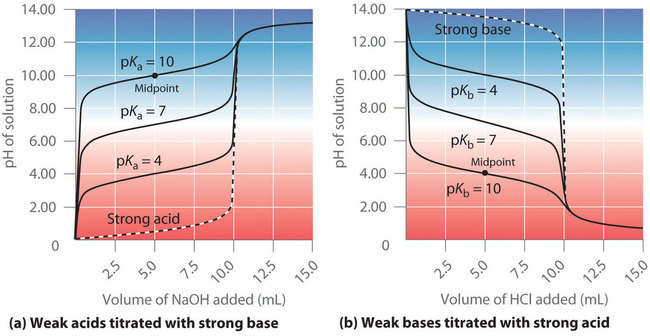
Un punto en la titulación de un ácido débil o una base débil es particularmente importante: el punto medio de una titulación se define como el punto en el que se ha agregado exactamente suficiente ácido (o base) para neutralizar la mitad del ácido (o la base) originalmente presente y ocurre a medio camino del punto de equivalencia. El punto medio se indica en las Figuras ( PageIndex {4a} ) y ( PageIndex {4b} ) para las dos curvas más superficiales. Por definición, en el punto medio de la titulación de un ácido, [HA] = [A−]. Recuerde que la constante de ionización para un ácido débil es la siguiente:
[K_a = dfrac {[H_3O ^ +] [A ^ -]} {[HA]} ]
Si ([HA] = [A ^ -] ), esto se reduce a (K_a = [H_3O ^ +] ). Tomando el logaritmo negativo de ambos lados,
[- log K_a = – log [H_3O +] ]
De las definiciones de (pK_a ) y pH, vemos que esto es idéntico a
[pK_a = pH etiqueta {16.52} ]
Por lo tanto, el pH en el punto medio de la titulación de un ácido débil es igual a (pK_a ) del ácido débil, como se indica en la parte (a) en la Figura ( PageIndex {4} ) para el ácido más débil donde vemos que el punto medio para (pK_a ) = 10 ocurre a pH = 10. Por lo tanto, los métodos de titulación pueden usarse para determinar tanto la concentración como el (pK_a ) (o el (pK_b )) de un ácido débil (o una base débil).
Titulaciones de ácidos o bases polipróticos
Cuando se agrega una base fuerte a una solución de un ácido poliprótico, la reacción de neutralización ocurre en etapas. El grupo más ácido se titula primero, seguido del siguiente más ácido, y así sucesivamente. Si los valores de (pK_a ) están separados por al menos tres unidades de (pK_a ), entonces la curva de titulación general muestra “pasos” bien resueltos correspondientes a la titulación de cada protón. En la Figura ( PageIndex {5} ) se ilustra una titulación del ácido triprótico (H_3PO_4 ) con (NaOH ) y muestra dos pasos bien definidos: el primer punto medio corresponde a (pK_a ) 1, y el segundo punto medio corresponde a (pK_a ) 2 . Debido a que HPO 4 2− es un ácido tan débil, (pK_a ) 3 tiene un valor tan alto que el tercer paso no puede resolverse usando 0.100 M (NaOH ) como titulante.

La curva de titulación para la reacción de una base poliprótica con un ácido fuerte es la imagen especular de la curva que se muestra en la Figura ( PageIndex {5} ). El pH inicial es alto, pero a medida que se agrega ácido, el pH disminuye en pasos si los valores sucesivos (pK_b ) están bien separados. La Tabla E1 enumera las constantes de ionización y los valores (pK_a ) para algunos ácidos y bases polipróticos comunes.
So
[ pH = -logleft [ H^{+} right ]= -logleft ( 3.7 times 10^{-4} right )= 3.43 ]
This answer makes chemical sense because the pH is between the first and second (pK_a) values of oxalic acid, as it must be. We added enough hydroxide ion to completely titrate the first, more acidic proton (which should give us a pH greater than (pK_{a1})), but we added only enough to titrate less than half of the second, less acidic proton, with (pK_{a2}). If we had added exactly enough hydroxide to completely titrate the first proton plus half of the second, we would be at the midpoint of the second step in the titration, and the pH would be 3.81, equal to (pK_{a2}).
Indicators
In practice, most acid–base titrations are not monitored by recording the pH as a function of the amount of the strong acid or base solution used as the titrant. Instead, an acid–base indicator is often used that, if carefully selected, undergoes a dramatic color change at the pH corresponding to the equivalence point of the titration. Indicators are weak acids or bases that exhibit intense colors that vary with pH. The conjugate acid and conjugate base of a good indicator have very different colors so that they can be distinguished easily. Some indicators are colorless in the conjugate acid form but intensely colored when deprotonated (phenolphthalein, for example), which makes them particularly useful.
We can describe the chemistry of indicators by the following general equation:
[ HInleft ( aq right ) rightleftharpoons H^{+}left ( aq right ) + In^{-}left ( aq right )]
where the protonated form is designated by HIn and the conjugate base by (In^−). The ionization constant for the deprotonation of indicator (HIn) is as follows:
[ K_{In} =dfrac{left [ H^{+} right ]left [ In^{-} right ]}{HIn} label{Eq3}]
The (pK_{in}) (its (pK_a)) determines the pH at which the indicator changes color.
Many different substances can be used as indicators, depending on the particular reaction to be monitored. For example, red cabbage juice contains a mixture of colored substances that change from deep red at low pH to light blue at intermediate pH to yellow at high pH (Figure (PageIndex{6})). In all cases, though, a good indicator must have the following properties:
- The color change must be easily detected.
- The color change must be rapid.
- The indicator molecule must not react with the substance being titrated.
- To minimize errors, the indicator should have a pKin that is within one pH unit of the expected pH at the equivalence point of the titration.

Red cabbage juice contains a mixture of substances whose color depends on the pH. Each test tube contains a solution of red cabbage juice in water, but the pH of the solutions varies from pH = 2.0 (far left) to pH = 11.0 (far right). At pH = 7.0, the solution is blue.
Synthetic indicators have been developed that meet these criteria and cover virtually the entire pH range. Figure (PageIndex{7}) shows the approximate pH range over which some common indicators change color and their change in color. In addition, some indicators (such as thymol blue) are polyprotic acids or bases, which change color twice at widely separated pH values.

It is important to be aware that an indicator does not change color abruptly at a particular pH value; instead, it actually undergoes a pH titration just like any other acid or base. As the concentration of HIn decreases and the concentration of In− increases, the color of the solution slowly changes from the characteristic color of HIn to that of In−. As we will see later, the [In−]/[HIn] ratio changes from 0.1 at a pH one unit below pKin to 10 at a pH one unit above pKin. Thus most indicators change color over a pH range of about two pH units.
We have stated that a good indicator should have a pKin value that is close to the expected pH at the equivalence point. For a strong acid–strong base titration, the choice of the indicator is not especially critical due to the very large change in pH that occurs around the equivalence point. In contrast, using the wrong indicator for a titration of a weak acid or a weak base can result in relatively large errors, as illustrated in Figure (PageIndex{8}). This figure shows plots of pH versus volume of base added for the titration of 50.0 mL of a 0.100 M solution of a strong acid (HCl) and a weak acid (acetic acid) with 0.100 M (NaOH). The pH ranges over which two common indicators (methyl red, (pK_{in} = 5.0), and phenolphthalein, (pK_{in} = 9.5)) change color are also shown. The horizontal bars indicate the pH ranges over which both indicators change color cross the HCl titration curve, where it is almost vertical. Hence both indicators change color when essentially the same volume of (NaOH) has been added (about 50 mL), which corresponds to the equivalence point. In contrast, the titration of acetic acid will give very different results depending on whether methyl red or phenolphthalein is used as the indicator. Although the pH range over which phenolphthalein changes color is slightly greater than the pH at the equivalence point of the strong acid titration, the error will be negligible due to the slope of this portion of the titration curve. Just as with the HCl titration, the phenolphthalein indicator will turn pink when about 50 mL of (NaOH) has been added to the acetic acid solution. In contrast, methyl red begins to change from red to yellow around pH 5, which is near the midpoint of the acetic acid titration, not the equivalence point. Adding only about 25–30 mL of (NaOH) will therefore cause the methyl red indicator to change color, resulting in a huge error.

The graph shows the results obtained using two indicators (methyl red and phenolphthalein) for the titration of 0.100 M solutions of a strong acid (HCl) and a weak acid (acetic acid) with 0.100 M (NaOH). Due to the steepness of the titration curve of a strong acid around the equivalence point, either indicator will rapidly change color at the equivalence point for the titration of the strong acid. In contrast, the pKin for methyl red (5.0) is very close to the (pK_a) of acetic acid (4.76); the midpoint of the color change for methyl red occurs near the midpoint of the titration, rather than at the equivalence point.
In general, for titrations of strong acids with strong bases (and vice versa), any indicator with a pKin between about 4.0 and 10.0 will do. For the titration of a weak acid, however, the pH at the equivalence point is greater than 7.0, so an indicator such as phenolphthalein or thymol blue, with pKin > 7.0, should be used. Conversely, for the titration of a weak base, where the pH at the equivalence point is less than 7.0, an indicator such as methyl red or bromocresol blue, with pKin < 7.0, should be used.
The existence of many different indicators with different colors and pKin values also provides a convenient way to estimate the pH of a solution without using an expensive electronic pH meter and a fragile pH electrode. Paper or plastic strips impregnated with combinations of indicators are used as “pH paper,” which allows you to estimate the pH of a solution by simply dipping a piece of pH paper into it and comparing the resulting color with the standards printed on the container (Figure (PageIndex{9})).

Summary and Takeaway
Plots of acid–base titrations generate titration curves that can be used to calculate the pH, the pOH, the (pK_a), and the (pK_b) of the system. The shape of a titration curve, a plot of pH versus the amount of acid or base added, provides important information about what is occurring in solution during a titration. The shapes of titration curves for weak acids and bases depend dramatically on the identity of the compound. The equivalence point of an acid–base titration is the point at which exactly enough acid or base has been added to react completely with the other component. The equivalence point in the titration of a strong acid or a strong base occurs at pH 7.0. In titrations of weak acids or weak bases, however, the pH at the equivalence point is greater or less than 7.0, respectively. The pH tends to change more slowly before the equivalence point is reached in titrations of weak acids and weak bases than in titrations of strong acids and strong bases. The pH at the midpoint, the point halfway on the titration curve to the equivalence point, is equal to the (pK_a) of the weak acid or the (pK_b) of the weak base. Thus titration methods can be used to determine both the concentration and the (pK_a) (or the (pK_b)) of a weak acid (or a weak base). Acid–base indicators are compounds that change color at a particular pH. They are typically weak acids or bases whose changes in color correspond to deprotonation or protonation of the indicator itself.