La primera ley de la termodinámica rige los cambios en la función de estado que hemos denominado energía interna ( (U )). Los cambios en la energía interna (ΔU) están estrechamente relacionados con los cambios en la entalpía (ΔH), que es una medida del flujo de calor entre un sistema y sus alrededores a presión constante. También aprendiste anteriormente que el cambio de entalpía para una reacción química se puede calcular usando valores tabulados de entalpías de formación. Sin embargo, esta información no nos dice si un proceso o reacción en particular ocurrirá espontáneamente.
Consideremos un ejemplo familiar de cambio espontáneo. Si se permite que una sartén caliente que se acaba de retirar de la estufa entre en contacto con un objeto más frío, como agua fría en un fregadero, el calor fluirá desde el objeto más caliente al más frío, en este caso generalmente liberando vapor . Finalmente, ambos objetos alcanzarán la misma temperatura, a un valor entre las temperaturas iniciales de los dos objetos. Esta transferencia de calor de un objeto caliente a uno más frío obedece a la primera ley de la termodinámica: la energía se conserva.
Ahora considere el mismo proceso a la inversa. Supongamos que una sartén caliente en un fregadero de agua fría se calienta mientras el agua se enfría. Mientras la sartén gane la misma cantidad de energía térmica y el agua la pierda, la primera ley de la termodinámica se cumpliría. Sin embargo, todos sabemos que tal proceso no puede ocurrir: el calor siempre fluye de un objeto caliente a uno frío, nunca en la dirección inversa. Es decir, por sí sola, la magnitud del flujo de calor asociado con un proceso no predice si el proceso ocurrirá espontáneamente.
Durante muchos años, los químicos y físicos intentaron identificar una sola cantidad medible que les permitiera predecir si un proceso o reacción particular ocurriría espontáneamente. Inicialmente, muchos de ellos se centraron en los cambios de entalpía e hipotetizaron que un proceso exotérmico siempre sería espontáneo. Pero aunque es cierto que muchos, si no la mayoría, los procesos espontáneos son exotérmicos, también hay muchos procesos espontáneos que no son exotérmicos. Por ejemplo, a una presión de 1 atm, el hielo se derrite espontáneamente a temperaturas superiores a 0 ° C, sin embargo, este es un proceso endotérmico porque el calor se absorbe. De manera similar, muchas sales (como NH 4 NO 3 , NaCl y KBr) se disuelven espontáneamente en agua a pesar de que absorben el calor del entorno a medida que se disuelven (es decir, ΔH ] solución > 0). Las reacciones también pueden ser tanto espontáneas como altamente endotérmicas, como la reacción del hidróxido de bario con tiocianato de amonio que se muestra en la Figura ( PageIndex {1} ).

Por lo tanto, la entalpía no es el único factor que determina si un proceso es espontáneo. Por ejemplo, después de que un cubo de azúcar se haya disuelto en un vaso de agua para que las moléculas de sacarosa se dispersen uniformemente en una solución diluida, nunca se unen espontáneamente en solución para formar un cubo de azúcar. Además, las moléculas de un gas permanecen distribuidas uniformemente en todo el volumen de un bulbo de vidrio y nunca se ensamblan espontáneamente en solo una porción del volumen disponible. Para ayudar a explicar por qué estos fenómenos proceden espontáneamente en una sola dirección requiere una función de estado adicional llamada entropía (S) , una propiedad termodinámica de todas las sustancias que es proporcional a su grado de “trastorno”. En el Capítulo 13, presentamos el concepto de entropía en relación con la formación de soluciones. Aquí exploramos más a fondo la naturaleza de esta función de estado y la definimos matemáticamente.
Entropía
Los cambios químicos y físicos en un sistema pueden estar acompañados por un aumento o una disminución en el trastorno del sistema, correspondiente a un aumento en la entropía (ΔS> 0) o una disminución en la entropía (ΔS <0), respectivamente . Como con cualquier otra función de estado, el cambio en la entropía se define como la diferencia entre las entropías de los estados final e inicial: ΔS = S f – S i .
Cuando un gas se expande en el vacío, su entropía aumenta porque el volumen aumentado permite un mayor desorden atómico o molecular. Cuanto mayor es el número de átomos o moléculas en el gas, mayor es el desorden. La magnitud de la entropía de un sistema depende del número de estados microscópicos, o microestados, asociados con él (en este caso, el número de átomos o moléculas); es decir, cuanto mayor es el número de microestados, mayor es la entropía.
Podemos ilustrar los conceptos de microestados y entropía usando una baraja de cartas, como se muestra en la Figura ( PageIndex {2} ). En cualquier mazo nuevo, las 52 cartas están organizadas por cuatro palos, con cada palo dispuesto en orden descendente. Sin embargo, si las cartas se barajan, hay aproximadamente 10 68 formas diferentes en que podrían organizarse, lo que corresponde a 10 68 estados microscópicos diferentes. La entropía de un nuevo mazo de cartas ordenado es, por lo tanto, baja, mientras que la entropía de un mazo aleatorio es alta. Los juegos de cartas asignan un valor más alto a una mano que tiene un bajo grado de desorden. En juegos como el póker de cinco cartas, solo 4 de las 2,598,960 manos posibles diferentes, o microestados, contienen la disposición de cartas altamente ordenada y valorada llamada escalera real, casi 1.1 millones de manos contienen un par, y más de 1.3 millones de manos son completamente desordenado y por lo tanto no tiene valor. Debido a que los dos últimos arreglos son mucho más probables que el primero, el valor de una mano de póker es inversamente proporcional a su entropía.

Podemos ver cómo calcular este tipo de probabilidades para un sistema químico considerando las posibles disposiciones de una muestra de cuatro moléculas de gas en un contenedor de dos bombillas (Figura ( PageIndex {3} )). Hay cinco arreglos posibles: las cuatro moléculas en el bulbo izquierdo (I); tres moléculas en la bombilla izquierda y una en la bombilla derecha (II); dos moléculas en cada bulbo (III); una molécula en el bulbo izquierdo y tres moléculas en el bulbo derecho (IV); y cuatro moléculas en el bulbo derecho (V). Si asignamos un color diferente a cada molécula para seguirlo en esta discusión (recuerde, sin embargo, que en realidad las moléculas son indistinguibles entre sí), podemos ver que hay 16 formas diferentes en que las cuatro moléculas pueden distribuirse en los bulbos, cada uno correspondiente a un microestado particular. Como se muestra en la Figura ( PageIndex {3} ), el arreglo I está asociado con un solo microestado, al igual que el arreglo V, por lo que cada arreglo tiene una probabilidad de 1/16. Los arreglos II y IV tienen una probabilidad de 4/16 porque cada uno puede existir en cuatro microestados. De manera similar, pueden ocurrir seis microestados diferentes como disposición III, lo que hace que la probabilidad de esta disposición sea 6/16. Por lo tanto, la disposición que esperaríamos encontrar, con la mitad de las moléculas de gas en cada bulbo, es la disposición más probable. Los otros no son imposibles sino simplemente menos probables.
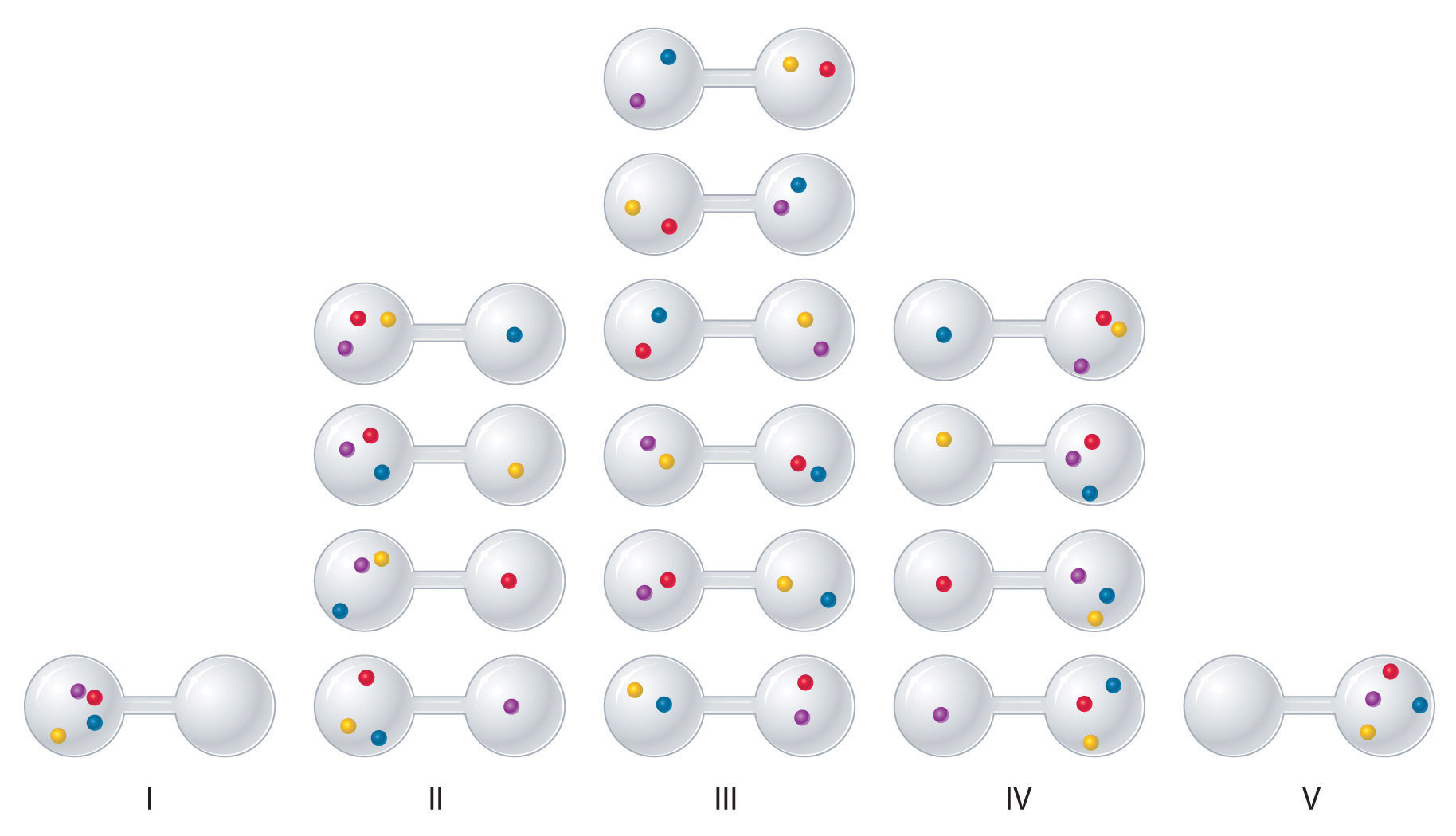
Hay 16 formas diferentes de distribuir cuatro moléculas de gas entre los bulbos, y cada distribución corresponde a un microestado particular. Los arreglos I y V producen cada uno un microestado único con una probabilidad de 1/16. Este arreglo particular es tan improbable que probablemente no se observe. Los arreglos II y IV producen cada uno cuatro microestados, con una probabilidad de 4/16. El arreglo III, con la mitad de las moléculas de gas en cada bulbo, tiene una probabilidad de 6/16. Es el que abarca más microestados, por lo que es el más probable.
En lugar de cuatro moléculas de gas, consideremos ahora 1 L de un gas ideal a temperatura y presión estándar (STP), que contiene 2.69 × 10 22 moléculas (6.022 × 10 23 [ 19459028] moléculas / 22,4 L). Si permitimos que la muestra de gas se expanda en un segundo contenedor de 1 L, la probabilidad de encontrar todas las moléculas de 2.69 × 10 22 en un contenedor y ninguna en el otro en un momento dado es extremadamente pequeña, aproximadamente ( frac {2} {2.69 times 10 ^ {22}} ). La probabilidad de tal ocurrencia es efectivamente cero. Aunque nada impide que las moléculas en la muestra de gas ocupen solo una de las dos bombillas, esa disposición particular es tan improbable que nunca se observa realmente. Sin embargo, la probabilidad de arreglos con un número esencialmente igual de moléculas en cada bulbo es bastante alta, porque hay muchos microestados equivalentes en los que las moléculas se distribuyen por igual. Por lo tanto, una muestra macroscópica de un gas ocupa todo el espacio disponible, simplemente porque esta es la disposición más probable.
Un sistema desordenado tiene un mayor número de microestados posibles que un sistema ordenado, por lo que tiene una entropía más alta. Esto se ve más claramente en los cambios de entropía que acompañan a las transiciones de fase, como sólido a líquido o líquido a gas. Como saben, un sólido cristalino está compuesto por una serie ordenada de moléculas, iones o átomos que ocupan posiciones fijas en una red, mientras que las moléculas en un líquido son libres de moverse y caer dentro del volumen del líquido; Las moléculas en un gas tienen aún más libertad de movimiento que las de un líquido. Cada grado de movimiento aumenta el número de microestados disponibles, lo que resulta en una mayor entropía. Por lo tanto, la entropía de un sistema debe aumentar durante la fusión (ΔS fus > 0). De manera similar, cuando un líquido se convierte en vapor, la mayor libertad de movimiento de las moléculas en la fase gaseosa significa que ΔS vap > 0. Por el contrario, los procesos inversos (condensando un vapor para formar un líquido o congelar un líquido para formar un sólido) debe ir acompañado de una disminución en la entropía del sistema: ΔS <0.
Los experimentos muestran que la magnitud de ΔS vap es 80–90 J / (mol • K) para una amplia variedad de líquidos con diferentes puntos de ebullición. Sin embargo, los líquidos que tienen estructuras altamente ordenadas debido al enlace de hidrógeno u otras interacciones intermoleculares tienden a tener valores significativamente más altos de ΔS vap . Por ejemplo, ΔS vap para agua es 102 J / (mol • K). Otro proceso que se acompaña de cambios de entropía es la formación de una solución. Como se ilustra en la Figura ( PageIndex {4} ), se espera que la formación de una solución líquida a partir de un sólido cristalino (el soluto) y un solvente líquido produzca un aumento en el número de microestados disponibles del sistema y, por lo tanto, su entropía De hecho, la disolución de una sustancia como el NaCl en agua altera tanto la red cristalina ordenada de NaCl como la estructura de agua ordenada con enlaces de hidrógeno, lo que lleva a un aumento de la entropía del sistema. Al mismo tiempo, sin embargo, cada ion disuelto de Na + se hidrata mediante una disposición ordenada de al menos seis moléculas de agua, y los iones Cl – también hacen que el agua adopte un particular estructura local Ambos efectos aumentan el orden del sistema, lo que lleva a una disminución de la entropía. El cambio global de entropía para la formación de una solución, por lo tanto, depende de las magnitudes relativas de estos factores opuestos. En el caso de una solución de NaCl, la interrupción de la estructura cristalina de NaCl y las interacciones unidas por hidrógeno en el agua es cuantitativamente más importante, por lo que ΔS solución > 0.
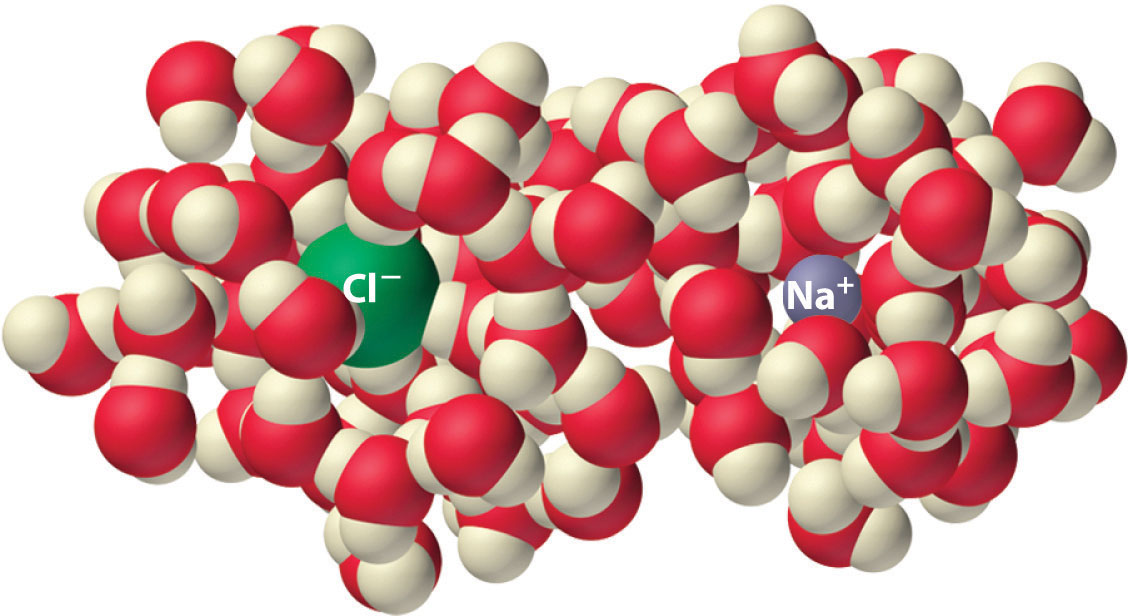
La disolución de NaCl en agua produce un aumento en la entropía del sistema. Sin embargo, cada ion hidratado forma una disposición ordenada con las moléculas de agua, lo que disminuye la entropía del sistema. La magnitud del aumento es mayor que la magnitud de la disminución, por lo que el cambio de entropía general para la formación de una solución de NaCl es positivo.
Cambios reversibles e irreversibles
Los cambios en la entropía (ΔS), junto con los cambios en la entalpía (ΔH), nos permiten predecir en qué dirección ocurrirá espontáneamente un cambio químico o físico. Sin embargo, antes de discutir cómo hacerlo, debemos entender la diferencia entre un proceso reversible y uno irreversible. En un proceso reversible, cada estado intermedio entre los extremos es un estado de equilibrio, independientemente de la dirección del cambio. En contraste, un proceso irreversible es aquel en el que los estados intermedios no son estados de equilibrio, por lo que el cambio ocurre espontáneamente en una sola dirección. Como resultado, un proceso reversible puede cambiar de dirección en cualquier momento, mientras que un proceso irreversible no puede. Cuando un gas se expande reversiblemente contra una presión externa, como un pistón, por ejemplo, la expansión se puede revertir en cualquier momento invirtiendo el movimiento del pistón; Una vez que se comprime el gas, se puede permitir que se expanda nuevamente y el proceso puede continuar indefinidamente. En contraste, la expansión de un gas en el vacío (P ext = 0) es irreversible porque la presión externa es considerablemente menor que la presión interna del gas. No existen estados de equilibrio, y el gas se expande irreversiblemente. Cuando el gas escapa de un orificio microscópico en un globo al vacío, por ejemplo, el proceso es irreversible; La dirección del flujo de aire no puede cambiar.
Debido a que el trabajo realizado durante la expansión de un gas depende de la presión externa opuesta (w = – P ext ΔV), el trabajo realizado en un proceso reversible siempre es igual o mayor que el trabajo realizado en un proceso irreversible correspondiente: w rev ≥ w irrev . Si un proceso es reversible o irreversible, ΔU = q + w. Como U es una función de estado, la magnitud de ΔU no depende de la reversibilidad y es independiente de la ruta tomada. Entonces
[ΔU = q_ {rev} + w_ {rev} = q_ {irrev} + w_ {irrev} label {Eq1} ]
En otras palabras, ΔU para un proceso es el mismo si ese proceso se lleva a cabo de manera reversible o irreversible. Ahora volvemos a nuestra definición anterior de entropía, utilizando la magnitud del flujo de calor para un proceso reversible (q rev ) para definir la entropía cuantitativamente.
La relación entre la energía interna y la entropía
Debido a que la cantidad de calor transferido (q rev ) es directamente proporcional a la temperatura absoluta de un objeto (T) (q rev ∝ T), más caliente es el objeto, cuanto mayor es la cantidad de calor transferido. Además, agregar calor a un sistema aumenta la energía cinética de los átomos y moléculas componentes y, por lo tanto, su desorden (ΔS ∝ q rev ). Combinando estas relaciones para cualquier proceso reversible,
[q _ { textrm {rev}} = T Delta S ; textrm {y} ; Delta S = dfrac {q _ { textrm {rev}}} {T} label {Eq2 } ]
Debido a que el numerador (q rev ) se expresa en unidades de energía (julios), las unidades de ΔS son julios / kelvin (J / K). Reconociendo que el trabajo realizado en un proceso reversible a presión constante es w rev = −PΔV, podemos expresar la ecuación ( ref {Eq1} ) de la siguiente manera:
[ begin {align} ΔU & = q_ {rev} + w_ {rev} \ [4pt] & = TΔS – PΔV label {Eq3} end {align} ]
Así, el cambio en la energía interna del sistema está relacionado con el cambio en la entropía, la temperatura absoluta y el trabajo (PV ) realizado.
Para ilustrar el uso de la ecuación ( ref {Eq2} ) y la ecuación ( ref {Eq3} ), consideramos dos procesos reversibles antes de pasar a un proceso irreversible. Cuando se permite que una muestra de un gas ideal se expanda reversiblemente a temperatura constante, se debe agregar calor al gas durante la expansión para mantener su (T ) constante (Figura ( PageIndex {5} )). La energía interna del gas no cambia porque la temperatura del gas no cambia; es decir, (ΔU = 0 ) y (q_ {rev} = −w_ {rev} ). Durante la expansión, ΔV> 0, por lo que el gas realiza trabajos en su entorno:
[w_ {rev} = −PΔV <0. ]
Según la ecuación ( ref {Eq3} ), esto significa que q rev debe aumentar durante la expansión; es decir, el gas debe absorber el calor de los alrededores durante la expansión, y los alrededores deben ceder esa misma cantidad de calor. Por lo tanto, el cambio de entropía del sistema es ΔS sys = + q rev / T, y el cambio de entropía del entorno es
[ΔS_ {surr} = – dfrac {q_ {rev}} {T}. ]
El cambio correspondiente en la entropía del universo es el siguiente:
[ begin {align *} Delta S _ { textrm {univ}} & = Delta S _ { textrm {sys}} + Delta S _ { textrm {surr}} \ [4pt] & = dfrac {q _ { textrm {rev}}} {T} + left (- dfrac {q_ textrm {rev}} {T} right) \ [4pt] & = 0 label {Eq4} end {align *} ]
Por lo tanto, no se ha producido ningún cambio en ΔS univ .
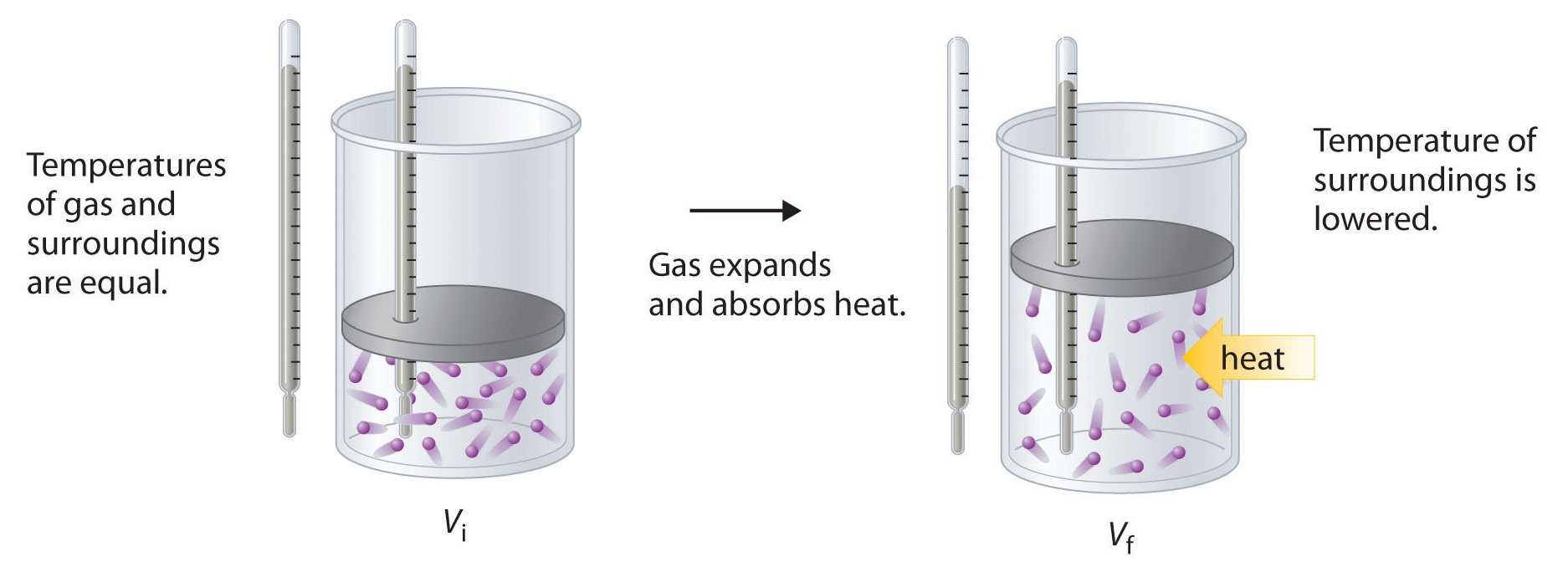
En el estado inicial (arriba), las temperaturas de un gas y el entorno son las mismas. Durante la expansión reversible del gas, se debe agregar calor al gas para mantener una temperatura constante. Por lo tanto, la energía interna del gas no cambia, pero el trabajo se realiza en los alrededores. En el estado final (abajo), la temperatura de los alrededores es más baja porque el gas ha absorbido el calor de los alrededores durante la expansión.
Ahora considere la fusión reversible de una muestra de hielo a 0 ° C y 1 atm. La entalpía de fusión del hielo es 6.01 kJ / mol, lo que significa que 6.01 kJ de calor se absorben reversiblemente de los alrededores cuando 1 mol de hielo se derrite a 0 ° C, como se ilustra en la Figura ( PageIndex {6} ). Los alrededores constituyen una muestra de espuma de carbono de baja densidad que es térmicamente conductora, y el sistema es el cubo de hielo que se le ha colocado. La dirección del flujo de calor a lo largo del gradiente de temperatura resultante se indica con una flecha. De la ecuación ( ref {Eq2} ), vemos que la entropía de fusión del hielo se puede escribir de la siguiente manera:
( Delta S _ { textrm {fus}} = dfrac {q _ { textrm {rev}}} {T} = dfrac { Delta H _ { textrm {fus}}} {T} etiqueta {Eq5} )
Por convención, un termograma muestra regiones frías en azul, regiones cálidas en rojo y regiones térmicamente intermedias en verde. Cuando se coloca un cubo de hielo (el sistema, azul oscuro) en la esquina de una muestra cuadrada de espuma de carbono de baja densidad con conductividad térmica muy alta, la temperatura de la espuma se reduce (pasando de rojo a verde). A medida que el hielo se derrite, aparece un gradiente de temperatura, que va de cálido a muy frío. Una flecha indica la dirección del flujo de calor desde los alrededores (rojo y verde) hasta el cubo de hielo. La cantidad de calor perdido por los alrededores es la misma que la cantidad ganada por el hielo, por lo que la entropía del universo no cambia.

En este caso, ΔS fus = (6.01 kJ / mol) / (273 K) = 22.0 J / (mol • K) = ΔS sys . La cantidad de calor perdido por los alrededores es la misma que la cantidad ganada por el hielo, entonces ΔS surr = q rev / T = – (6.01 kJ / mol) / (273 K) = −22.0 J / (mol • K). Una vez más, vemos que la entropía del universo no cambia:
ΔS univ = ΔS sys + ΔS surr = 22.0 J / (mol • K) – 22.0 J / (mol • K) = 0 [ 19459012]
En estos dos ejemplos de procesos reversibles, la entropía del universo no cambia. Esto es cierto para todos los procesos reversibles y constituye parte de la segunda ley de la termodinámica: la entropía del universo permanece constante en un proceso reversible, mientras que la entropía del universo aumenta en un proceso irreversible (espontáneo).
Como ejemplo de un proceso irreversible, considere los cambios de entropía que acompañan la transferencia espontánea e irreversible de calor de un objeto caliente a uno frío, como ocurre cuando la lava arrojada desde un volcán fluye hacia el agua fría del océano. La sustancia fría, el agua, gana calor (q> 0), por lo que el cambio en la entropía del agua puede escribirse como ΔS frío = q / T frío . Del mismo modo, la sustancia caliente, la lava, pierde calor (q <0), por lo que su cambio de entropía se puede escribir como ΔS caliente = −q / T caliente , donde T [19459013 ] frío y T caliente son las temperaturas de las sustancias fría y caliente, respectivamente. Por lo tanto, el cambio total de entropía del universo que acompaña a este proceso es
[ Delta S _ { textrm {univ}} = Delta S _ { textrm {cold}} + Delta S _ { textrm {hot}} = dfrac {q} {T _ { textrm {cold }}} + left (- dfrac {q} {T _ { textrm {hot}}} right) label {Eq6} ]
Los numeradores en el lado derecho de la ecuación ( ref {Eq6} ) son iguales en magnitud pero opuestos en signo. Si ΔS univ es positivo o negativo depende de las magnitudes relativas de los denominadores. Por definición, T caliente > T frío , entonces −q / T caliente debe ser menor que q / T frío , y ΔS univ debe ser positivo. Como predice la segunda ley de la termodinámica, la entropía del universo aumenta durante este proceso irreversible. Cualquier proceso para el cual ΔS univ es positivo es, por definición, uno espontáneo que ocurrirá tal como está escrito. Por el contrario, cualquier proceso para el cual ΔS univ es negativo no ocurrirá como está escrito, sino que ocurrirá espontáneamente en la dirección inversa. Por lo tanto, vemos que el calor se transfiere espontáneamente de una sustancia caliente, la lava, a una sustancia fría, el agua del océano. De hecho, si la lava está lo suficientemente caliente (por ejemplo, si está fundida), se puede transferir tanto calor que el agua se convierte en vapor (Figura ( PageIndex {7} )).

Resumen
For a given system, the greater the number of microstates, the higher the entropy. During a spontaneous process, the entropy of the universe increases. [Delta S=frac{q_{textrm{rev}}}{T}]
A measure of the disorder of a system is its entropy (S), a state function whose value increases with an increase in the number of available microstates. A reversible process is one for which all intermediate states between extremes are equilibrium states; it can change direction at any time. In contrast, an irreversible process occurs in one direction only. The change in entropy of the system or the surroundings is the quantity of heat transferred divided by the temperature. The second law of thermodynamics states that in a reversible process, the entropy of the universe is constant, whereas in an irreversible process, such as the transfer of heat from a hot object to a cold object, the entropy of the universe increases.