Uno de los objetivos principales de la termodinámica química es establecer criterios para predecir si una reacción o proceso en particular ocurrirá espontáneamente. Hemos desarrollado uno de estos criterios, el cambio en la entropía del universo: si ΔS univ > 0 para un proceso o una reacción, entonces el proceso ocurrirá espontáneamente como está escrito. Por el contrario, si ΔS univ <0, un proceso no puede ocurrir espontáneamente; si ΔS univ = 0, el sistema está en equilibrio. El signo de ΔS univ es un indicador universalmente aplicable e infalible de la espontaneidad de una reacción. Desafortunadamente, el uso de ΔS univ requiere que calculemos ΔS para un sistema y sus alrededores. Esto no es particularmente útil por dos razones: normalmente estamos mucho más interesados en el sistema que en los alrededores, y es difícil hacer mediciones cuantitativas de los alrededores (es decir, el resto del universo). Un criterio de espontaneidad que se base únicamente en las funciones de estado de un sistema sería mucho más conveniente y lo proporciona una nueva función de estado: la energía libre de Gibbs.
Energía libre de Gibbs y la dirección de las reacciones espontáneas
La energía libre de Gibbs ( (G )), a menudo llamada simplemente energía libre, fue nombrada en honor a J. Willard Gibbs (1838–1903), un físico estadounidense que desarrolló el concepto por primera vez. Se define en términos de otras tres funciones de estado con las que ya está familiarizado: entalpía, temperatura y entropía:
[G = H – TS etiqueta {Eq1} ]
Debido a que es una combinación de funciones de estado, (G ) también es una función de estado.
El criterio para predecir la espontaneidad se basa en ( (ΔG )), el cambio en (G ), a temperatura y presión constantes. Aunque en realidad ocurren muy pocas reacciones químicas en condiciones de temperatura y presión constantes, la mayoría de los sistemas pueden volver a la temperatura y presión iniciales sin afectar significativamente el valor de las funciones del estado termodinámico como (G ). A temperatura y presión constantes,
[ΔG = ΔH – TΔS label {Eq2} ]
donde todas las cantidades termodinámicas son las del sistema. Recuerde que a presión constante, (ΔH = q ), si un proceso es reversible o irreversible, y TΔS = q rev . Usando estas expresiones, podemos reducir la ecuación ( ref {Eq2} ) a (ΔG = q – q_ {rev} ). Por lo tanto, ΔG es la diferencia entre el calor liberado durante un proceso (a través de una ruta reversible o irreversible) y el calor liberado para el mismo proceso que ocurre de manera reversible. Bajo la condición especial en la que un proceso ocurre de manera reversible, q = q rev y ΔG = 0. Como veremos pronto, si (ΔG ) es cero, el sistema está en equilibrio, y habrá No hay cambio neto.
¿Qué pasa con los procesos para los cuales ΔG ≠ 0? Para comprender cómo el signo de ΔG para un sistema determina la dirección en la que el cambio es espontáneo, podemos reescribir la relación entre ( Delta S ) y (q_ {rev} ), discutido anteriormente.
[ Delta S = dfrac {q_ {rev}} {T} ]
con la definición de ( Delta H ) en términos de (q_ {rev} )
[q_ {rev} = ΔH ]
para obtener
[ Delta S _ { textrm {surr}} = – dfrac { Delta H _ { textrm {sys}}} {T} label {Eq3} ]
Por lo tanto, el cambio de entropía de los alrededores está relacionado con el cambio de entalpía del sistema. Hemos dicho que para una reacción espontánea, (ΔS_ {univ}> 0 ), sustituyendo así obtenemos
[ begin {align} Delta S _ { textrm {univ}} & = Delta S _ { textrm {sys}} + Delta S _ { textrm {surr}}> 0 \ [4pt] & = Delta S _ { textrm {sys}} – dfrac { Delta H _ { textrm {sys}}} {T}> 0 end {align} ]
Multiplicar ambos lados de la desigualdad por −T invierte el signo de la desigualdad; reorganización,
[ΔH_ {sys} −TΔS_ {sys} <0 ]
que es igual a (ΔG ) (Ecuación ( ref {Eq2} )). Por lo tanto, podemos ver que para un proceso espontáneo, (ΔG <0 ).
La relación entre el cambio de entropía del entorno y el calor ganado o perdido por el sistema proporciona la conexión clave entre las propiedades termodinámicas del sistema y el cambio en la entropía del universo. La relación que se muestra en la Ecuación ( ref {Eq2} ) nos permite predecir la espontaneidad al enfocarnos exclusivamente en las propiedades termodinámicas y la temperatura del sistema. Predecimos que los procesos altamente exotérmicos ( (ΔH ll 0 )) que aumentan el desorden de un sistema ( (ΔS_ {sys} gg 0 )) por lo tanto ocurrirían espontáneamente. Un ejemplo de tal proceso es la descomposición del fertilizante de nitrato de amonio. El nitrato de amonio también se usó para destruir el Edificio Federal Murrah en Oklahoma City, Oklahoma, en 1995. Para un sistema a temperatura y presión constantes, podemos resumir los siguientes resultados:
- Si (ΔG <0 ), el proceso ocurre espontáneamente.
- Si (ΔG = 0 ), el sistema está en equilibrio.
- Si (ΔG> 0 ), el proceso no es espontáneo como está escrito, sino que ocurre espontáneamente en la dirección inversa.
Para comprender mejor cómo los diversos componentes de ΔG determinan si un proceso ocurre espontáneamente, ahora observamos un cambio físico simple y familiar: la conversión de agua líquida en vapor de agua. Si este proceso se lleva a cabo a 1 atm y el punto de ebullición normal de 100.00 ° C (373.15 K), podemos calcular ΔG a partir del valor medido experimentalmente de ΔH vap (40.657 kJ / mol). Para vaporizar 1 mol de agua, (ΔH = 40,657; J ), entonces el proceso es altamente endotérmico. De la definición de ΔS (Ecuación ( ref {Eq3} )), sabemos que para 1 mol de agua,
[ begin {align *} Delta S _ { textrm {vap}} & = dfrac { Delta H _ { textrm {vap}}} {T_ textrm b} \ [4pt] & = dfrac { textrm {40,657 J}} { textrm {373.15 K}} \ [4pt] & = textrm {108.96 J / K} end {align *} ]
Por lo tanto, hay un aumento en el desorden del sistema. En el punto de ebullición normal del agua,
[ begin {align *} Delta G_ {100 ^ circ textrm C} & = Delta H_ {100 ^ circ textrm C} -T Delta S_ {100 ^ circ textrm C } \ [4pt] & = textrm {40,657 J} – [( textrm {373.15 K}) ( textrm {108.96 J / K})] \ [4pt] & = textrm {0 J} end {alinear *} ]
La energía requerida para la vaporización compensa el aumento del desorden del sistema. Así, ΔG = 0, y el líquido y el vapor están en equilibrio, como es el caso de cualquier líquido en su punto de ebullición en condiciones estándar.
Supongamos ahora que sobrecalentamos 1 mol de agua líquida a 110 ° C. El valor de ΔG para la vaporización de 1 mol de agua a 110 ° C, suponiendo que ΔH y ΔS no cambian significativamente con la temperatura, se convierte en
[ begin {align *} Delta G_ {110 ^ circ textrm C} & = Delta HT Delta S \ [4pt] & = textrm {40,657 J} – [( textrm { 383.15 K}) ( textrm {108.96 J / K})] \ [4pt] & = – textrm {1091 J} end {align *} ]
A 110 ° C, (ΔG <0 ), y se predice que la vaporización ocurrirá espontáneamente e irreversiblemente.
También podemos calcular (ΔG ) para la vaporización de 1 mol de agua a una temperatura inferior a su punto de ebullición normal, por ejemplo, 90 ° C, haciendo los mismos supuestos:
[ begin {align *} Delta G_ {90 ^ circ textrm C} & = Delta HT Delta S \ [4pt] & = textrm {40,657 J} – [( textrm { 363.15 K}) ( textrm {108.96 J / K})] \ [4pt] & = textrm {1088 J} end {align *} ]
A 90 ° C, ΔG> 0, y el agua no se convierte espontáneamente en vapor de agua. Cuando usamos todos los dígitos en la pantalla de la calculadora para realizar nuestros cálculos, ΔG 110 ° C = 1090 J = −ΔG 90 ° C , como podríamos predecir.
También podemos calcular la temperatura a la que el agua líquida está en equilibrio con el vapor de agua. Insertar los valores de ΔH y ΔS en la definición de ΔG (Ecuación ( ref {Eq2} )), establecer (ΔG = 0 ) y resolver para (T ),
0 J = 40,657 J − T (108,96 J / K)
T = 373,15 K
Así (ΔG = 0 ) a T = 373,15 K y 1 atm, lo que indica que el agua líquida y el vapor de agua están en equilibrio; Esta temperatura se llama el punto de ebullición normal del agua. A temperaturas superiores a 373,15 K, (ΔG ) es negativo y el agua se evapora de forma espontánea e irreversible. Por debajo de 373.15 K, (ΔG ) es positivo, y el agua no se evapora espontáneamente. En cambio, el vapor de agua a una temperatura inferior a 373,15 K y 1 atm se condensará de forma espontánea e irreversible en agua líquida. La Figura ( PageIndex {1} ) muestra cómo los términos (ΔH ) y (TΔS ) varían con la temperatura para la vaporización del agua. Cuando las dos líneas se cruzan, (ΔG = 0 ) y (ΔH = TΔS ).
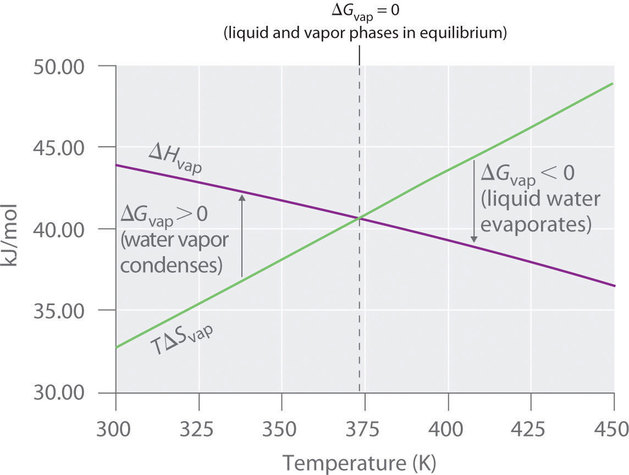
Una situación similar surge en la conversión de clara de huevo líquida a sólida cuando un huevo se hierve. El componente principal de la clara de huevo es una proteína llamada albúmina, que se mantiene en una estructura compacta y ordenada por una gran cantidad de enlaces de hidrógeno. Romperlos requiere un aporte de energía (ΔH> 0), que convierte la albúmina en una estructura altamente desordenada en la que las moléculas se agregan como un sólido desorganizado (ΔS> 0). A temperaturas superiores a 373 K, el término TΔS domina y ΔG <0, por lo que la conversión de un huevo crudo en un huevo duro es un proceso irreversible y espontáneo por encima de 373 K.
La relación entre ΔG y el trabajo
En la subsección anterior, aprendimos que el valor de ΔG nos permite predecir la espontaneidad de un cambio físico o químico. Además, la magnitud de ΔG para un proceso proporciona otra información importante. El cambio en la energía libre (ΔG) es igual a la cantidad máxima de trabajo que un sistema puede realizar en el entorno mientras experimenta un cambio espontáneo (a temperatura y presión constantes): ΔG = w max . Para ver por qué esto es cierto, veamos nuevamente las relaciones entre energía libre, entalpía y entropía expresadas en la Ecuación ( ref {Eq2} ). Podemos reorganizar esta ecuación de la siguiente manera:
[ΔH = ΔG + TΔS label {Eq4} ]
Esta ecuación nos dice que cuando se libera energía durante un proceso exotérmico (ΔH <0), como durante la combustión de un combustible, parte de esa energía se puede usar para hacer trabajo (ΔG <0), mientras que otra es Se utiliza para aumentar la entropía del universo (TΔS> 0). Solo si el proceso ocurre infinitamente lento de una manera perfectamente reversible, la entropía del universo no cambiará. (Para obtener más información sobre entropía y reversibilidad, consulte la sección anterior). Debido a que ningún sistema real es perfectamente reversible, la entropía del universo aumenta durante todos los procesos que producen energía. Como resultado, ningún proceso que use energía almacenada puede ser 100% eficiente; es decir, ΔH nunca será igual a ΔG porque ΔS tiene un valor positivo.
Uno de los principales desafíos que enfrentan los ingenieros es maximizar la eficiencia de convertir la energía almacenada en trabajo útil o convertir una forma de energía en otra. Como se indica en la Tabla ( PageIndex {1} ), las eficiencias de varios dispositivos de conversión de energía varían ampliamente. Por ejemplo, un motor de combustión interna generalmente usa solo del 25% al 30% de la energía almacenada en el combustible de hidrocarburos para realizar el trabajo; El resto de la energía almacenada se libera en forma inutilizable como calor. En contraste, los motores híbridos de gas y electricidad, ahora utilizados en varios modelos de automóviles, ofrecen aproximadamente un 50% más de eficiencia de combustible. Un generador eléctrico grande es altamente eficiente (aproximadamente el 99%) en la conversión de energía mecánica a eléctrica, pero una bombilla incandescente típica es uno de los dispositivos menos eficientes conocidos (solo aproximadamente el 5% de la energía eléctrica se convierte en luz). En contraste, una célula de hígado de mamífero es una máquina relativamente eficiente y puede usar combustibles como la glucosa con una eficiencia del 30% al 50%.
| Dispositivo | Conversión de energía | Eficiencia aproximada (%) |
|---|---|---|
| generador eléctrico grande | mecánico → eléctrico | 99 |
| batería química | químico → eléctrico | 90 |
| horno casero | químico → calor | 65 |
| pequeña herramienta eléctrica | eléctrico → mecánico | 60 |
| motor del transbordador espacial | químico → mecánico | 50 |
| célula de hígado de mamífero | químico → químico | 30–50 |
| célula de hoja de espinaca | luz → químico | 30 |
| motor de combustión interna | químico → mecánico | 25–30 |
| luz fluorescente | eléctrico → luz | 20 |
| célula solar | luz → electricidad | 10-20 |
| bombilla incandescente | electricidad → luz | 5 |
| célula de levadura | químico → químico | 2–4 |
Cambio estándar de energía libre
Hemos visto que no hay forma de medir las entalpías absolutas, aunque podemos medir los cambios en la entalpía (ΔH) durante una reacción química. Debido a que la entalpía es uno de los componentes de la energía libre de Gibbs, en consecuencia no podemos medir las energías libres absolutas; solo podemos medir los cambios en la energía libre. El cambio estándar de energía libre (ΔG °) es el cambio en la energía libre cuando una sustancia o un conjunto de sustancias en sus estados estándar se convierte en una o más sustancias, también en sus estados estándar. El cambio estándar de energía libre se puede calcular a partir de la definición de energía libre, si se conocen los cambios estándar de entalpía y entropía, utilizando la Ecuación ( ref {Eq5} ):
[ΔG ° = ΔH ° – TΔS ° label {Eq5} ]
Si ΔS ° y ΔH ° para una reacción tienen el mismo signo, entonces el signo de ΔG ° depende de las magnitudes relativas de los términos ΔH ° y TΔS °. Es importante reconocer que un valor positivo de ΔG ° para una reacción no significa que no se formarán productos si los reactivos en sus estados estándar se mezclan; solo significa que en equilibrio las concentraciones de los productos serán menores que las concentraciones de los reactivos.
Los valores tabulados de las energías de formación libres estándar permiten a los químicos calcular los valores de ΔG ° para una amplia variedad de reacciones químicas en lugar de tener que medirlas en el laboratorio. La energía libre estándar de formación ( (ΔG ^ ∘_f )) de un compuesto es el cambio en la energía libre que ocurre cuando se forma 1 mol de una sustancia en su estado estándar a partir de los elementos componentes en sus estados estándar. Por definición, la energía libre estándar de formación de un elemento en su estado estándar es cero a 298.15 K. Un mol de gas Cl 2 a 298.15 K, por ejemplo, tiene ( Delta G ^ ∘_f = 0 ). La energía libre estándar de formación de un compuesto se puede calcular a partir de la entalpía estándar de formación (ΔH ∘ f ) y la entropía estándar de formación (ΔS ∘ f ) utilizando la definición de energía libre:
[ Delta G ^ o_ {f} = ΔH ^ o_ {f} −TΔS ^ o_ {f} label {Eq6} ]
El uso de energías de formación libres estándar para calcular la energía libre estándar de una reacción es análogo al cálculo de los cambios de entalpía estándar de las entalpías de formación estándar usando la regla familiar de “productos menos reactivos”:
[ΔG ^ o_ {rxn} = sum mΔG ^ o_ {f} (productos) – sum nΔ ^ o_ {f} (reactivos) label {Eq7a} ]
donde myn son los coeficientes estequiométricos de cada producto y reactivo en la ecuación química equilibrada. Un ΔG ° negativo muy grande indica una fuerte tendencia a que los productos se formen espontáneamente a partir de reactivos; sin embargo, no necesariamente indica que la reacción ocurrirá rápidamente. Para hacer esta determinación, necesitamos evaluar la cinética de la reacción.
Los valores calculados de ΔG ° son extremadamente útiles para predecir si una reacción ocurrirá espontáneamente si los reactivos y los productos se mezclan en condiciones estándar. Sin embargo, debemos tener en cuenta que muy pocas reacciones se llevan a cabo realmente en condiciones estándar, y los valores calculados de ΔG ° pueden no decirnos si una reacción dada ocurrirá espontáneamente en condiciones no estándar. Lo que determina si una reacción ocurrirá espontáneamente es el cambio de energía libre (ΔG) bajo las condiciones experimentales reales, que generalmente son diferentes de ΔG °. Si los términos ΔH y TΔS para una reacción tienen el mismo signo, por ejemplo, entonces es posible revertir el signo de ΔG cambiando la temperatura, convirtiendo así una reacción que no es termodinámicamente espontánea, teniendo K eq [ 19459011] <1, a uno que tenga K eq > 1, o viceversa. Debido a que ΔH y ΔS generalmente no varían mucho con la temperatura en ausencia de un cambio de fase, podemos usar valores tabulados de ΔH ° y ΔS ° para calcular ΔG ° a varias temperaturas, siempre que no ocurra un cambio de fase en el rango de temperatura considerado.
The effect of temperature on the spontaneity of a reaction, which is an important factor in the design of an experiment or an industrial process, depends on the sign and magnitude of both ΔH° and ΔS°. The temperature at which a given reaction is at equilibrium can be calculated by setting ΔG° = 0 in Equation (ref{Eq5}), as illustrated in Example (PageIndex{4}).
Summary
- The change in Gibbs free energy, which is based solely on changes in state functions, is the criterion for predicting the spontaneity of a reaction.
- Free-energy change:
[ΔG = ΔH − TΔS onumber]
- Standard free-energy change:
[ΔG° = ΔH° − TΔS° onumber]
We can predict whether a reaction will occur spontaneously by combining the entropy, enthalpy, and temperature of a system in a new state function called Gibbs free energy (G). The change in free energy (ΔG) is the difference between the heat released during a process and the heat released for the same process occurring in a reversible manner. If a system is at equilibrium, ΔG = 0. If the process is spontaneous, ΔG < 0. If the process is not spontaneous as written but is spontaneous in the reverse direction, ΔG > 0. At constant temperature and pressure, ΔG is equal to the maximum amount of work a system can perform on its surroundings while undergoing a spontaneous change. The standard free-energy change (ΔG°) is the change in free energy when one substance or a set of substances in their standard states is converted to one or more other substances, also in their standard states. The standard free energy of formation (ΔG ∘ f ), is the change in free energy that occurs when 1 mol of a substance in its standard state is formed from the component elements in their standard states. Tabulated values of standard free energies of formation are used to calculate ΔG° for a reaction.