20.6: Potencial celular en condiciones no estándar

El efecto de la concentración en el potencial celular: la ecuación de Nernst

 

Recuerde que el cambio real de energía libre para una reacción en condiciones no estándar, ( Delta {G} ), se da de la siguiente manera:

 

[ Delta {G} = Delta {G °} + RT ln Q label {Eq1} ]

 

También sabemos que (ΔG = −nFE_ {cell} ) (bajo conficiones no estándar) y (ΔG ^ o = −nFE ^ o_ {cell} ) (bajo condiciones estándar). Sustituyendo estas expresiones en la ecuación ( ref {Eq1} ), obtenemos

 

[- nFE_ {cell} = −nFE ^ o_ {cell} + RT ln Q label {Eq2} ]

 

Dividiendo ambos lados de esta ecuación por (- nF ),

 

[E_ textrm {cell} = E ^ circ_ textrm {cell} – left ( dfrac {RT} {nF} right) ln Q label {Eq3} ]

 

La ecuación ( ref {Eq3} ) se llama ecuación de Nernst , en honor al físico y químico alemán Walter Nernst (1864–1941), quien la derivó por primera vez. La ecuación de Nernst es posiblemente la relación más importante en electroquímica. Cuando una reacción redox está en equilibrio ( (ΔG = 0 )), la ecuación ( ref {Eq3} ) se reduce a la ecuación ( ref {Eq31} ) y ( ref {Eq32} ) porque (Q = K ), y no hay transferencia neta de electrones (es decir, E _celda = 0).

 

[E_ textrm {cell} = E ^ circ_ textrm {cell} – left ( dfrac {RT} {nF} right) ln K = 0 label {Eq31} ] [19459014 ]

 

desde

 

[E ^ circ_ textrm {cell} = left ( dfrac {RT} {nF} right) ln K label {Eq32} ]

 

Sustituyendo los valores de las constantes en la ecuación ( ref {Eq3} ) con (T = 298 , K ) y convirtiendo a logaritmos en base 10 da la relación del potencial celular real (E _celda ), el potencial celular estándar (E ° _celda ), y las concentraciones de reactivo y producto a temperatura ambiente (contenido en (Q )):

 

[E _ { textrm {cell}} = E ^ circ_ textrm {cell} – left ( dfrac { textrm {0.0591 V}} {n} right) log Q label {Eq4 } ]

 

 

La ecuación ( ref {Eq4} ) nos permite calcular el potencial asociado con cualquier celda electroquímica a 298 K para cualquier combinación de reactivo y concentraciones de producto bajo cualquier condición. Por lo tanto, podemos determinar la dirección espontánea de cualquier reacción redox en cualquier condición, siempre que tengamos valores tabulados para los potenciales de electrodo estándar relevantes. Observe en la ecuación ( ref {Eq4} ) que el potencial de la celda cambia en 0.0591 / n V por cada cambio de 10 veces en el valor de (Q ) porque log 10 = 1.

 

Ejemplo ( PageIndex {1} )

 

La siguiente reacción procede espontáneamente en condiciones estándar porque la célula E ° > 0 (lo que significa que ΔG ° <0):

 

[ ce {2Ce ^ {4 +} (aq) + 2Cl ^ {-} (aq) -> 2Ce ^ {3 +} (aq) + Cl2 (g)} ; ; E ^ ° _ {cell} = 0.25 , V nonumber ]

 

Calcule (E_ {celda} ) para esta reacción en las siguientes condiciones no estándar y determine si ocurrirá espontáneamente: [Ce ^{4 +} ] = 0.013 M, [ Ce ^{3 +} ] = 0.60 M, [Cl ^– ] = 0.0030 M, (P_ mathrm {Cl_2} ) = 1.0 atm, y T = 25 ° C.

 

Dado: reacción redox equilibrada, potencial celular estándar y condiciones no estándar

 

Preguntado por: potencial celular

 

Estrategia:

 

Determine la cantidad de electrones transferidos durante el proceso redox. Luego use la ecuación de Nernst para encontrar el potencial celular en condiciones no estándar.

 

SOLUCIÓN

 

Podemos usar la información dada y la ecuación de Nernst para calcular la celda E . Además, debido a que la temperatura es de 25 ° C (298 K), podemos usar la ecuación ( ref {Eq4} ) en lugar de la ecuación ( ref {Eq3} ). La reacción general implica la transferencia neta de dos electrones:

 

[2Ce ^ {4 +} _ {(aq)} + 2e ^ – rightarrow 2Ce ^ {3 +} _ {(aq)} nonumber ]

 

[2Cl ^ −_ {(aq)} rightarrow Cl_ {2 (g)} + 2e ^ – nonumber ]

 

entonces n = 2. Sustituyendo las concentraciones dadas en el problema, la presión parcial de Cl ₂ , y el valor de E ° _celda en la ecuación ( ref {Eq4 } ),

 

[ begin {align *} E_ textrm {cell} & = E ^ circ_ textrm {cell} – left ( dfrac { textrm {0.0591 V}} {n} right) log Q \
& = textrm {0.25 V} – left ( dfrac { textrm {0.0591 V}} {2} right) log left ( dfrac {[ mathrm {Ce ^ {3 +}}] ^ 2P_ mathrm {Cl_2}} {[ mathrm {Ce ^ {4 +}}] ^ 2 [ mathrm {Cl ^ -}] ^ 2} right) \
& = textrm {0.25 V} – [( textrm {0.0296 V}) (8.37)] = textrm {0.00 V} end {align *} ]

 

Por lo tanto, la reacción no ocurrirá espontáneamente en estas condiciones (porque E = 0 V y ΔG = 0). La composición especificada es la de una mezcla de equilibrio

 

 

Ejercicio ( PageIndex {1} )

 

El oxígeno molecular no oxidará (MnO_2 ) para permanganato a través de la reacción

 

[ ce {4MnO2 (s) + 3O2 (g) + 4OH ^ {-} (aq) -> 4MnO ^ {-} 4 (aq) + 2H2O (l)} ; ; ; E ° _ {celda} = −0.20 ; V nonumber ]

 

Calcule (E_ {celda} ) para la reacción en las siguientes condiciones no estándar y decida si la reacción ocurrirá espontáneamente: pH 10, (P_ mathrm {O_2} ) = 0.20 atm, [MNO [19459021 ] 4 ^– ] = 1.0 × 10 ⁻⁴ M, y T = 25 ° C.

 

     

Respuesta

     

     

E _celda = −0,22 V; La reacción no ocurrirá espontáneamente.

     

 

 

 

 

El cociente de reacción es por lo tanto (Q = [Zn ^ {2 +}] / [Cu ^ {2 +}] ). Suponga que la celda contiene inicialmente 1.0 M Cu ^{2 +} y 1.0 × 10 ⁻⁶ M Zn ^{2 + [19459030 ] El voltaje inicial medido cuando la celda está conectada puede calcularse a partir de la ecuación ( ref {Eq4} ):}

 

[ begin {align} E_ textrm {cell} & = E ^ circ_ textrm {cell} – left ( dfrac { textrm {0.0591 V}} {n} right) log dfrac {[ mathrm {Zn ^ {2 +}}]} {[ mathrm {Cu ^ {2 +}}]} \
& = textrm {1.10 V} – left ( dfrac { textrm {0.0591 V}} {2} right) log left ( dfrac {1.0 times10 ^ {- 6}} {1.0} right) = textrm {1.28 V} end {align} label { Eq6} ]

 

Por lo tanto, el voltaje inicial es mayor que E ° porque (Q <1 ). A medida que avanza la reacción, [Zn ^{2 +} ] en el compartimento del ánodo aumenta a medida que el electrodo de zinc se disuelve, mientras que [Cu ^{2 +} ] en el compartimiento del cátodo disminuye a medida que se deposita cobre metálico sobre el electrodo. Durante este proceso, la relación Q = [Zn ^{2 +} ] / [Cu ^{2 +} ] aumenta constantemente, y el voltaje de la celda aumenta constantemente. por lo tanto disminuye constantemente. Eventualmente, [Zn ^{2 +} ] = [Cu ^{2 +} ], entonces Q = 1 y E _{celda [19459022 ] = E ° celda . Más allá de este punto, [Zn ^{2 +} ] continuará aumentando en el compartimiento del ánodo, y [Cu ^{2 +} ] continuará para disminuir en el compartimiento del cátodo. Por lo tanto, el valor de Q aumentará aún más, lo que conducirá a una disminución adicional en la celda E . Cuando las concentraciones en los dos compartimentos son opuestas a las concentraciones iniciales (es decir, 1.0 M Zn ^{2 +} y 1.0 × 10 ⁻⁶ M Cu [19459029 ] 2 ⁺ ), Q = 1.0 × 10 ⁶ , y el potencial celular se reducirá a 0.92 V.}

 

  

 

La variación de la celda E con ( log {Q} ) sobre este rango es lineal con una pendiente de −0.0591 / n, como se ilustra en la Figura ( PageIndex {1} ) A medida que la reacción continúa aún más, (Q ) continúa aumentando, y la celda E continúa disminuyendo. Si ninguno de los electrodos se disuelve por completo, rompiendo así el circuito eléctrico, el voltaje de la celda finalmente llegará a cero. Esta es la situación que ocurre cuando una batería está “agotada”. El valor de (Q ) cuando la celda E = 0 se calcula de la siguiente manera:

 

[ begin {align} E_ textrm {cell} & = E ^ circ_ textrm {cell} – left ( dfrac { textrm {0.0591 V}} {n} right) log Q = 0 \
E ^ circ & = left ( dfrac { textrm {0.0591 V}} {n} right) log Q \
log Q & = dfrac {E ^ circ n} { textrm {0.0591 V}} = dfrac {( textrm {1.10 V}) (2)} { textrm {0.0591 V}} = 37.23 \
Q & = 10 ^ {37.23 } = 1.7 times10 ^ {37} end {align} label {Eq7} ]

 

Recordemos que en equilibrio, (Q = K ). Por lo tanto, la constante de equilibrio para la reacción del metal Zn con Cu ^{2 +} para dar Cu metal y Zn ^{2 +} es 1.7 × 10 ³⁷ a 25 ° C.

 

Células de concentración

 

También se puede generar un voltaje construyendo una celda electroquímica en la que cada compartimento contiene la misma solución activa redox pero a diferentes concentraciones. El voltaje se produce a medida que las concentraciones se equilibran. Supongamos, por ejemplo, que tenemos una celda con 0.010 M AgNO ₃ en un compartimento y 1.0 M AgNO ₃ en el otro. El diagrama celular y las semirreacciones correspondientes son las siguientes:

 

[ ce {Ag (s) , | , Ag ^ {+}} (aq, 0.010 ; M) , || , ce {Ag ^ {+}} (aq, 1.0 ; M) , | , ce {Ag (s)} label {Eq8} ]

 

cátodo:

 

[ ce {Ag ^ {+}} (aq, 1.0 ; M) + ce {e ^ {-}} rightarrow ce {Ag (s)} label {Eq9} ] [ 19459014]

 

ánodo:

 

[ ce {Ag (s)} rightarrow ce {Ag ^ {+}} (aq, 0.010 ; M) + ce {e ^ {-}} label {Eq10} ] [ 19459014]

 

En general

 

[ ce {Ag ^ {+}} (aq, 1.0 ; M) rightarrow ce {Ag ^ {+}} (aq, 0.010 ; M) label {Eq11} ] [19459014 ]

 

A medida que avanza la reacción, la concentración de (Ag ^ + ) aumentará en el compartimento izquierdo (oxidación) a medida que se disuelve el electrodo de plata, mientras que la concentración (Ag ^ + ) en el compartimento derecho (reducción) disminuye a medida que el electrodo en ese compartimento gana masa. Sin embargo, la masa total de (Ag (s) ) en la celda permanecerá constante. Podemos calcular el potencial de la celda usando la ecuación de Nernst, insertando 0 para la celda E ° porque E ° _cátodo = −E ° _ánodo :

 

[ begin {align *} E_ textrm {cell} & = E ^ circ_ textrm {cell} – left ( dfrac { textrm {0.0591 V}} {n} right) log Q \ [4pt] & = 0- left ( dfrac { textrm {0.0591 V}} {1} right) log left ( dfrac {0.010} {1.0} right) \ [4pt] & = textrm {0.12 V} end {align *} ]

 

Una celda electroquímica de este tipo, en la cual los compartimentos anódico y catódico son idénticos, excepto por la concentración de un reactivo, se llama celda de concentración . A medida que avanza la reacción, la diferencia entre las concentraciones de Ag ⁺ en los dos compartimentos disminuirá, al igual que la célula E . Finalmente, cuando la concentración de Ag ⁺ es la misma en ambos compartimentos, se habrá alcanzado el equilibrio y la diferencia de potencial medida entre los dos compartimentos será cero (E _celda = 0 )

 

Ejemplo ( PageIndex {2} )

 

Calcule el voltaje en una celda galvánica que contiene un electrodo de manganeso sumergido en una solución de MnCl 2.0 M ₂ como el cátodo, y un electrodo de manganeso sumergido en un 5.2 × 10 ^{−2 [ 19459030] Solución M de MnSO ₄ como el ánodo (T = 25 ° C).}

 

Dado: celda galvánica, identidades de los electrodos y concentraciones de la solución

 

Preguntado por: voltaje

 

Estrategia:

 

     
1. Escribe la reacción general que ocurre en la celda.

     

2. Determine la cantidad de electrones transferidos. Sustituya este valor en la ecuación de Nernst para calcular el voltaje.

 

 

Solución:

 

A Esta es una celda de concentración, en la cual los compartimientos de electrodos contienen la misma sustancia activa redox pero a diferentes concentraciones. Los aniones (Cl ^– y SO ₄ ²⁻ ) no participan en la reacción, por lo que su identidad no es importante. La reacción general es la siguiente:

 

[ ce {Mn ^ {2 +}} (aq, 2.0 , M) rightarrow ce {Mn ^ {2+}} (aq, 5.2 times 10 ^ {- 2} , M ) nonumber ]

 

B Para la reducción de Mn ^{2 +} (aq) a Mn (s), n = 2. Sustituimos este valor y el Mn dado ^{2 +} concentraciones en la ecuación ( ref {Eq4} ):

 

[ begin {align *} E_ textrm {cell} & = E ^ circ_ textrm {cell} – left ( dfrac { textrm {0.0591 V}} {n} right) log Q \ [4pt] & = textrm {0 V} – left ( dfrac { textrm {0.0591 V}} {2} right) log left ( dfrac {5.2 times10 ^ {- 2} } {2.0} right) \ [4pt] & = textrm {0.047 V} end {align *} ]

 

Así, el manganeso se disolverá del electrodo en el compartimento que contiene la solución más diluida y se depositará en el electrodo en el compartimento que contiene la solución más concentrada.

 

 

Ejercicio ( PageIndex {2} )

 

Supongamos que construimos una celda galvánica colocando dos electrodos de platino idénticos en dos vasos de precipitados que están conectados por un puente de sal. Un vaso de precipitados contiene HCl 1,0 M y el otro una solución de Na 0,010 M ₂ SO ₄ a pH 7,00. Ambas células están en contacto con la atmósfera, con (P_ mathrm {O_2} ) = 0.20 atm. Si la reacción electroquímica relevante en ambos compartimientos es la reducción de cuatro electrones de oxígeno a agua:

 

[ ce {O2 (g) + 4H ^ {+} (aq) + 4e ^ {-} rightarrow 2H2O (l)} nonumber ]

 

¿Cuál será el potencial cuando el circuito esté cerrado?

 

     

Respuesta

     

     

0,41 V

     

 

 

 

Uso de potenciales celulares para medir productos de solubilidad

 

Debido a que los voltajes son relativamente fáciles de medir con precisión utilizando un voltímetro, los métodos electroquímicos proporcionan una forma conveniente de determinar las concentraciones de soluciones muy diluidas y los productos de solubilidad ( (K_ {sp} )) de sustancias escasamente solubles. Como aprendió anteriormente, los productos de solubilidad pueden ser muy pequeños, con valores inferiores o iguales a 10 ⁻³⁰ . Las constantes de equilibrio de esta magnitud son prácticamente imposibles de medir con precisión por métodos directos, por lo que debemos utilizar métodos alternativos que sean más sensibles, como los métodos electroquímicos.

 

  

 

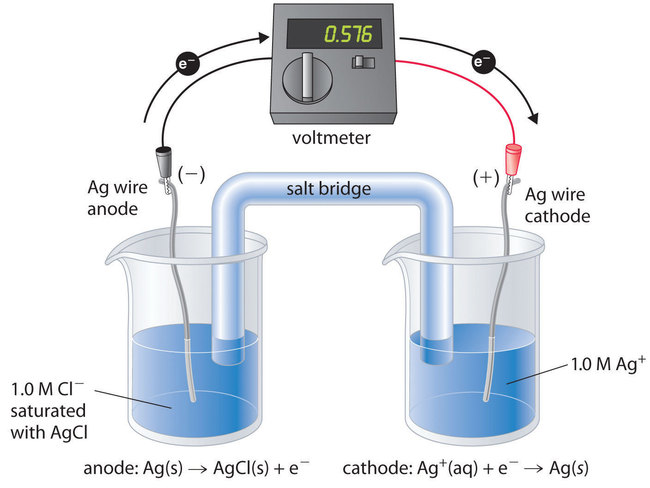
Para comprender cómo se usa una celda electroquímica para medir un producto de solubilidad, considere la celda que se muestra en la Figura ( PageIndex {1} ), que está diseñada para medir el producto de solubilidad del cloruro de plata:

 

[K_ {sp} = [ ce {Ag ^ {+}}] [ ce {Cl ^ {-}}]. nonumber ]

 

En un compartimento, la celda contiene un alambre de plata insertado en una solución de Ag 1,0 M ⁺ ; el otro compartimento contiene un alambre de plata insertado en una solución de Cl [1.0454529] – saturada con AgCl. En este sistema, la concentración de iones Ag ⁺ en el primer compartimento es igual a K _sp . Podemos ver esto dividiendo ambos lados de la ecuación para K _sp por [Cl ^– ] y sustituyendo:

 

[ begin {align *} [ ce {Ag ^ {+}}] & = dfrac {K_ {sp}} {[ ce {Cl ^ {-}}]} \ [4pt] & = Dfrac {K_ {sp}} {1.0} = K_ {sp}. end {align *} ]

 

La reacción celular global es la siguiente:

 

Ag ⁺ (acuoso, concentrado) → Ag ⁺ (acuoso, diluido)

 

Por lo tanto, el voltaje de la celda de concentración debido a la diferencia en [Ag ⁺ ] entre las dos celdas es el siguiente:

 

[ begin {align} E_ textrm {cell} & = textrm {0 V} – left ( dfrac { textrm {0.0591 V}} {1} right) log left ( dfrac {[ mathrm {Ag ^ +}] _ textrm {dilute}} {[ mathrm {Ag ^ +}] _ textrm {concentrado}} right) nonumber \ [4pt] & = – textrm {0.0591 V} log left ( dfrac {K _ { textrm {sp}}} {1.0} right) nonumber \ [4pt] & = – textrm {0.0591 V} log K _ { textrm { sp}} label {Eq122} end {align} ]

 

Al cerrar el circuito, podemos medir el potencial causado por la diferencia en [Ag +] en las dos celdas. En este caso, el voltaje medido experimentalmente de la celda de concentración a 25 ° C es 0.580 V. Resolver la ecuación ( ref {Eq122} ) para (K_ {sp} ),

 

[ begin {align *} log K_ textrm {sp} & = dfrac {-E_ textrm {cell}} { textrm {0.0591 V}} = dfrac {- textrm {0.580 V }} { textrm {0.0591 V}} = – 9.81 \ [4pt]
K_ textrm {sp} & = 1.5 times10 ^ {- 10} end {align *} ]

 

Por lo tanto, una sola medición de potencial puede proporcionar la información que necesitamos para determinar el valor del producto de solubilidad de una sal escasamente soluble.

 

Ejemplo ( PageIndex {3} ): Solubilidad del sulfato de plomo (II)

 

Para medir el producto de solubilidad del sulfato de plomo (II) (PbSO ₄ ) a 25 ° C, construye una celda galvánica como la que se muestra en la Figura ( PageIndex {1} ), que contiene una solución de 1.0 M de un Pb muy soluble ^{2 +} sal [trihidrato de acetato de plomo (II)] en un compartimento que está conectado por un puente de sal a una solución de 1.0 M de Na ₂ SO ₄ saturado con PbSO ₄ en el otro. Luego inserta un electrodo de Pb en cada compartimento y cierra el circuito. Su voltímetro muestra un voltaje de 230 mV. ¿Qué es K _sp para PbSO ₄ ? Informe su respuesta a dos cifras significativas.

 

Dado: celda galvánica, concentraciones de solución, electrodos y voltaje

 

Preguntado por: K _sp

 

Estrategia:

 

     
1. De la información dada, escriba la ecuación para K _sp . Exprese esta ecuación en términos de la concentración de Pb ^{2 +} .

     

2. Determine el número de electrones transferidos en la reacción electroquímica. Sustituya los valores apropiados en la ecuación ( ref {Eq1} ) 2 y resuelva para K _sp .

 

 

Solución:

 

A Has construido una celda de concentración, con un compartimento que contiene una solución 1,0 M de ( ce {Pb ^ {2 +}} ) y el otro que contiene una solución diluida de Pb [ 19459029] 2 ⁺ en 1,0 M Na ₂ SO ₄ . Como para cualquier celda de concentración, el voltaje entre los dos compartimentos se puede calcular usando la ecuación de Nernst. El primer paso es relacionar la concentración de Pb ^{2 +} en la solución diluida con K _sp :

 

[ begin {align *} [ mathrm {Pb ^ {2 +}}] [ mathrm {SO_4 ^ {2-}}] & = K_ textrm {sp} \
[ mathrm {Pb ^ {2+}}] & = dfrac {K_ textrm {sp}} {[ mathrm {SO_4 ^ {2 -}}]} = dfrac {K_ textrm {sp}} { textrm {1.0 M}} = K_ textrm {sp} end {align *} ]

 

B La reducción de Pb ^{2 +} a Pb es un proceso de dos electrones y procede de acuerdo con la siguiente reacción:

 

Pb ^{2 +} (aq, concentrado) → Pb ^{2 +} (aq, diluido)

 

entonces

 

[ begin {align *} E_ textrm {cell} & = E ^ circ_ textrm {cell} – left ( dfrac {0.0591} {n} right) log Q \ [19459031 ] textrm {0.230 V} & = textrm {0 V} – left ( dfrac { textrm {0.0591 V}} {2} right) log left ( dfrac {[ mathrm {Pb ^ { 2 +}}] _ textrm {diluir}} {[ mathrm {Pb ^ {2 +}}] _ textrm {concentrado}} right) = – textrm {0.0296 V} log left ( dfrac {K_ textrm {sp}} {1.0} right) \
-7.77 & = log K_ textrm {sp} \
1.7 times10 ^ {- 8} & = K_ textrm { sp} end {align *} ]

 

 

Ejercicio ( PageIndex {3} )

 

Una célula de concentración similar a la descrita en el Ejemplo ( PageIndex {3} ) contiene una solución 1,0 M de nitrato de lantano [La (NO ₃ ) ₃ ] en un compartimento y una solución 1,0 M de fluoruro de sodio saturado con LaF ₃ en el otro. Se inserta una tira La metálica en cada compartimento y se cierra el circuito. El potencial medido es 0.32 V. ¿Cuál es la K _sp para LaF ₃ ? Informe su respuesta a dos cifras significativas.

 

     

Respuesta

     

     

5,7 × 10 ⁻¹⁷

     

 

 

 

Uso de potenciales celulares para medir concentraciones

 

Otro uso para la ecuación de Nernst es calcular la concentración de una especie dado un potencial medido y las concentraciones de todas las otras especies. Vimos un ejemplo de esto en el Ejemplo ( PageIndex {3} ), en el que las condiciones experimentales se definieron de tal manera que la concentración del ion metálico era igual a K _sp . Las mediciones potenciales también se pueden utilizar para obtener las concentraciones de especies disueltas en otras condiciones, lo que explica el uso generalizado de las células electroquímicas en muchos dispositivos analíticos. Quizás la aplicación más común es la determinación de [H ⁺ ] usando un medidor de pH, como se ilustra a continuación.

 

Ejemplo ( PageIndex {4} ): Medición de pH

 

Suponga que una celda galvánica está construida con un Zn / Zn estándar ^{2 +} pareja en un compartimento y un electrodo de hidrógeno modificado en el segundo compartimento. La presión del gas hidrógeno es de 1.0 atm, pero [H ⁺ ] en el segundo compartimiento es desconocida. El diagrama celular es el siguiente:

 

[ ce {Zn (s)} | ce {Zn ^ {2 +}} (aq, 1.0 , M) || ce {H ^ {+}} (aq,? , M) | ce {H2} (g, 1.0 , atm) | Pt (s) nonumber ]

 

¿Cuál es el pH de la solución en el segundo compartimento si el potencial medido en la celda es de 0.26 V a 25 ° C?

 

Dado: celda galvánica, diagrama celular y potencial celular

 

Preguntado por: pH de la solución

 

Estrategia:

 

     
1. Escribe la reacción celular general.

     

2. Sustituya los valores apropiados en la ecuación de Nernst y resuelva −log [H ⁺ ] para obtener el pH.

 

 

Solución:

 

A En condiciones estándar, la reacción general que ocurre es la reducción de protones por zinc para dar H ₂ (tenga en cuenta que Zn se encuentra debajo de H ₂ en Tabla P2 ):

 

Zn (s) + 2H ^{2 +} (aq) → Zn ^{2 +} (aq) + H ₂ (g) E ° = 0,76 V

 

B Al sustituir los valores dados en la ecuación simplificada de Nernst (Ecuación ( ref {Eq4} )), podemos calcular [H ⁺ ] en condiciones no estándar:

 

[ begin {align *} E_ textrm {cell} & = E ^ circ_ textrm {cell} – left ( dfrac { textrm {0.0591 V}} n right) log left ( dfrac {[ mathrm {Zn ^ {2 +}}] P_ mathrm {H_2}} {[ mathrm {H ^ +}] ^ 2} right) \
textrm {0.26 V} & = textrm {0.76 V} – left ( dfrac { textrm {0.0591 V}} 2 right) log left ( dfrac {(1.0) (1.0)} {[ mathrm {H ^ +} ] ^ 2} right) \
16.9 & = log left ( dfrac {1} {[ mathrm {H ^ +}] ^ 2} right) = log [ mathrm {H ^ +}] ^ {- 2} = (- 2) log [ mathrm {H ^ +}] \
8.46 & = – log [ mathrm {H ^ +}] \
8.5 & = mathrm {pH} end {align *} ]

 

Por lo tanto, el potencial de una celda galvánica se puede utilizar para medir el pH de una solución.

 

 

Ejercicio ( PageIndex {4} )

 

Suponga que trabaja para un laboratorio ambiental y desea utilizar un método electroquímico para medir la concentración de Pb ^{2 +} en aguas subterráneas. Usted construye una celda galvánica usando un electrodo de oxígeno estándar en un compartimento (E ° _cátodo = 1.23 V). El otro compartimento contiene una tira de plomo en una muestra de agua subterránea a la que ha agregado suficiente ácido acético, un ácido orgánico débil, para garantizar la conductividad eléctrica. El diagrama celular es el siguiente:

 

[Pb _ {(s)} ∣Pb ^ {2 +} (aq,? M) ∥H ^ + (aq), 1.0 M∣O_2 (g, 1.0 atm) ∣Pt _ {(s)} no número ]

 

Cuando el circuito está cerrado, la celda tiene un potencial medido de 1.62 V. Utilice Tabla P2 para determinar la concentración de Pb ^{2 +} en el agua subterránea

 

     

Respuesta

     

     

(1.2 veces 10 ^ {- 9} ; M )

     

 

 

 

Resumen

 

La ecuación de Nernst se puede usar para determinar la dirección de la reacción espontánea para cualquier reacción redox en solución acuosa. La ecuación de Nernst nos permite determinar la dirección espontánea de cualquier reacción redox en cualquier condición de reacción a partir de los valores de los potenciales de electrodo estándar relevantes. Las células de concentración consisten en compartimientos anódicos y catódicos que son idénticos, excepto por las concentraciones del reactivo. Debido a que ΔG = 0 en equilibrio, el potencial medido de una celda de concentración es cero en equilibrio (las concentraciones son iguales). Una celda galvánica también puede usarse para medir el producto de solubilidad de una sustancia escasamente soluble y calcular la concentración de una especie dado un potencial medido y las concentraciones de todas las otras especies.