5.6: Ley de Hess - La fisica y quimica

Objetivos de aprendizaje

Usar la ley de Hess y los ciclos termoquímicos para calcular los cambios de entalpía de las reacciones químicas.

Debido a que la entalpía es una función de estado, el cambio de entalpía para una reacción depende solo de dos cosas: (1) las masas de las sustancias que reaccionan y (2) los estados físicos de los reactivos y productos. No depende de la ruta por la cual los reactivos se convierten en productos. Si subió una montaña, por ejemplo, el cambio de altitud no dependerá de si subió todo el camino sin detenerse o si se detuvo muchas veces para tomar un descanso. Si se detuvo a menudo, el cambio general en la altitud sería la suma de los cambios en la altitud para cada tramo corto escalado. De manera similar, cuando agregamos dos o más ecuaciones químicas equilibradas para obtener una ecuación química neta, ΔH para la reacción neta es la suma de los valores de ΔH para las reacciones individuales. Este principio se llama la ley de Hess , en honor al químico ruso nacido en Suiza Germain Hess (1802-1850), pionero en el estudio de la termoquímica. La ley de Hess nos permite calcular los valores de ΔH para reacciones que son difíciles de llevar a cabo directamente al sumar los valores de ΔH conocidos para los pasos individuales que dan la reacción general, a pesar de que la reacción general puede no ocurrir realmente a través de esos pasos.

La Ley de Hess argumenta que ΔH para la reacción neta es la suma de los valores de ΔH para las reacciones individuales. Esto no es más que argumentar que ΔH es una función de estado.

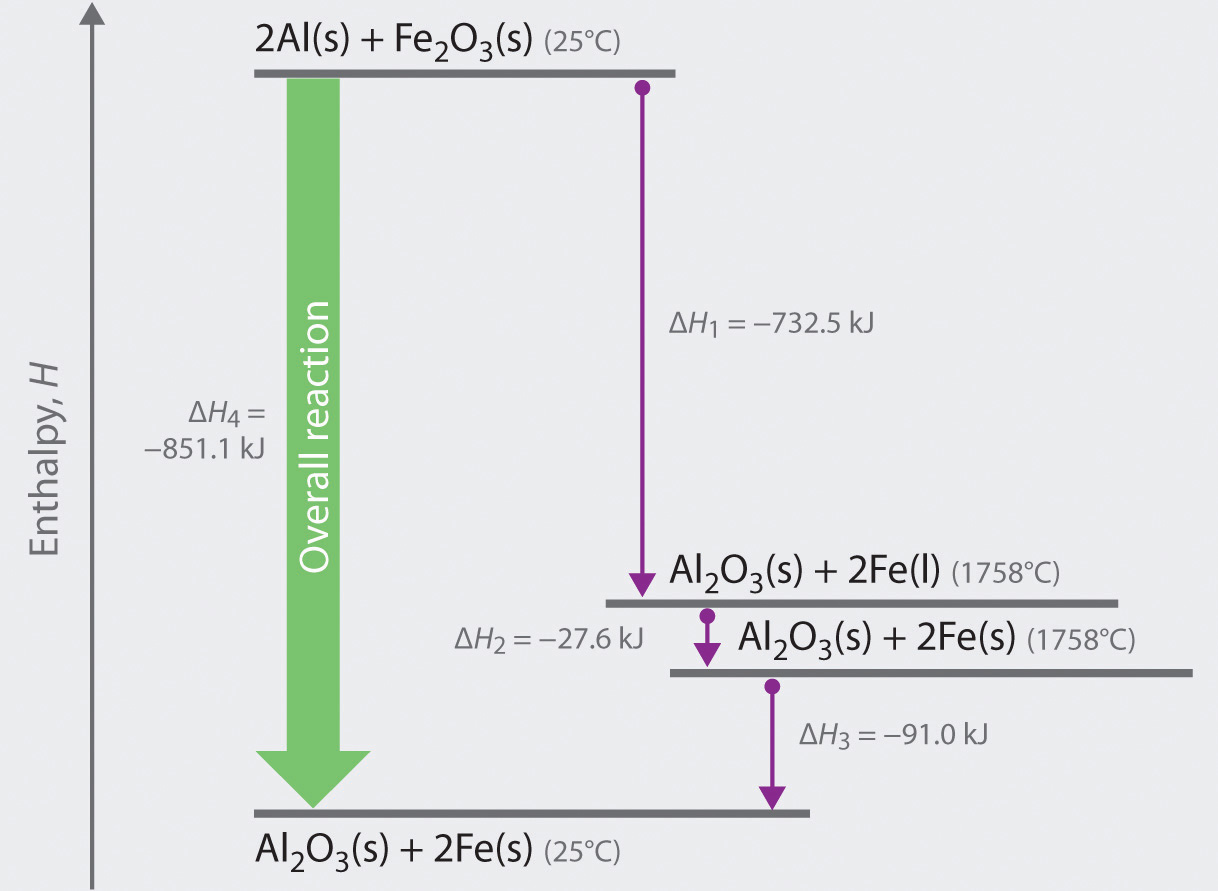
Podemos ilustrar la ley de Hess usando la reacción de termita. La reacción general que se muestra en la Ecuación ( ref {5.6.1} ) puede verse como ocurrida en tres pasos distintos con valores de ΔH conocidos. Como se muestra en la figura 5.6.1, la primera reacción produce 1 mol de óxido de aluminio sólido (Al ₂ O ₃) y 2 mol de hierro líquido en su punto de fusión de 1758 ° C (parte (a) en la ecuación ( ref {5.6.1} )); El cambio de entalpía para esta reacción es -732.5 kJ / mol de Fe ₂ O ₃. La segunda reacción es la conversión de 2 mol de hierro líquido a 1758 ° C en 2 mol de hierro sólido a 1758 ° C (parte (b) en la ecuación 5.6.1); El cambio de entalpía para esta reacción es −13.8 kJ / mol de Fe (−27.6 kJ por 2 mol de Fe). En la tercera reacción, 2 mol de hierro sólido a 1758 ° C se convierten en 2 mol de hierro sólido a 25 ° C (parte (c) en la Ecuación ( ref {5.6.1} )); El cambio de entalpía para esta reacción es -45.5 kJ / mol de Fe (-91.0 kJ por 2 mol de Fe). Como puede ver en la Figura 5.6.1, la reacción general viene dada por la flecha más larga (que se muestra a la izquierda), que es la suma de las tres flechas más cortas (que se muestra a la derecha). Al agregar las partes (a), (b) y (c) en la Ecuación 5.6.1 se obtiene la reacción general, que se muestra en la parte (d):

[ small begin {matrix}
2Al left (s, ; 25 ^ {o} C right) + 2Fe_ {2} O_ {3} left (s, ; 25 ^ {o} C right) & rightarrow & 2Fe left ( l, ; 1758 ^ {o} C right) + 2Al_ {2} O_ {3} left (s, ; 1758 ^ {o} C right) & Delta H = -732.5 ; kJ & left (a right) \
2Fe left (l, ; 1758 ^ {o} C right) & rightarrow & 2Fe left (s, ; 1758 ^ {o} C right) & Delta H = – ; ; 27,6 ; kJ & left (b right) \
2Fe left (s, ; 1758 ^ {o} C right) + 2Al_ {2} O_ {3} left (s, ; 1758 ^ {o} C right) & rightarrow & 2Fe left ( l, ; 25 ^ {o} C right) + 2Al_ {2} O_ {3} left (s, ; 25 ^ {o} C right) & Delta H = – ; ; 91.0 ; kJ & left (c right) \
2Al left (s, ; 25 ^ {o} C right) + 2Fe_ {2} O_ {3} left (s, ; 25 ^ {o} C right) & rightarrow & 2Al_ {2} O_ {3} left (s, ; 25 ^ {o} C right) + 2Fe left (s, ; 25 ^ {o} C right) & Delta H = -851.1 ; kJ & left (d right)
end {matrix} label {5.6.1} ]

La reacción neta en la parte (d) en la ecuación ( ref {5.6.1} ) es idéntica a la ecuación para la reacción de termita que vimos en una sección anterior. Según la ley de Hess, el cambio de entalpía para la parte (d) es la suma de los cambios de entalpía para las partes (a), (b) y (c). En esencia, la ley de Hess nos permite calcular el cambio de entalpía para la suma de una serie de reacciones sin tener que dibujar un diagrama como ese en la Figura ( PageIndex {1} ).

alt — Figura ( PageIndex {1} ): Cambios de energía que acompañan a la reacción de termita. Debido a que la entalpía es una función de estado, el cambio general de la entalpía para la reacción de 2 mol de Al (s) con 1 mol de Fe ₂ O ₃ (s) es −851.1 kJ, si la reacción ocurre en un solo paso (ΔH ₄, que se muestra a la izquierda) o en tres pasos hipotéticos (que se muestran a la derecha) que implican la formación sucesiva de Al sólido ₂ O ₃ y hierro líquido (ΔH ₁), hierro sólido a 1758 ° C (ΔH ₂) y hierro sólido a 25 ° C (ΔH ₃). Así, ΔH ₄ = ΔH ₁ + ΔH ₂ + ΔH ₃, según lo establecido por la ley de Hess.

La comparación de las partes (a) y (d) en la ecuación ( ref {5.6.1} ) también ilustra un punto importante: la magnitud de ΔH para una reacción depende de los estados físicos de los reactivos y los productos ( gas, líquido, sólido o solución). Cuando el producto es hierro líquido en su punto de fusión (parte (a) en la Ecuación ( ref {5.6.1} )), solo se liberan 732.5 kJ de calor a los alrededores en comparación con 852 kJ cuando el producto es hierro sólido a 25 ° C (parte (d) en la ecuación ( ref {5.6.1} )). La diferencia, 120 kJ, es la cantidad de energía que se libera cuando 2 mol de hierro líquido se solidifica y se enfría a 25 ° C. Es importante especificar el estado físico de todos los reactivos y productos al escribir una ecuación termoquímica.

Cuando use la ley de Hess para calcular el valor de ΔH para una reacción, siga este procedimiento:

Identifique la ecuación cuyo valor de ΔH es desconocido y escriba reacciones individuales con valores de ΔH conocidos que, cuando se sumen, darán la ecuación deseada. Ilustramos cómo usar este procedimiento en el Ejemplo ( PageIndex {1} ).

Organice las ecuaciones químicas de modo que la reacción de interés sea la suma de las reacciones individuales.

Si se debe revertir una reacción, cambie el signo de ΔH para esa reacción. Además, si una reacción debe multiplicarse por un factor para obtener el número correcto de moles de una sustancia, multiplique su valor ΔH por ese mismo factor.

Sume las reacciones individuales y sus valores de ΔH correspondientes para obtener la reacción de interés y la ΔH desconocida.

Ejemplo ( PageIndex {1} )

Cuando el carbón se quema con cantidades limitadas de gas oxígeno (O ₂), el producto principal es el monóxido de carbono (CO):

[ left (1 right) ; 2C left (s right) + O_ {2} left (g right) rightarrow 2CO left (g right) ; ; ; Delta H = -221.0 ; kJ ]

Cuando el carbono se quema en exceso O ₂, se produce dióxido de carbono (CO ₂):

[ left (2 right) ; C left (s right) + O_ {2} left (g right) rightarrow CO_ {2} left (g right) ; ; ; Delta H = -393.5 ; kJ ]

Utilice esta información para calcular el cambio de entalpía por mol de CO para la reacción de CO con O ₂ para dar CO ₂.

Dado: dos ecuaciones químicas equilibradas y sus valores de ΔH

Preguntado por: cambio de entalpía para una tercera reacción

Estrategia:

Después de equilibrar la ecuación química para la reacción general, escriba dos ecuaciones cuyos valores de ΔH sean conocidos y que, cuando se sumen, den la ecuación para la reacción general. (Invierta la dirección de una o más de las ecuaciones según sea necesario, asegurándose de invertir también el signo de ΔH.)

Multiplique las ecuaciones por factores apropiados para asegurarse de que den la ecuación química general deseada cuando se suman. Para obtener el cambio de entalpía por mol de CO, escriba las ecuaciones resultantes como una suma, junto con el cambio de entalpía para cada uno.

Solución:

A Comenzamos escribiendo la ecuación química equilibrada para la reacción de interés:

[ left (3 right) ; CO left (g right) + frac {1} {2} O_ {2} left (g right) rightarrow CO_ {2} left (g right) ; ; ; Delta H_ {rxn} =? ]

Hay al menos dos formas de resolver este problema utilizando la ley de Hess y los datos proporcionados. Lo más simple es escribir dos ecuaciones que se puedan sumar para obtener la ecuación deseada y para la cual se conocen los cambios de entalpía. Observando que el CO, un reactivo en la Ecuación 3, es un producto en la Ecuación 1, podemos revertir la Ecuación (1) para dar

[2CO left (g right) rightarrow 2C left (s right) + O_ {2} left (g right) ; ; ; Delta H = + 221.0 ; kJ ]

Debido a que hemos invertido la dirección de la reacción, se cambia el signo de ΔH. Podemos usar la Ecuación 2 como está escrita porque su producto, CO ₂, es el producto que queremos en la Ecuación 3:

[C left (s right) + O_ {2} left (g right) rightarrow CO_ {2} left (s right) ; ; ; Delta H = -393.5 ; kJ ]

B Agregar estas dos ecuaciones juntas no da la reacción deseada, sin embargo, porque los números de C (s) en los lados izquierdo y derecho no se cancelan. De acuerdo con nuestra estrategia, podemos multiplicar la segunda ecuación por 2 para obtener 2 mol de C (s) como reactivo:

[2C left (s right) + 2O_ {2} left (g right) rightarrow 2CO_ {2} left (s right) ; ; ; Delta H = -787.0 ; kJ ]

Al escribir las ecuaciones resultantes como una suma, junto con el cambio de entalpía para cada una, se obtiene

[ begin {matrix}
2CO left (g right) & rightarrow & cancel {2C left (s right)} + cancel {O_ {2} left (g right)} & Delta H & = & – Delta H_ {1} & = & +221.0 ; kJ \
cancel {2C left (s right)} + cancel {2} O_ {2} left (g right) & rightarrow & 2CO_ {2} left (g right) & Delta H & = & – Delta 2H_ {2} & = & -787.0 ; kJ \
2CO left (g right) + O_ {2} left (g right) & rightarrow & 2CO_ {2} left (g right) & Delta H & = & & -566.0 ; kJ
end {matriz} ]

Tenga en cuenta que la ecuación química general y el cambio de entalpía para la reacción son para la reacción de 2 mol de CO con O ₂, y el problema requiere la cantidad por mol de CO. En consecuencia, debemos dividir ambos lados de la ecuación final y la magnitud de ΔH por 2:

[ begin {matrix}
CO left (g right) + frac {1} {2} O_ {2} left (g right) & rightarrow & CO_ {2} left (g right) & Delta H & = & & -283.0 ; kJ
end {matriz} ]

Una forma alternativa e igualmente válida de resolver este problema es escribir las dos ecuaciones dadas como que ocurren en pasos. Tenga en cuenta que hemos multiplicado las ecuaciones por los factores apropiados para permitirnos cancelar los términos:

( small begin {matrix}
left (A right) & 2C left (s right) + O_ {2} left (g right) & rightarrow & cancel {2CO left (g right)} & Delta H_ {A } & = & Delta H_ {1} & = & +221.0 ; kJ \
left (B right) & cancel {2CO left (g right)} + O_ {2} left (g right) & rightarrow & 2CO_ {2} left (g right) & Delta H_ {B} & & & = &? \
left (C right) & 2C left (s right) + 2O_ {2} left (g right) & rightarrow & 2CO_ {2} left (g right) & Delta H & = 2 Delta H_ {2} & = 2 times left (-393.5 ; kJ right) & = -787.0 ; kJ
end {matrix} )

La suma de las reacciones A y B es la reacción C, que corresponde a la combustión de 2 mol de carbono para dar CO ₂. Según la ley de Hess, ΔH _A + ΔH _B = ΔH _C, y se nos da ΔH para las reacciones A y C. La sustitución de los valores apropiados da

[ begin {matrix}
-221.0 ; kJ + Delta H_ {B} = -787.0 ; kJ \
Delta H_ {B} = -566.0
end {matriz} ]

Este es nuevamente el cambio de entalpía para la conversión de 2 mol de CO a CO ₂. El cambio de entalpía para la conversión de 1 mol de CO a CO ₂ es, por lo tanto, −566.0 ÷ 2 = −283.0 kJ / mol de CO, que es el mismo resultado que obtuvimos anteriormente. Como puede ver, puede haber más de una forma correcta de resolver un problema.

Ejercicio ( PageIndex {1} )

La reacción de acetileno (C ₂ H ₂) con hidrógeno (H ₂) puede producir etileno (C ₂ H ₄) o etano (C ₂ H ₆):

[ begin {matrix}
C_ {2} H_ {2} left (g right) + H_ {2} left (g right) rightarrow C_ {2} H_ {4} left (g right) & Delta H = – 175,7 ; kJ / mol ; C_ {2} H_ {2} \
C_ {2} H_ {2} left (g right) + 2H_ {2} left (g right) rightarrow C_ {2} H_ {6} left (g right) & Delta H = – 312.0 ; kJ / mol ; C_ {2} H_ {2}
end {matriz} ]

¿Cuál es ΔH para la reacción de C ₂ H ₄ con H ₂ para formar C ₂ H ₆

Respuesta

−136,3 kJ / mol de C ₂ H ₄

Tabla de contenidos

Resumen

La ley de Hess está argumentando que el cambio general de entalpía para una serie de reacciones es la suma de los cambios de entalpía para las reacciones individuales. Para una reacción química, la entalpía de reacción (Δ H _rxn ) es la diferencia en la entalpía entre productos y reactivos ; las unidades de ΔH _rxn son kilojulios por mol. Revertir una reacción química invierte el signo de ΔH _rxn. La magnitud de ΔH _rxn también depende del estado físico de los reactivos y los productos porque los procesos como la fusión de sólidos o líquidos de vaporización también van acompañados de cambios de entalpía: la entalpía de fusión (Δ ] H _fus ) y la entalpía de vaporización (Δ H _vap [ 19459030]) , respectivamente. El cambio general de entalpía para una serie de reacciones es la suma de los cambios de entalpía para las reacciones individuales, que es la ley de Hess . La entalpía de combustión (Δ H _peine ) es el cambio de entalpía que ocurre cuando una sustancia se quema en exceso de oxígeno.

Colaboradores

Modificado por Joshua Halpern ( Universidad de Howard )

Post Views: 13