Objetivos de aprendizaje
- Para comprender las entalpías de formación y poder usarlas para calcular las entalpías de reacción
Una forma de informar el calor absorbido o liberado por las reacciones químicas sería compilar un conjunto masivo de tablas de referencia que enumeren los cambios de entalpía para todas las reacciones químicas posibles, lo que requeriría una increíble cantidad de esfuerzo. Afortunadamente, la ley de Hess nos permite calcular el cambio de entalpía para prácticamente cualquier reacción química concebible utilizando un conjunto relativamente pequeño de datos tabulados, comenzando por las formas elementales de cada átomo a 25 o C y 1 atm de presión.
La entalpía de formato ion ( (ΔH_f )) es el cambio de entalpía para la formación de 1 mol de un compuesto a partir de sus elementos componentes, como la formación de dióxido de carbono a partir de carbono y oxígeno. La relación correspondiente es
[elements rightarrow compuesto ; ; ; ; Delta H_ {rxn} = Delta H_ {f} label {7.8.1} ]
Por ejemplo, considere la combustión de carbono:
[ ce {C (s) + O2 (g) -> CO2 (g)}
onumber ]
luego
[ Delta H_ {rxn} = Delta H_ {f} left [CO_ {2} left (g right) right]
onumber ]
La convención de signos para Δ H f es la misma que para cualquier cambio de entalpía: (ΔH_f <0 ) si se libera calor cuando los elementos se combinan para formar un compuesto y (ΔH_f> 0 ) si se absorbe calor.
La convención de signos es la misma para todos los cambios de entalpía: negativa si el sistema libera calor y positiva si el sistema absorbe calor.
Entalpías estándar de formación
La magnitud de Δ H para una reacción depende de los estados físicos de los reactivos y los productos (gas, líquido, sólido o solución), la presión de cualquier gas presente y la temperatura a cual la reacción se lleva a cabo. Para evitar la confusión causada por las diferencias en las condiciones de reacción y garantizar la uniformidad de los datos, la comunidad científica ha seleccionado un conjunto específico de condiciones bajo las cuales se miden los cambios de entalpía. Estas condiciones estándar sirven como punto de referencia para medir las diferencias en la entalpía, al igual que el nivel del mar es el punto de referencia para medir la altura de una montaña o para informar la altitud de un avión.
Las condiciones estándar para las cuales se tabulan la mayoría de los datos termoquímicos son una presión de 1 atmósfera (atm) para todos los gases y una concentración de 1 M para Todas las especies en solución (1 mol / L). Además, cada sustancia pura debe estar en su estado estándar , que suele ser su forma más estable a una presión de 1 atm a una temperatura especificada. Suponemos una temperatura de 25 ° C (298 K) para todos los cambios de entalpía dados en este texto, a menos que se indique lo contrario. Las entalpías de formación medidas en estas condiciones se denominan entalpías estándar de formación ( (ΔH ^ o_f ) ) El cambio de entalpía para la formación de 1 mol de un compuesto de sus elementos componentes cuando los elementos componentes están cada uno en sus estados estándar. La entalpía estándar de formación de cualquier elemento en su forma más estable es cero por definición.
La entalpía estándar de formación de cualquier elemento en su estado estándar es cero por definición.
Por ejemplo, aunque el oxígeno puede existir como ozono (O 3 ), oxígeno atómico (O) y oxígeno molecular (O 2 ), O 2 [19459025 ] es la forma más estable a 1 atm de presión y 25 ° C. De manera similar, el hidrógeno es H 2 (g), no hidrógeno atómico (H). El grafito y el diamante son formas de carbono elemental, pero como el grafito es más estable a una presión de 1 atm y 25 ° C, el estado estándar del carbono es el grafito (Figura ( PageIndex {1} )). Por lo tanto, ( ce {O2 (g)} ), ( ce {H2 (g)} ) y el grafito tienen valores de (ΔH ^ o_f ) de cero.

La entalpía estándar de formación de glucosa a partir de los elementos a 25 ° C es el cambio de entalpía para la siguiente reacción:
[6C left (s, grafito right) + 6H_ {2} left (g right) + 3O_ {2} left (g right) rightarrow C_ {6} H_ {12} O_ {6} left (s right) ; ; ; Delta H_ {f} ^ {o} = – 1273.3 ; kJ label {7.8.2} ]
No es posible medir el valor de ΔH o f para glucosa, −1273.3 kJ / mol, simplemente mezclando cantidades apropiadas de grafito, O 2 y H 2 y midiendo el calor evolucionado a medida que se forma la glucosa; la reacción que se muestra en la Ecuación ( ref {7.8.2} ) no ocurre a una velocidad medible bajo ninguna condición conocida. La glucosa no es única; La mayoría de los compuestos no pueden prepararse mediante las ecuaciones químicas que definen sus entalpías estándar de formación. En cambio, los valores de se obtienen utilizando la ley de Hess y los cambios de entalpía estándar que se han medido para otras reacciones, como las reacciones de combustión. Los valores de (ΔH ^ o_f ) para una extensa lista de compuestos se dan en Tabla T1 . Tenga en cuenta que los valores de (ΔH ^ o_f ) siempre se informan en kilojulios por mol de la sustancia de interés. Observe también en Tabla T1 que la entalpía estándar de formación de O 2 (g) es cero porque es la forma más estable de oxígeno en su estado estándar.
Ejemplo ( PageIndex {1} ): Entalpía de formación
Para la formación de cada compuesto, escriba una ecuación química equilibrada correspondiente a la entalpía estándar de formación de cada compuesto.
- ( ce {HCl (g)} )
- ( ce {MgCO3 (s)} )
- ( ce {CH3 (CH2) 14CO2H (s)} ) ( ácido palmítico )
- Dado:
-
fórmula compuesta y fase.
- Preguntado por:
-
ecuación química equilibrada para su formación a partir de elementos en estados estándar
- Estrategia:
-
Utilice Tabla T1 para identificar el estado estándar de cada elemento. Escriba una ecuación química que describa la formación del compuesto a partir de los elementos en sus estados estándar y luego equilibre para que se forme 1 mol de producto.
- Solución:
-
Para calcular la entalpía estándar de formación de un compuesto, debemos comenzar con los elementos en sus estados estándar. El estado estándar de un elemento se puede identificar en Tabla T1 : por un valor ΔH o f de 0 kJ / mol.
El cloruro de hidrógeno contiene un átomo de hidrógeno y un átomo de cloro. Debido a que los estados estándar de hidrógeno elemental y cloro elemental son H 2 (g) y Cl 2 (g), respectivamente, la ecuación química desequilibrada es
[ ce {H2 (g) + Cl2 (g) Hightarrow HCl (g)}
onumber ]Se requieren coeficientes fraccionarios en este caso porque ΔH o f los valores se informan para 1 mol del producto, ( ce {HCl} ). Multiplicar tanto ( ce {H2 (g)} ) como ( ce {Cl2 (g)} ) por 1/2 equilibra la ecuación:
[ ce { dfrac {1} {2} H_ {2} (g) + dfrac {1} {2} Cl_ {2} (g) Hightarrow HCl (g)}
onumber ]Los estados estándar de los elementos en este compuesto son ( ce {Mg (s)} ), ( ce {C (s, grafito)} ) y ( ce {O2 (g )} ). La ecuación química desequilibrada es, por lo tanto,
[ ce {Mg (s) + C (s, grafito) + O2 (g) MgCO3 de la derecha / s}
onumber ]Esta ecuación se puede equilibrar mediante inspección para dar
[ ce {Mg (g) + C (s, grafito) + dfrac {3} {2} O2 (g) rightarrow MgCO3 (s)}
onumber ]El ácido palmítico, la grasa principal en la carne y los productos lácteos, contiene hidrógeno, carbono y oxígeno, por lo que la ecuación química desequilibrada para su formación a partir de los elementos en sus estados estándar es la siguiente: [ ce {C (s , grafito) + H2 (g) + O2 (g) rightarrow CH3 (CH2) 14CO2H (s)}
onumber ]Hay 16 átomos de carbono y 32 átomos de hidrógeno en 1 mol de ácido palmítico, por lo que la ecuación química equilibrada es
[ ce {16C (s, grafito) + 16 H2 (g) + O2 (g) -> CH3 (CH2) 14CO2H (s)}
onumber ]
Ejercicio ( PageIndex {1} )
Para la formación de cada compuesto, escriba una ecuación química equilibrada correspondiente a la entalpía estándar de formación de cada compuesto.
- ( ce {NaCl (s)} )
- ( ce {H2SO4 (l)} )
- ( ce {CH3CO2H (l)} ) ( ácido acético )
- Responda a
-
[ ce {Na (s) + dfrac {1} {2} Cl2 (g) NaCl (s) de rightarrow}
onumber ] - Respuesta b
-
[ ce {H_ {2} (g) + dfrac {1} {8} S8 (s) + 2O2 (g) rightarrow H2 SO4 (l)}
onumber ] - Respuesta c
-
[ ce {2C (s) + O2 (g) + 2H2 (g) -> CH3CO2H (l)}
onumber ]
Entalpías de reacción estándar
Los valores tabulados de entalpías de formación estándar se pueden usar para calcular los cambios de entalpía para cualquier reacción que involucre sustancias cuyos valores ( Delta {H_f ^ o} ) son conocidos. La entalpía de reacción estándar ( Delta {H_ {rxn} ^ o} ) es el cambio de entalpía que ocurre cuando una reacción se lleva a cabo con todos los reactivos y productos en sus estados estándar. Considere la reacción general
[aA + bB rightarrow cC + dD label {7.8.3} ]
donde A, B, C y D son sustancias químicas y a , b , c y d son sus coeficientes estequiométricos. La magnitud de (ΔH ^ ο ) es la suma de las entalpías estándar de formación de los productos, cada una multiplicada por su coeficiente apropiado, menos la suma de las entalpías estándar de formación de los reactivos, también multiplicada por sus coeficientes: [ 19459005]
[ Delta H_ {rxn} ^ {o} = underbrace { left [c Delta H_ {f} ^ {o} left (C right) + d Delta H_ {f} ^ { o} left (D right) right]} _ { text {products}} – underbrace { left [a Delta H_ {f} ^ {o} left (A right) + b Delta H_ {f} ^ {o} left (B right) right]} _ { text {reactants}} label {7.8.4} ]
Más generalmente, podemos escribir
[ Delta H_ {rxn} ^ {o} = sum m Delta H_ {f} ^ {o} left (productos right) – sum n Delta H_ {f} ^ {o} left (reactivos right) label {7.8.5} ]
donde el símbolo ( sum ) significa “suma de” y m y n son los coeficientes estequiométricos de cada uno de los productos y los reactivos, respectivamente. Las sumaciones de “productos menos reactivos” como la ecuación ( ref {7.8.5} ) surgen del hecho de que la entalpía es una función de estado. Debido a que muchas otras cantidades termoquímicas también son funciones de estado, las sumas de “productos menos reactivos” son muy comunes en química; nos encontraremos con muchos otros en capítulos posteriores.
Las sumaciones de “productos menos reactivos” son típicas de las funciones de estado.
Para demostrar el uso de valores tabulados ΔH ο , los usaremos para calcular (ΔH_ {rxn} ) para la combustión de glucosa, la reacción que proporciona energía para tu cerebro:
[C_ {6} H_ {12} O_ {6} left (s right) + 6O_ {2} left (g right) rightarrow 6CO_ {2} left (g right) + 6H_ {2} O left (l right) label {7.8.6} ]
Usando la ecuación ( ref {7.8.5} ), escribimos
[ Delta H_ {f} ^ {o} = left {6 Delta H_ {f} ^ {o} left [CO_ {2} left (g right) right] + 6 Delta H_ {f} ^ {o} left [H_ {2} O left (g right) right] right } – left { Delta H_ {f} ^ {o} left [ C_ {6} H_ {12} O_ {6} left (s right) right] + 6 Delta H_ {f} ^ {o} left [O_ {2} left (g right) right ] right } label {7.8.7} ]
De Tabla T1 , los valores relevantes ΔH o f son ΔH ο [ 19459044] f [CO 2 (g)] = – 393.5 kJ / mol , ΔH ο [ 19459015] f [H 2 O (l)] = – 285,8 kJ / mol y ΔH ο f [C 6 H 12 O 6 [19459062 ] (s) ] = – 1273,3 kJ / mol . Debido a que O 2 (g) es un elemento puro en su estado estándar, ΔH ο f [O 2 (g) ] = 0 kJ / mol. Al insertar estos valores en la ecuación ( ref {7.8.7} ) y cambiar el subíndice para indicar que se trata de una reacción de combustión, obtenemos
[ begin {matrix} Delta H_ {comb} ^ {o} = left [6 left (-393.5 ; kJ / mol right) + 6 left (-285.8 ; kJ / mol right) right] \ – left [-1273.3 + 6 left (0 ; kJ ; mol right) right] = -2802.5 ; kJ / mol end {matriz} etiqueta {7.8.8} ]
Como se ilustra en la Figura ( PageIndex {2} ), podemos usar la Ecuación ( ref {7.8.8} ) para calcular (ΔH ^ ο_f ) para glucosa porque la entalpía es una función de estado. La figura muestra dos vías desde los reactivos (centro a la izquierda) hasta los productos (abajo). La ruta más directa es la flecha verde hacia abajo etiquetada (ΔH ^ ο_ {comb} ). La vía hipotética alternativa consiste en cuatro reacciones separadas que convierten los reactivos en los elementos en sus estados estándar (flecha morada hacia arriba a la izquierda) y luego convierten los elementos en los productos deseados (flechas moradas hacia abajo a la derecha). Las reacciones que convierten los reactivos en los elementos son el reverso de las ecuaciones que definen los valores (ΔH ^ ο_f ) de los reactivos. En consecuencia, los cambios de entalpía son
[ begin {align} Delta H_ {1} ^ {o} & = Delta H_ {f} ^ {o} left [glucosa left (s right) right]
onumber \ [4pt] & = -1 ; cancel {mol ; glucosa} left ( dfrac {1273.3 ; kJ} {1 ; cancel {mol ; glucosa}} right)
onumber \ [4pt] & = +1273.3 ; kJ
onumber \ [4pt] Delta H_ {2} ^ {o} & = 6 Delta H_ {f} ^ {o} left [O_ {2} left (g right) right]
onumber \ [4pt] & = 6 ; cancel {mol ; O_ {2}} left ( dfrac {0 ; kJ} {1 ; cancel {mol ; O_ {2}}} right)
onumber \ [4pt] & = 0 ; kJ end {align} label {7.8.9} ]
Recuerde que cuando revertimos una reacción, también debemos revertir el signo del cambio de entalpía que lo acompaña (Ecuación ref {7.8.4} ya que los productos ahora son reactivos y viceversa.
El cambio global de entalpía para la conversión de los reactivos (1 mol de glucosa y 6 mol de O 2 ) a los elementos es, por lo tanto, +1273.3 kJ.
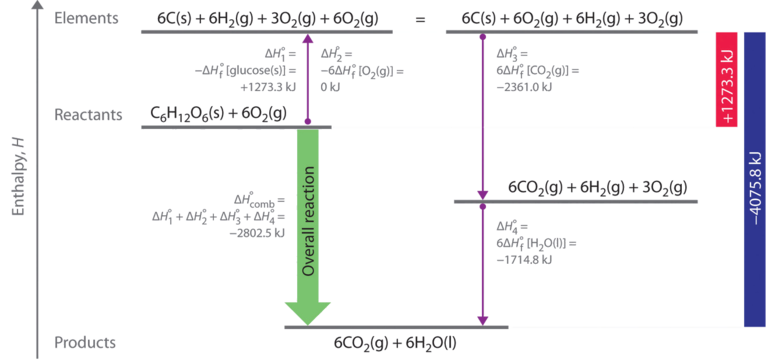
Las reacciones que convierten los elementos en productos finales (flechas moradas hacia abajo en la Figura ( PageIndex {2} )) son idénticas a las utilizadas para definir el ΔH o f valores de los productos. En consecuencia, los cambios de entalpía (de Tabla T1 ) son
[ begin {matrix} Delta H_ {3} ^ {o} = Delta H_ {f} ^ {o} left [CO_ {2} left (g right) right] = 6 ; cancel {mol ; CO_ {2}} left ( dfrac {393.5 ; kJ} {1 ; cancel {mol ; CO_ {2}}} right) = -2361.0 ; kJ \ Delta H_ {4} ^ {o} = 6 Delta H_ {f} ^ {o} left [H_ {2} O left (l right) right] = 6 ; cancel {mol ; H_ {2} O} left ( dfrac {-285.8 ; kJ} {1 ; cancel {mol ; H_ {2} O}} right) = -1714.8 ; kJ end {matriz} ]
El cambio global de entalpía para la conversión de los elementos en productos (6 mol de dióxido de carbono y 6 mol de agua líquida) es, por lo tanto, -4075.8 kJ. Debido a que la entalpía es una función de estado, la diferencia en la entalpía entre un estado inicial y un estado final se puede calcular utilizando cualquier vía que conecte los dos. Así, el cambio de entalpía para la combustión de glucosa en dióxido de carbono y agua es la suma de los cambios de entalpía para la conversión de glucosa y oxígeno en los elementos (+1273.3 kJ) y para la conversión de los elementos en dióxido de carbono y agua (- 4075.8 kJ):
[ Delta H_ {comb} ^ {o} = +1273.3 ; kJ + left (-4075.8 ; kJ right) = -2802.5 ; kJ label {7.8.10} ]
Este es el mismo resultado que obtuvimos usando la regla “productos menos reactivos” (Ecuación ( ref {7.8.5} )) y ΔH o f [19459025 ] valores. Los dos resultados deben ser los mismos porque la Ecuación ( ref {7.8.10} ) es solo una forma más compacta de describir el ciclo termoquímico que se muestra en la Figura ( PageIndex {1} ).
Ejemplo ( PageIndex {2} ): Calor de combustión
Los ácidos grasos de cadena larga como el ácido palmítico ( ( ce {CH3 (CH2) 14CO2H} )) son una de las dos principales fuentes de energía en nuestra dieta ( (ΔH ^ o_f ) = −891.5 kJ / mol). Use los datos en Tabla T1 para calcular ΔH ο peine para la combustión de ácido palmítico. Según la energía liberada en la combustión por gramo , ¿cuál es el mejor combustible: glucosa o ácido palmítico?
Dado: valores compuestos y (ΔH ^ ο_ {f} )
Preguntado por: (ΔH ^ ο_ {comb} ) por mol y por gramo
Estrategia:
- Después de escribir la ecuación química balanceada para la reacción, use la Ecuación ( ref {7.8.5} ) y los valores de Tabla T1 para calcular (ΔH ^ ο_ {comb} ) La energía liberada por la combustión de 1 mol de ácido palmítico.
- Divida este valor por la masa molar de ácido palmítico para encontrar la energía liberada por la combustión de 1 g de ácido palmítico. Compare este valor con el valor calculado en la Ecuación ( ref {7.8.8} ) para la combustión de glucosa para determinar cuál es el mejor combustible.
Solución:
A Para determinar la energía liberada por la combustión del ácido palmítico, necesitamos calcular su (ΔH ^ ο_f ). Como siempre, el primer requisito es una ecuación química equilibrada:
[C_ {16} H_ {32} O_ {2 (s)} + 23O_ {2 (g)} rightarrow 16CO_ {2 (g)} + 16H_2O _ {(l)}
onumber ]
Usando la ecuación ( ref {7.8.5} ) (“productos menos reactivos”) con ΔH ο f valores de La Tabla T1 (y omitiendo los estados físicos de los reactivos y productos para ahorrar espacio) da
[ begin {align *} Delta H_ {comb} ^ {o} & = sum m Delta {H ^ o} _f left ({productos} right) – sum n Delta { H ^ o} _f left ({reactivos} right) \ [4pt] & = left [16 left (-393.5 ; kJ / mol ; CO_ {2} right) + 16 left (- 285.8 ; kJ / mol ; H_ {2} O ; right) right] \ [4pt] & – left [-891.5 ; kJ / mol ; C_ {16} H_ {32} O_ {2} + 23 izquierda (0 ; kJ / mol ; O_ {2} ; derecha) derecha] \ [4pt] & = -9977.3 ; kJ / mol
onumber end {align *} ]
Esta es la energía liberada por la combustión de 1 mol de ácido palmítico.
B La energía liberada por la combustión de 1 g de ácido palmítico es
( Delta H_ {comb} ^ {o} ; per ; gram = left ( dfrac {9977.3 ; kJ} { cancel {1 ; mol}} right) left ( dfrac { cancel {1 ; mol}} {256.42 ; g} right) = -38.910 ; kJ / g
onumber )
Según lo calculado en la Ecuación ( ref {7.8.8} ), ΔH ο f de glucosa es −2802.5 kJ / mol. La energía liberada por la combustión de 1 g de glucosa es, por lo tanto,
( Delta H_ {comb} ^ {o} ; per ; gram = left ( dfrac {-2802.5 ; kJ} { cancel {1 ; mol}} right) left ( dfrac { cancel {1 ; mol}} {180.16 ; g} right) = -15.556 ; kJ / g
onumber )
La combustión de grasas como el ácido palmítico libera más del doble de energía por gramo que la combustión de azúcares como la glucosa. Esta es una razón por la que muchas personas intentan minimizar el contenido de grasa en sus dietas para perder peso.
Ejercicio ( PageIndex {2} ): reacción de cambio de agua-gas
Utilice Tabla T1 para calcular (ΔH ^ o_ {rxn} ) para la reacción de cambio de agua-gas , que se utiliza industrialmente en una escala enorme para obtener H [ 19459024] 2 (g):
[ ce {CO (g) + H2O (g) -> CO2 (g) + H2 (g)}
onumber ]
- Respuesta
-
−41,2 kJ / mol
También podemos medir el cambio de entalpía para otra reacción, como una reacción de combustión, y luego usarlo para calcular el (ΔH ^ ο_f ) de un compuesto que no podemos obtener de otra manera. Este procedimiento se ilustra en el Ejemplo ( PageIndex {3} ).
Ejemplo ( PageIndex {3} ): tetraetilo de plomo
A partir de 1923, tetraethyllead [ ( ce {(C2H5) 4Pb} )] se utilizó como aditivo antidetonante en la gasolina en los Estados Unidos. Su uso se eliminó por completo en 1986 debido a los riesgos para la salud asociados con la exposición crónica al plomo. El tetraetilo es un líquido incoloro altamente venenoso que arde en el aire para dar una llama naranja con un halo verde. Los productos de combustión son ( ce {CO2 (g)} ), ( ce {H2O (l)} ) y rojo ( ce {PbO (s)} ). ¿Cuál es la entalpía estándar de formación de tetraetileno? Dado que (ΔH ^ ο_f ) es −19.29 kJ / g para la combustión de tetraetilo y (ΔH ^ ο_f ) de PbO rojo (s) es −219.0 kJ / mol ?
Dado: reactivo, productos y valores de (ΔH ^ ο_ {comb} )
Preguntado por: (ΔH ^ ο_f ) de los reactivos
Estrategia:
- Escribe la ecuación química balanceada para la combustión de tetraetilo de plomo. Luego inserte las cantidades apropiadas en la Ecuación ( ref {7.8.5} ) para obtener la ecuación para ΔH ο f de tetraetilo de plomo.
- Convierta (ΔH ^ ο_ {comb} ) por gramo dado en el problema a (ΔH ^ ο_ {comb} ) por mol multiplicando (ΔH ^ ο_ {comb} ) por gramo por el molar masa de tetraetileno
- Use Tabla T1 para obtener valores de (ΔH ^ ο_f ) para los otros reactivos y productos. Inserte estos valores en la ecuación para (ΔH ^ ο_f ) de tetraetilo de plomo y resuelva la ecuación.
Solución:
A La ecuación química equilibrada para la reacción de combustión es la siguiente:
[ ce {2 (C2H5) 4Pb (l) + 27O2 (g) → 2PbO (s) + 16CO2 (g) + 20H2O (l)} ]
Usando la ecuación ( ref {7.8.5} ) da
[ Delta H_ {comb} ^ {o} = left [2 Delta H_ {f} ^ {o} left (PbO right) + 16 Delta H_ {f} ^ {o} left (CO_ {2} right) + 20 Delta H_ {f} ^ {o} left (H_ {2} O right) right] – left [2 Delta H_ {f} ^ {o} left ( left (C_ {2} H_ {5} right) _ {4} Pb right) + 27 Delta H_ {f} ^ {o} left (O_ {2} right) right]
onumber ]
Resolviendo para (ΔH ^ o_f [ ce {(C2H5) 4Pb}] ) dar s
[ Delta H_ {f} ^ {o} left ( left (C_ {2} H_ {5} right) _ {4} Pb right) = Delta H_ {f} ^ {o } left (PbO right) + 8 Delta H_ {f} ^ {o} left (CO_ {2} right) + 10 Delta H_ {f} ^ {o} left (H_ {2} O right) – dfrac {27} {2} Delta H_ {f} ^ {o} left (O_ {2} right) – dfrac { Delta H_ {comb} ^ {o}} {2}
onumber ]
Los valores de todos los términos que no sean (ΔH ^ o_f [ ce {(C2H5) 4Pb}] ) se dan en Tabla T1 .
B La magnitud de (ΔH ^ o_ {comb} ) se da en el problema en kilojulios por gramo de tetraetilo de plomo. Por lo tanto, debemos multiplicar este valor por la masa molar de tetraetilo de plomo (323.44 g / mol) para obtener (ΔH ^ o_ {comb} ) para 1 mol de tetraetilo de plomo:
( Delta H_ {comb} ^ {o} = left ( dfrac {-1929 ; kJ} { cancel {g}} right) left ( dfrac {323.44 ; cancel { g}} {mol} right) = -6329 ; kJ / mol
onumber )
Debido a que la ecuación química balanceada contiene 2 mol de tetraetileno, (ΔH ^ o_ {rxn} ) es
[ Delta H_ {rxn} ^ {o} = 2 ; cancel {mol ; left (C_ {2} H {5} right) _4 Pb} left ( dfrac {-6329 ; kJ} {1 ; cancel {mol ; left (C_ {2} H {5} right) _4 Pb}} right) = -12,480 ;
onumber kJ
onumber ]
C Al insertar los valores apropiados en la ecuación para (ΔH ^ o_f [ ce {(C2H5) 4Pb}] ) da
[ begin {matrix}
Delta H_ {f} ^ {o} left [ left (C_ {2} H_ {4} right) _ {4} Pb right] & = & left [1 ; mol ; PbO ; times 219.0 ; kJ / mol right] + left [8 ; mol ; CO_ {2} times left (-393.5 ; kJ / mol right) right] \
& & + left [10 ; mol ; H_ {2} O times left (-285.8 ; kJ / mol right) right] + left [-27/2 ; mol ; O_ {2}) veces 0 ; kJ / mol ; O_ {2} right] \
& & left [12,480.2 ; kJ / mol ; left (C_ {2} H_ {5} right) _ {4} Pb right] \
& = & -219.0 ; kJ -3148 ; kJ – 2858 kJ – 0 kJ + 6240 ; kJ = 15 kJ / mol
end {matriz}
onumber ]
Ejercicio ( PageIndex {3} )
El sulfato de amonio, ( ce {(NH4) 2SO4} ), se utiliza como retardante de fuego y conservante de la madera; se prepara industrialmente por la reacción altamente exotérmica de amoníaco gaseoso con ácido sulfúrico:
[ ce {2NH3 (g) + H2SO4 (aq) rightarrow (NH4) 2SO4 (s)}
onumber ]
El valor de ΔH o rxn es -179,4 kJ / g ( ce { H2SO4} ). Utilice los datos en Tabla T1 para calcular la entalpía estándar de formación de sulfato de amonio (en kilojulios por mol).
- Respuesta
-
−1181 kJ / mol
Resumen
- El estado estándar para medir e informar entalpías de formación o reacción es 25 o C y 1 atm.
- La forma elemental de cada átomo es aquella con la entalpía más baja en el estado estándar.
- El calor de formación del estado estándar para la forma elemental de cada átomo es cero.
La entalpía de formación (Δ H f ) es el cambio de entalpía que acompaña a la formación de un compuesto a partir de sus elementos. Entalpías estándar de formación ( Δ H o f ] ) se determinan bajo condiciones estándar : una presión de 1 atm para gases y una concentración de 1 M para especies en solución, con todas las sustancias puras presentes en sus estados estándar (sus formas más estables a 1 atm de presión y la temperatura de la medición). El calor de formación estándar de cualquier elemento en su forma más estable se define como cero. La entalpía de reacción estándar ( Δ H o ] r xn ) can be calculated from the sum of the standard enthalpies of formation of the products ( each multiplied by its stoichiometric coefficient) minus the sum of the standard enthalpies of formation of the reactants (each multiplied by its stoichiometric coefficient)—the “products minus reactants” rule. The enthalpy of solution (Δ H s oln ) is the heat released or absorbed when a specified amount of a solute dissolves in a certain quantity of solvent at constant pressure.
Contributors
-
Modified by Joshua Halpern ( Howard University )