El concepto del fotón surgió de la experimentación con radiación térmica , radiación electromagnética emitida como resultado de la temperatura de una fuente, que produce un espectro continuo de energías. El efecto fotoeléctrico proporcionó evidencia indiscutible de la existencia de el fotón y, por lo tanto, el comportamiento similar a las partículas de la radiación electromagnética. Sin embargo, se necesitaba más evidencia directa para verificar la naturaleza cuantificada de la energía en toda la materia. En esta sección, describimos cómo la observación de la interacción de los átomos con la luz visible proporcionó esta evidencia.
Espectros de línea
Aunque los objetos a alta temperatura emiten un espectro continuo de radiación electromagnética, se observa un tipo diferente de espectro cuando se calientan muestras puras de elementos individuales. Por ejemplo, cuando se pasa una descarga eléctrica de alto voltaje a través de una muestra de gas hidrógeno a baja presión, los átomos de hidrógeno aislados individuales resultantes causados por la disociación de H 2 emiten una luz roja. A diferencia de la radiación de cuerpo negro, el color de la luz emitida por los átomos de hidrógeno no depende en gran medida de la temperatura del gas en el tubo. Cuando la luz emitida pasa a través de un prisma, solo se observan unas pocas líneas estrechas de longitudes de onda particulares, llamadas espectro de línea, en lugar de un rango continuo de longitudes de onda (Figura ( PageIndex {1} )). La luz emitida por los átomos de hidrógeno es roja porque, de sus cuatro líneas características, la línea más intensa en su espectro está en la porción roja del espectro visible, a 656 nm. Con sodio, sin embargo, observamos un color amarillo porque las líneas más intensas en su espectro están en la porción amarilla del espectro, a aproximadamente 589 nm.


Tales espectros de emisión se observaron para muchos otros elementos a fines del siglo XIX, lo que representaba un gran desafío porque la física clásica no podía explicarlos. Parte de la explicación es proporcionada por la ecuación de Planck: la observación de solo unos pocos valores de λ (o (u )) en el espectro lineal significaba que solo unos pocos valores de E eran posibles. Así los niveles de energía de un átomo de hidrógeno tuvieron que ser cuantificados ; en otras palabras, solo los estados que tenían ciertos valores de energía eran posibles, o permitido . Si un átomo de hidrógeno pudiera tener cualquier valor de energía, entonces se habría observado un espectro continuo, similar a la radiación del cuerpo negro.
En 1885, un profesor de matemáticas suizo, Johann Balmer (1825-1898), mostró que las frecuencias de las líneas observadas en la región visible del espectro de hidrógeno se ajustan a una ecuación simple que se puede expresar de la siguiente manera:
[u = constante ; left ( dfrac {1} {2 ^ {2}} – dfrac {1} {n ^ {^ {2}}} right) label {6.3.1} ]
donde n = 3, 4, 5, 6. Como resultado, estas líneas se conocen como la serie Balmer . El físico sueco Johannes Rydberg (1854–1919) posteriormente reformuló y amplió el resultado de Balmer en la ecuación de Rydberg :
[ dfrac {1} { lambda} = Re ; left ( dfrac {1} {n ^ {2} _ {1}} – dfrac {1} {n ^ {2} _ {2}} right) label {6.3.2} ] [19459012 ]
donde (n_1 ) y (n_2 ) son enteros positivos, (n_2> n_1 ) y ( Re ) la constante de Rydberg , tiene un valor de 1.09737 × 10 7 m −1 .
Al igual que la ecuación de Balmer, la ecuación simple de Rydberg describió las longitudes de onda de las líneas visibles en el espectro de emisión de hidrógeno (con n 1 = 2, n [ 19459017] 2 = 3, 4, 5, …). Más importante aún, la ecuación de Rydberg también predijo las longitudes de onda de otras series de líneas que se observarían en el espectro de emisión de hidrógeno: uno en el ultravioleta ( n 1 = 1, n 2 = 2, 3, 4, …) y uno en el infrarrojo ( n 1 = 3, n 2 = 4, 5, 6). Desafortunadamente, los científicos aún no habían desarrollado ninguna justificación teórica para una ecuación de esta forma.
Modelo de Bohr
En 1913, un físico danés, Niels Bohr (1885-1962; Premio Nobel de Física, 1922), propuso un modelo teórico para el átomo de hidrógeno que explicaba su espectro de emisión. El modelo de Bohr requería solo una suposición: El electrón se mueve alrededor del núcleo en órbitas circulares que solo pueden tener ciertos radios permitidos. El modelo anterior del átomo de Rutherford también había supuesto que los electrones se movían en órbitas circulares alrededor del núcleo y que el átomo se mantenía unido por la atracción electrostática entre el núcleo cargado positivamente y el electrón cargado negativamente. Aunque ahora sabemos que la suposición de órbitas circulares era incorrecta, la idea de Bohr fue proponer que el electrón podría ocupar solo ciertas regiones del espacio .
Utilizando la física clásica, Niels Bohr demostró que la energía de un electrón en una órbita particular está dada por
[E_ {n} = dfrac {- Re hc} {n ^ {2}} label {6.3.3} ]
donde ( Re ) es la constante de Rydberg, h es la constante de Planck, c es la velocidad de la luz, y n es un positivo entero correspondiente al número asignado a la órbita, con n = 1 correspondiente a la órbita más cercana al núcleo. En este modelo n = ∞ corresponde al nivel donde la energía que mantiene unidos el electrón y el núcleo es cero. En ese nivel, el electrón no está unido al núcleo y el átomo se ha separado en un ion cargado negativamente (el electrón) y un ion cargado positivamente (el núcleo). En este estado, el radio de la órbita también es infinito. El átomo ha sido ionizado.
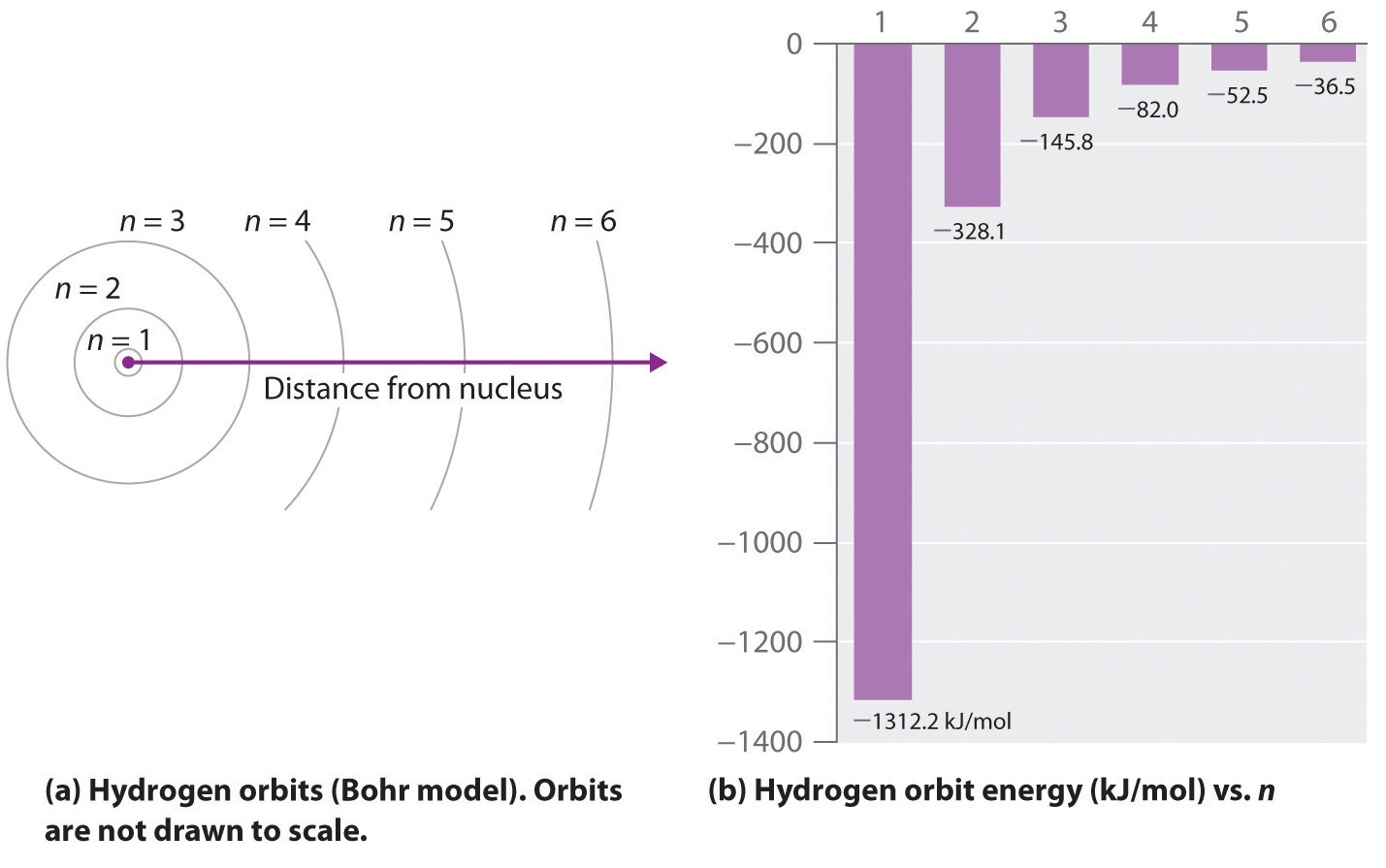
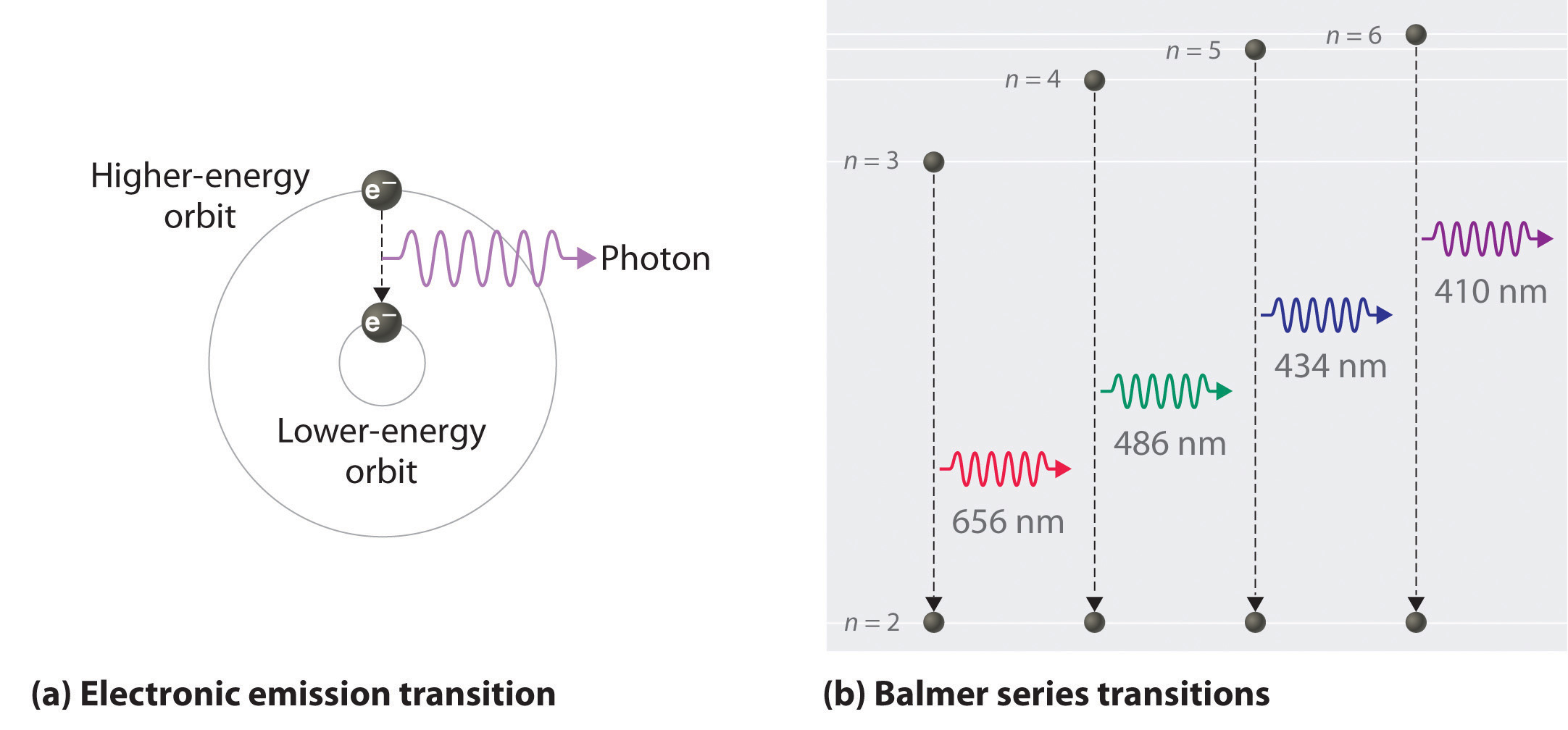
A medida que n disminuye, la energía que mantiene unidos el electrón y el núcleo se vuelve cada vez más negativa, el radio de la órbita se reduce y se necesita más energía para ionizar el átomo. La órbita con n = 1 es la mentira más baja y más estrechamente unida. El signo negativo en la ecuación ( ref {6.3.3} ) indica que el par electrón-núcleo está más unido (es decir, a una energía potencial más baja) cuando están cerca uno del otro que cuando están muy separados. Debido a que un átomo de hidrógeno con su único electrón en esta órbita tiene la energía más baja posible, este es el estado fundamental (la disposición más estable de electrones para un elemento o compuesto) para un átomo de hidrógeno. A medida que aumenta n, aumenta el radio de la órbita; el electrón está más alejado del protón, lo que resulta en una disposición menos estable con mayor energía potencial (Figura ( PageIndex {2a} )). Por lo tanto, un átomo de hidrógeno con un electrón en una órbita con n> 1 está en un estado excitado , definido como cualquier disposición de electrones que es más alta en energía que el estado fundamental. Cuando un átomo en un estado excitado experimenta una transición al estado fundamental en un proceso llamado desintegración, pierde energía al emitir un fotón cuya energía corresponde a la diferencia en energía entre los dos estados (Figura ( Índice de página {1} )).
Entonces, la diferencia en energía (Δ E ) entre dos órbitas o niveles de energía viene dada por ( Delta E = E_ {n_ {1}} – E_ {n_ {2}} ) donde n 1 es la órbita final y n 2 la órbita inicial. Sustituyendo la ecuación de Bohr (Ecuación 6.3.3) por cada valor de energía se obtiene
[ Delta E = E_ {final} -E_ {initial} = – dfrac { Re hc} {n_ {2} ^ {2}} – left (- dfrac { Re hc} { n_ {1} ^ {2}} right) = – Re hc left ( dfrac {1} {n_ {2} ^ {2}} – dfrac {1} {n_ {1} ^ {2} } right) label {6.3.4} ]
Si n 2 > n 1 , la transición es de un estado de mayor energía (órbita de radio más grande) a un estado de energía inferior (órbita de radio más pequeño), como se muestra con la flecha punteada en la parte (a) en la Figura ( PageIndex {3} ). Sustituyendo hc / λ por Δ E da
[ Delta E = dfrac {hc} { lambda} = – Re hc left ( dfrac {1} {n_ {2} ^ {2}} – dfrac {1} {n_ { 1} ^ {2}} right) label {6.3.5} ]
Cancelando hc en ambos lados da
[ dfrac {1} { lambda} = – Re left ( dfrac {1} {n_ {2} ^ {2}} – dfrac {1} {n_ {1} ^ {2 }} right) label {6.3.6} ]
Excepto por el signo negativo, esta es la misma ecuación que Rydberg obtuvo experimentalmente. El signo negativo en las ecuaciones ( ref {6.3.5} ) y ( ref {6.3.6} ) indica que la energía se libera a medida que el electrón se mueve desde la órbita n 2 en órbita n 1 porque la órbita n 2 está a una energía más alta que la órbita n [ 19459017] 1 . Bohr calculó el valor de ( Re ) a partir de constantes fundamentales como la carga y la masa del electrón y la constante de Planck y obtuvo un valor de 1.0974 × 10 7 m −1 , el mismo número que Rydberg había obtenido al analizar los espectros de emisión.
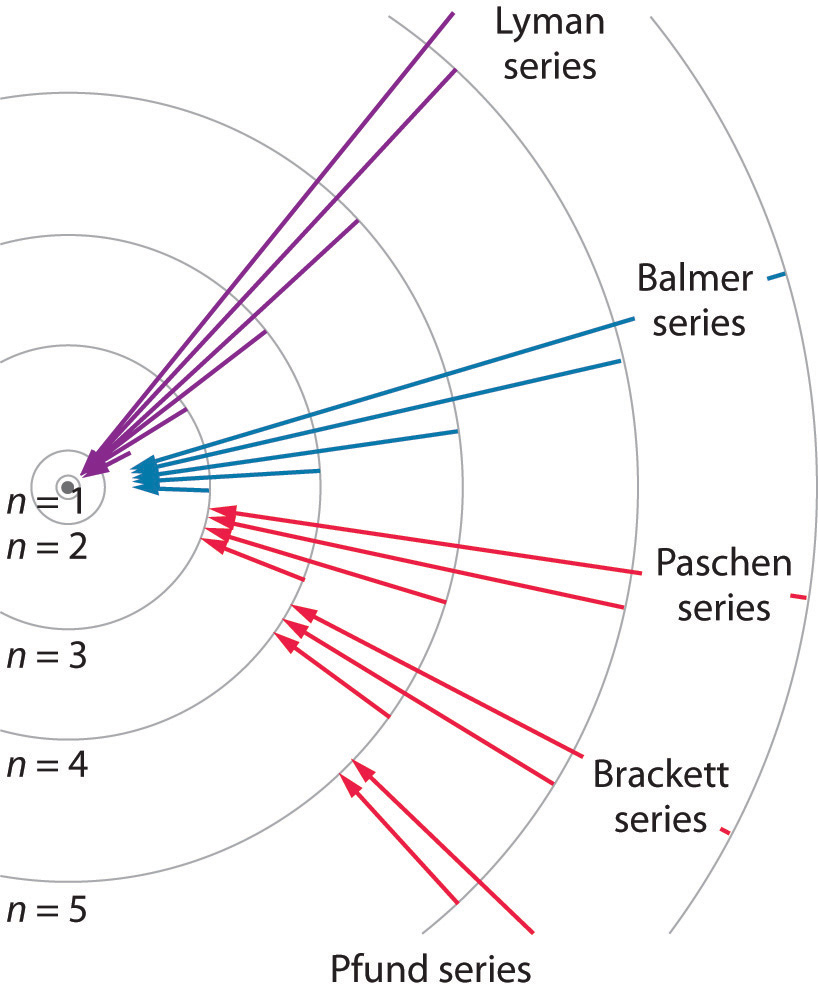
Ahora podemos entender la base física de la serie de líneas Balmer en el espectro de emisión de hidrógeno ( ( PageIndex {3b} )); Las líneas de esta serie corresponden a transiciones de órbitas de mayor energía (n> 2) a la segunda órbita (n = 2). Por lo tanto, los átomos de hidrógeno en la muestra han absorbido energía de la descarga eléctrica y decaído de un estado excitado de mayor energía (n> 2) a un estado de menor energía (n = 2) emitiendo un fotón de radiación electromagnética cuya energía corresponde exactamente a la diferencia de energía entre los dos estados (Figura ( PageIndex {3a} )). La transición n = 3 a n = 2 da lugar a la línea a 656 nm (rojo), la transición n = 4 a n = 2 a la línea a 486 nm (verde), la transición n = 5 a n = 2 a la línea a 434 nm (azul) y la transición n = 6 a n = 2 a la línea a 410 nm (violeta). Debido a que una muestra de hidrógeno contiene una gran cantidad de átomos, la intensidad de las diversas líneas en un espectro lineal depende de la cantidad de átomos en cada estado excitado. A la temperatura en el tubo de descarga de gas, hay más átomos en los niveles n = 3 que n ≥ 4. En consecuencia, la transición n = 3 a n = 2 es la línea más intensa, que produce el color rojo característico de una descarga de hidrógeno (Figura ( PageIndex {1a} )). Otras familias de líneas son producidas por transiciones desde estados excitados con n> 1 a la órbita con n = 1 o hacia órbitas con n ≥ 3. Estas transiciones se muestran esquemáticamente en la Figura ( PageIndex {4} )
El modelo de Bohr del átomo de hidrógeno dio una explicación exacta de su espectro de emisión observado. Las siguientes son sus contribuciones clave a nuestra comprensión de la estructura atómica:
- Los electrones pueden ocupar solo ciertas regiones del espacio, llamadas órbitas .
- Las órbitas más cercanas al núcleo tienen menos energía.
- Los electrones pueden moverse de una órbita a otra absorbiendo o emitiendo energía, dando lugar a espectros característicos.
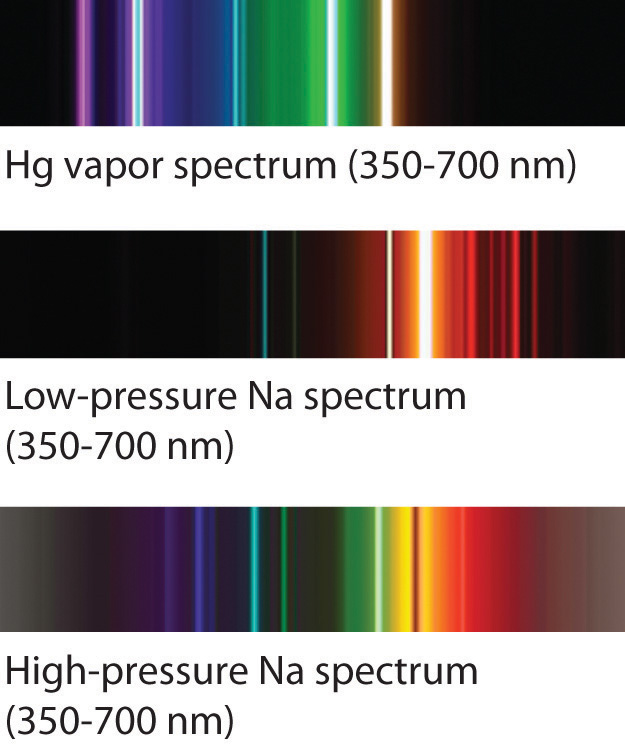
Desafortunadamente, Bohr no pudo explicar por qué el electrón debería restringirse a órbitas particulares. Además, a pesar de una gran cantidad de ajustes, como suponer que las órbitas podrían ser elipses en lugar de círculos, su modelo no podía explicar cuantitativamente los espectros de emisión de ningún elemento que no sea hidrógeno (Figura ( PageIndex {5} )). De hecho, el modelo de Bohr funcionó solo para especies que contenían un solo electrón: H, He + , Li 2 + , y así sucesivamente. Los científicos necesitaban un cambio fundamental en su forma de pensar acerca de la estructura electrónica de los átomos para avanzar más allá del modelo de Bohr.



Figura ( PageIndex {5} ): El espectro de emisión de elementos comparados con hidrógeno. Estas imágenes muestran (a) gas hidrógeno, que se atomiza a átomos de hidrógeno en el tubo de descarga; (b) neón; y (c) mercurio. Las líneas más fuertes en el espectro de hidrógeno están en la serie lejana UV Lyman que comienza a 124 nm y menos. Las líneas más fuertes en el espectro de mercurio están a 181 y 254 nm, también en UV. Estos no se muestran.
Los estados de energía del átomo de hidrógeno
Hasta ahora hemos considerado explícitamente solo la emisión de luz por los átomos en estados excitados, lo que produce un espectro de emisión (un espectro producido por la emisión de luz por los átomos en estados excitados). A la inversa, la absorción de la luz por los átomos del estado fundamental para producir un estado excitado, también puede ocurrir, produciendo un espectro de absorción (un espectro producido por la absorción de luz por los átomos del estado fundamental).
Si se pasa luz blanca a través de una muestra de hidrógeno, los átomos de hidrógeno absorben energía a medida que un electrón se excita a niveles de energía más altos (orbita con n ≥ 2). Si la luz que emerge pasa a través de un prisma, forma un espectro continuo con líneas negras (correspondientes a que no pasa luz a través de la muestra) a 656, 468, 434 y 410 nm. Estas longitudes de onda corresponden a n = 2 a n = 3, n = 2 a n = 4, n [ 19459011] = 2 a n = 5, y n = 2 a n = 6 transiciones. Por lo tanto, cualquier elemento dado tiene tanto un espectro de emisión característico como un espectro de absorción característico, que son esencialmente imágenes complementarias.
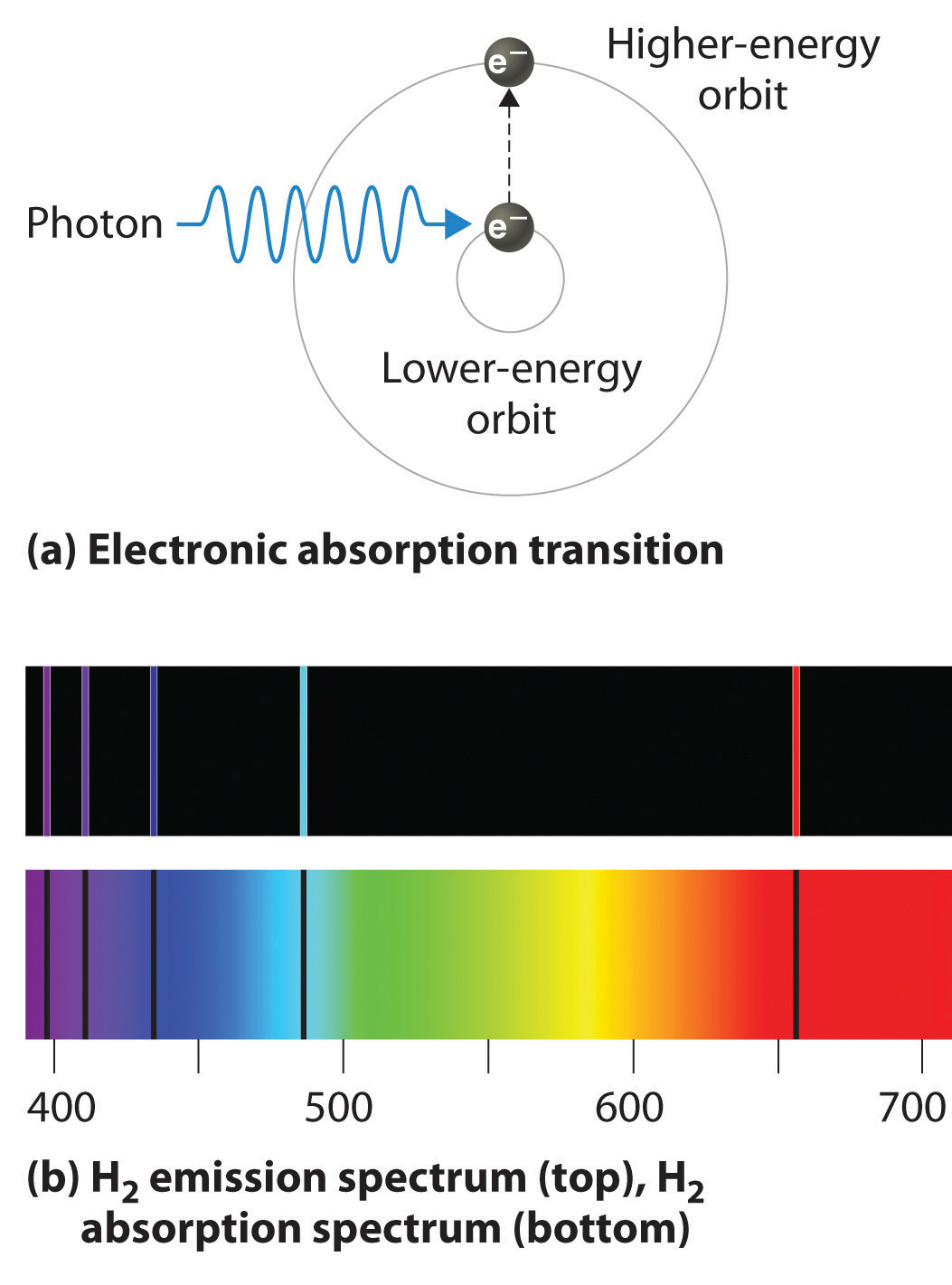
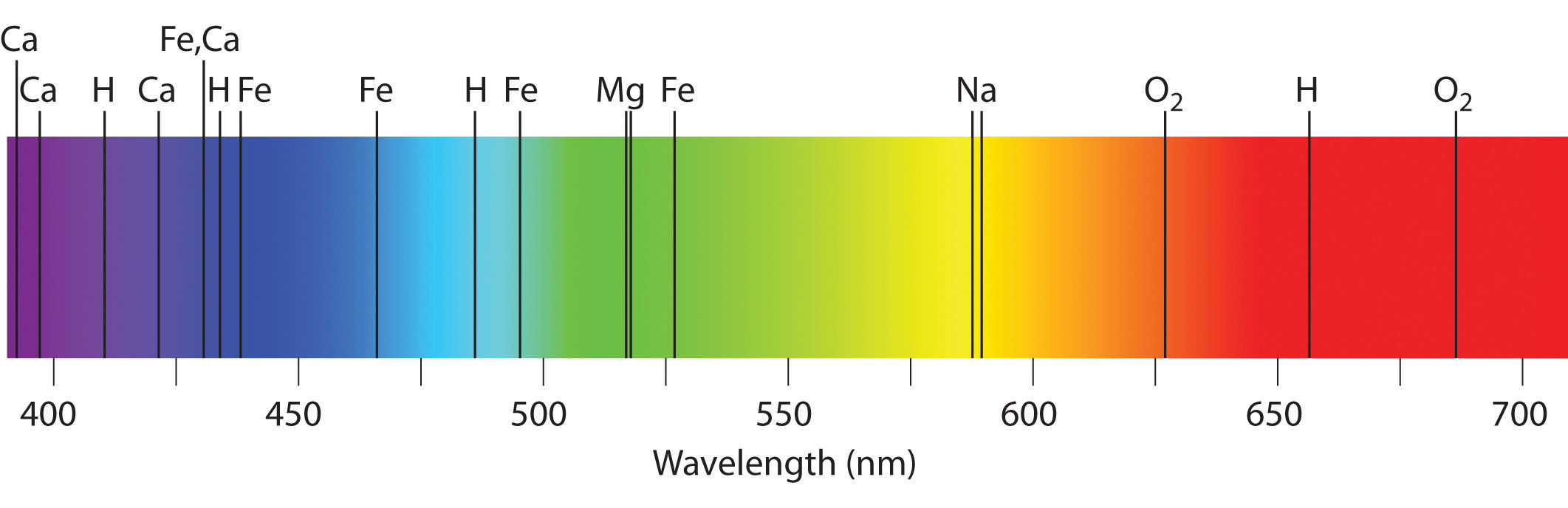
Los espectros de emisión y absorción forman la base de la espectroscopía , que utiliza espectros para proporcionar información sobre la estructura y la composición de una sustancia u objeto. En particular, los astrónomos utilizan los espectros de emisión y absorción para determinar la composición de las estrellas y la materia interestelar. Como ejemplo, considere el espectro de la luz solar que se muestra en la Figura ( PageIndex {7} ) Debido a que el sol está muy caliente, la luz que emite tiene la forma de un espectro de emisión continua. Sin embargo, se superpone a ella una serie de líneas oscuras debido principalmente a la absorción de frecuencias específicas de luz por átomos más fríos en la atmósfera exterior del sol. Al comparar estas líneas con los espectros de elementos medidos en la Tierra, ahora sabemos que el sol contiene grandes cantidades de hidrógeno, hierro y carbono, junto con pequeñas cantidades de otros elementos. Durante el eclipse solar de 1868, el astrónomo francés Pierre Janssen (1824–1907) observó un conjunto de líneas que no coincidían con las de ningún elemento conocido. Sugirió que se debían a la presencia de un nuevo elemento, al que llamó helio , del griego helios , que significa “sol”. El helio fue finalmente descubierto en minerales de uranio en la Tierra en 1895. Las partículas alfa son núcleos de helio. Las partículas alfa emitidas por el uranio radiactivo recogen electrones de las rocas para formar átomos de helio.
El color rojo familiar de los letreros de neón utilizados en publicidad se debe al espectro de emisión de neón que se muestra en la parte (b) en la Figura ( PageIndex {5} ). Del mismo modo, los colores azul y amarillo de ciertas farolas son causados, respectivamente, por descargas de mercurio y sodio. En todos estos casos, una descarga eléctrica excita los átomos neutros a un estado de mayor energía, y la luz se emite cuando los átomos decaen al estado fundamental. En el caso del mercurio, la mayoría de las líneas de emisión están por debajo de 450 nm, lo que produce una luz azul (parte (c) en la Figura ( PageIndex {5} )). En el caso del sodio, las líneas de emisión más intensas están a 589 nm, lo que produce una luz amarilla intensa.
Resumen
Existe una conexión íntima entre la estructura atómica de un átomo y sus características espectrales. Los átomos de elementos individuales emiten luz solo a longitudes de onda específicas, produciendo un espectro lineal en lugar del espectro continuo de todas las longitudes de onda producidas por un objeto caliente. Niels Bohr explicó el espectro lineal del átomo de hidrógeno al suponer que el electrón se movía en órbitas circulares y que solo se permitían órbitas con ciertos radios determinados. Las líneas en el espectro se debieron a transiciones en las que un electrón se movió desde una órbita de mayor energía con un radio más grande a una órbita de menor energía con un radio más pequeño. La órbita más cercana al núcleo representaba el estado fundamental del átomo y era más estable; Las órbitas más alejadas eran estados excitados de mayor energía . Las transiciones de un estado excitado a un estado de menor energía dieron como resultado la emisión de luz con solo un número limitado de longitudes de onda. Los átomos también pueden absorber la luz de ciertas energías, lo que resulta en una transición desde el estado fundamental o un estado excitado de menor energía a un estado excitado de mayor energía. Esto produce un espectro de absorción , que tiene líneas oscuras en la misma posición que las líneas brillantes en el espectro de emisión de un elemento. El modelo de Bohr revolucionó la comprensión del átomo, pero no pudo explicar el espectro de átomos más pesados que el hidrógeno.
Colaboradores
-
Modificado por Joshua Halpern ( Universidad de Howard )