Los fotones de luz de Einstein eran paquetes individuales de energía que tenían muchas de las características de las partículas. Recuerde que la colisión de un electrón (una partícula) con un fotón suficientemente energético puede expulsar un fotoelectrón de la superficie de un metal. Cualquier exceso de energía se transfiere al electrón y se convierte en la energía cinética del electrón expulsado. La hipótesis de Einstein de que la energía se concentra en paquetes localizados, sin embargo, contrasta fuertemente con la noción clásica de que la energía se distribuye uniformemente en una ola. Ahora describimos la teoría de Einstein sobre la relación entre energía y masa, una teoría que otros construyeron para desarrollar nuestro modelo actual del átomo.
El carácter ondulatorio de la materia
Einstein inicialmente asumió que los fotones tenían masa cero, lo que los convirtió en un tipo peculiar de partículas. En 1905, sin embargo, publicó su teoría especial de la relatividad, que relacionaba la energía y la masa de acuerdo con la famosa ecuación:
[E = h
u = h dfrac {c} { lambda} = mc ^ {2} label {6.4.1} ]
Según esta teoría, un fotón de longitud de onda (λ ) y frecuencia (
u ) tiene una masa distinta de cero, que se da de la siguiente manera:
[m = dfrac {E} {c ^ {2}} = dfrac {h
u} {c ^ {2}} = dfrac {h} { lambda c} label {6.4.2} ]
Es decir, la luz, que siempre se había considerado una onda, también tiene propiedades típicas de las partículas, una condición conocida como dualidad onda-partícula (un principio de que la materia y la energía tienen propiedades típicas de las ondas y las partículas). Dependiendo de las condiciones, la luz podría verse como una onda o una partícula.
En 1922, el físico estadounidense Arthur Compton (1892-1962) informó los resultados de los experimentos que involucraron la colisión de rayos X y electrones que respaldaron la naturaleza de las partículas de la luz. Casi al mismo tiempo, un joven estudiante francés de física, Louis de Broglie (1892–1972), comenzó a preguntarse si lo contrario era cierto: ¿podrían las partículas exhibir las propiedades de las ondas? En su tesis doctoral presentada a la Sorbona en 1924, de Broglie propuso que una partícula como un electrón podría describirse por una onda cuya longitud de onda está dada por
[ lambda = dfrac {h} {mv} label {6.4.3} ]
donde
- (h ) es la constante de Planck,
- (m ) es la masa de la partícula y
- (v ) es la velocidad de la partícula.
Esta idea revolucionaria fue confirmada rápidamente por los físicos estadounidenses Clinton Davisson (1881–1958) y Lester Germer (1896–1971), quienes mostraron que haces de electrones, considerados partículas, fueron difractados por un cristal de cloruro de sodio de la misma manera como rayos X, que se consideraban ondas. Se probó experimentalmente que los electrones exhiben las propiedades de las ondas. Por su trabajo, de Broglie recibió el Premio Nobel de Física en 1929.
Si las partículas exhiben las propiedades de las ondas, ¿por qué nadie las había observado antes? La respuesta se encuentra en el numerador de la ecuación de De Broglie, que es un número extremadamente pequeño. Como calculará en el Ejemplo ( PageIndex {1} ), la constante de Planck (6.63 × 10 −34 J • s) es tan pequeña que la longitud de onda de una partícula con una masa grande es demasiado corta (menor que el diámetro de un núcleo atómico) para ser notable.
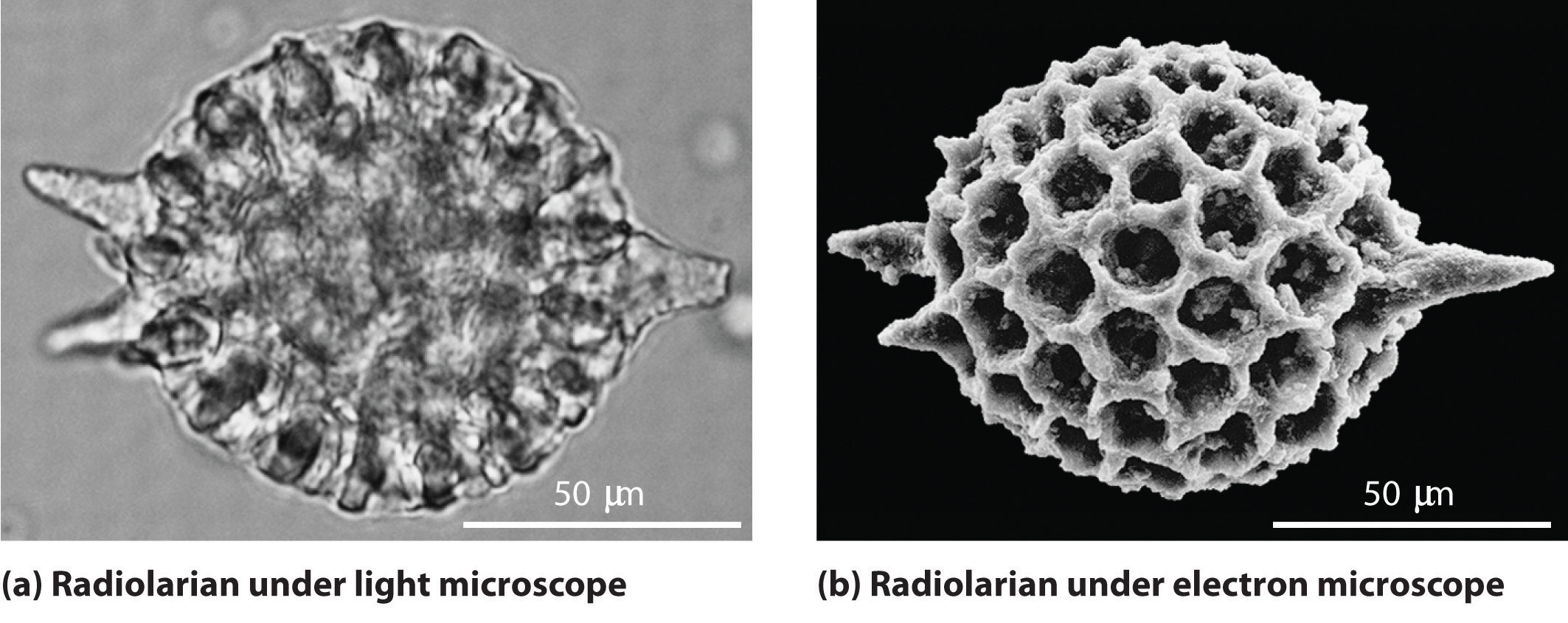
Como calculó en el Ejemplo ( PageIndex {1} ), los objetos como una pelota de béisbol o un neutrón tienen longitudes de onda tan cortas que se consideran mejor principalmente como partículas. Por el contrario, los objetos con masas muy pequeñas (como los fotones) tienen longitudes de onda grandes y pueden verse principalmente como ondas. Sin embargo, los objetos con masas intermedias, como los electrones, exhiben las propiedades de ambas partículas y ondas. Aunque todavía solemos pensar en los electrones como partículas, la naturaleza ondulatoria de los electrones se emplea en un microscopio electrónico , que ha revelado la mayor parte de lo que sabemos sobre la estructura microscópica de los organismos y materiales vivos. Debido a que la longitud de onda de un haz de electrones es mucho más corta que la longitud de onda de un haz de luz visible, este instrumento puede resolver detalles más pequeños que un microscopio de luz (Figura ( PageIndex {1} )).
Ondas estacionarias
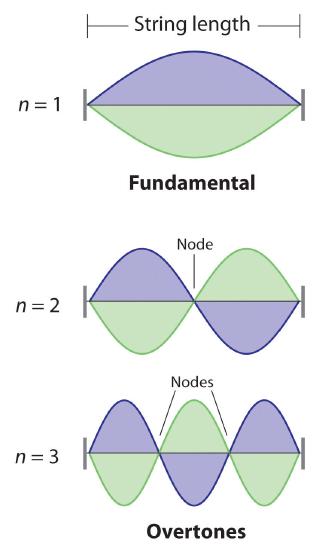
De Broglie también investigó por qué solo ciertas órbitas estaban permitidas en el modelo de átomo de hidrógeno de Bohr. Supuso que el electrón se comporta como una onda estacionaria (una onda que no viaja en el espacio). Un ejemplo de una onda estacionaria es el movimiento de una cuerda de violín o guitarra. Cuando se arranca la cuerda, vibra a ciertas frecuencias fijas porque está sujeta en ambos extremos (Figura ( PageIndex {3} )). Si la longitud de la cuerda es (L ), entonces la vibración de energía más baja (la fundamental) tiene longitud de onda
[ begin {align} dfrac { lambda} {2} & = L
onumber \ lambda & = 2L
onumber end {align} label {6.4.4} ]
Las vibraciones de mayor energía se denominan armónicos (la vibración de una onda estacionaria que es más alta en energía que la vibración fundamental) y se producen cuando la cuerda se toca con más fuerza; tienen longitudes de onda dadas por
[ lambda = dfrac {2L} {n} label {6.4.5} ]
donde n tiene cualquier valor integral. Cuando se arranca, todas las demás frecuencias se extinguen inmediatamente. Solo las frecuencias resonantes sobreviven y se escuchan. Por lo tanto, podemos pensar en las frecuencias resonantes de la cuerda como cuantificadas. Observe en la Figura ( PageIndex {3} ) que todos los armónicos tienen uno o más nodos, puntos donde la cadena no se mueve. La amplitud de la onda en un nodo es cero.
Las vibraciones cuantificadas y los sobretonos que contienen nodos no están restringidos a sistemas unidimensionales, como las cadenas. Una superficie bidimensional, como un parche, también tiene vibraciones cuantizadas. De manera similar, cuando los extremos de una cuerda se unen para formar un círculo, las únicas vibraciones permitidas son aquellas con longitud de onda
[2πr = nλ label {6.4.6} ]
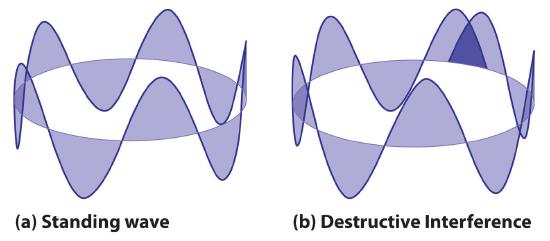
donde (r ) es el radio del círculo. De Broglie argumentó que las órbitas permitidas de Bohr podrían entenderse si el electrón se comportara como una onda circular (Figura ( PageIndex {4} )). La onda estacionaria podría existir solo si la circunferencia del círculo fuera un múltiplo integral de la longitud de onda de tal manera que las ondas propagadas estuvieran todas en fase, aumentando así las amplitudes netas y causando interferencia constructiva . De lo contrario, las ondas propagadas estarían desfasadas, lo que resultaría en una disminución neta de la amplitud y causaría interferencia destructiva. ¡Las ondas no resonantes interfieren entre sí! La idea de De Broglie explicaba muy bien las órbitas permitidas y los niveles de energía de Bohr: en el nivel de energía más bajo, correspondiente a (n = 1 ) en la Ecuación ( ref {6.4.6} ), una longitud de onda completa cerraría el círculo. Los niveles de energía más altos tendrían valores sucesivamente más altos de n con un número correspondiente de nodos.
Como todas las analogías, aunque el modelo de onda estacionaria nos ayuda a comprender mucho sobre por qué funcionó la teoría de Bohr, también, si se empuja demasiado, puede inducir a error. Como verá, algunas de las ideas de De Broglie se retienen en la teoría moderna de la estructura electrónica del átomo: el comportamiento ondulatorio del electrón y la presencia de nodos que aumentan en número a medida que aumenta el nivel de energía. Desafortunadamente, su explicación (y la de Bohr) también contiene una característica importante que ahora sabemos que es incorrecta: en el modelo actualmente aceptado, el electrón en una órbita dada está no siempre a la misma distancia del núcleo.
El principio de incertidumbre de Heisenberg
Debido a que una onda es una perturbación que viaja en el espacio, no tiene una posición fija. Por lo tanto, uno podría esperar que también sería difícil especificar la posición exacta de una partícula que exhibe un comportamiento ondulatorio. Una característica de la luz es que puede doblarse o extenderse al pasar a través de una ranura estrecha. Literalmente puede ver esto cerrando los ojos a la mitad y mirando a través de las pestañas. Esto reduce el brillo de lo que está viendo y borra un poco la imagen, pero la luz se dobla alrededor de las pestañas para proporcionar una imagen completa en lugar de un montón de barras en la imagen. Esto se llama difracción.
Este comportamiento de las ondas se captura en las ecuaciones de Maxwell (1870 más o menos) para ondas electromagnéticas y fue y es bien entendido. Un “principio de incertidumbre” para la luz es, por así decirlo, simplemente una conclusión sobre la naturaleza de las ondas electromagnéticas y nada nuevo. La idea de De Broglie de la dualidad onda-partícula significa que las partículas como los electrones que exhiben características ondulatorias también sufrirán difracción de las rendijas cuyo tamaño es del orden de la longitud de onda del electrón.
Esta situación fue descrita matemáticamente por el físico alemán Werner Heisenberg (1901-1976; Premio Nobel de Física, 1932), quien relacionó la posición de una partícula con su impulso. Refiriéndose al electrón, Heisenberg declaró que “en cada momento el electrón tiene solo una posición inexacta y una velocidad inexacta, y entre estas dos inexactitudes existe esta relación de incertidumbre”. Matemáticamente, el principio de incertidumbre de Heisenberg establece que la incertidumbre en la posición de una partícula (Δ x ) multiplicada por la incertidumbre en su el momento [Δ ( mv )] es mayor o igual que la constante de Planck dividida por 4π:
[ left ( Delta x right) left ( Delta left [mv right] right) ge dfrac {h} {4 pi} label {6.4.7} ]
Debido a que la constante de Planck es un número muy pequeño, el principio de incertidumbre de Heisenberg es importante solo para partículas como los electrones que tienen masas muy bajas. Estas son las mismas partículas predichas por la ecuación de De Broglie para tener longitudes de onda medibles.
Si la posición precisa (x ) de una partícula se conoce absolutamente (Δ x = 0), entonces la incertidumbre en su momento debe ser infinita:
[ left ( Delta left [mv right] right) = dfrac {h} {4 pi left ( Delta x right)} = dfrac {h} {4 pi left (0 right)} = infty label {6.4.8} ]
Debido a que la masa del electrón en reposo ( (m )) es constante y precisa, la incertidumbre en (Δ (mv) ) debe deberse al término (Δv ), que sería tiene que ser infinitamente grande para que (Δ (mv) ) sea igual al infinito. Es decir, de acuerdo con la Ecuación ( ref {6.4.8} ), cuanto más exactamente sepamos la posición exacta del electrón (como (Δx → 0 )), menos exactamente conoceremos la velocidad y la cinética energía del electrón (1/2 mv 2 ) porque (Δ (mv) → ∞ ). Por el contrario, cuanto más exactamente sepamos el momento preciso (y la energía) del electrón [como (Δ (mv) → 0 )], entonces (Δx → ∞ ) y no tenemos idea de dónde está el electrón.
El modelo de Bohr del átomo de hidrógeno violó el principio de incertidumbre de Heisenberg al tratar de especificar simultáneamente tanto la posición (una órbita de un radio particular) como la energía (una cantidad relacionada con el momento) del electrón . Además, dada su naturaleza de masa y onda, el electrón en el átomo de hidrógeno no podría orbitar el núcleo en un camino circular bien definido como lo predice Bohr. Sin embargo, verá que el radio más probable del electrón en el átomo de hidrógeno es exactamente el predicho por el modelo de Bohr.
Resumen
Un electrón posee propiedades de partículas y ondas. El modelo moderno para la estructura electrónica del átomo se basa en reconocer que un electrón posee propiedades de partículas y ondas, la llamada dualidad onda-partícula . Louis de Broglie demostró que la longitud de onda de una partícula es igual a la constante de Planck dividida por la masa multiplicada por la velocidad de la partícula.
[ lambda = dfrac {h} {mv}
onumber ]
El electrón en las órbitas circulares de Bohr podría describirse como una onda estacionaria , una que no se mueve a través del espacio. Las ondas estacionarias son familiares en la música: la onda estacionaria de energía más baja es la vibración fundamental , y las vibraciones de energía más alta son armónicos y tienen sucesivamente más nodos , puntos donde la amplitud de la onda es siempre cero. El principio de incertidumbre de Werner Heisenberg establece que es imposible describir con precisión tanto la ubicación como la velocidad de las partículas que exhiben un comportamiento ondulatorio.
[ left ( Delta x right) left ( Delta left [mv right] right) geqslant dfrac {h} {4 pi}
onumber ]
Colaboradores
-
Modificado por Joshua Halpern ( Universidad de Howard )