Un orbital es el refinamiento mecánico cuántico de la órbita de Bohr. En contraste con su concepto de una órbita circular simple con un radio fijo, los orbitales son regiones del espacio derivadas matemáticamente con diferentes probabilidades de contener un electrón.
Una forma de representar las distribuciones de probabilidad de electrones se ilustró anteriormente para el orbital 1 s de hidrógeno. Como Ψ 2 da la probabilidad de encontrar un electrón en un volumen de espacio dado (como un picómetro cúbico), una gráfica de Ψ 2 versus la distancia desde el núcleo ( r ) es un gráfico de la densidad de probabilidad . El orbital 1 s es esféricamente simétrico, por lo que la probabilidad de encontrar un electrón 1 s en cualquier punto depende solo de su distancia desde el núcleo. La densidad de probabilidad es mayor en r = 0 (en el núcleo) y disminuye de manera constante al aumentar la distancia. A valores muy grandes de r , la densidad de probabilidad de electrones es muy pequeña pero no cero.
En contraste, podemos calcular la probabilidad radial (la probabilidad de encontrar un electrón 1 s a una distancia r del núcleo) sumando las probabilidades de que un electrón esté en todos los puntos en una serie de x capas esféricas de radio r 1 , r 2 , r 3 ,…, r x – 1 , r x . En efecto, estamos dividiendo el átomo en capas concéntricas muy delgadas, muy parecidas a las capas de una cebolla (Figura ( PageIndex {1a} )), y calculando la probabilidad de encontrar un electrón en cada capa esférica. Recuerde que la densidad de probabilidad de electrones es mayor en r = 0 (Figura ( PageIndex {1b} )), por lo que la densidad de puntos es mayor para las capas esféricas más pequeñas en la parte (a) de la Figura ( PageIndex {1} ). En contraste, el área de superficie de cada capa esférica es igual a 4π r 2 , que aumenta muy rápidamente al aumentar r (Figura ( PageIndex {1c } )). Debido a que el área superficial de las capas esféricas aumenta más rápidamente al aumentar r que la densidad de probabilidad de electrones disminuye, la gráfica de probabilidad radial tiene un máximo a una distancia particular (Figura ( PageIndex {1d} ) ) Lo más importante, cuando r es muy pequeño, el área de superficie de un caparazón esférico es tan pequeña que la probabilidad de encontrar un electrón cerca del núcleo es muy baja; en el núcleo, la probabilidad de electrones se desvanece (Figura ( PageIndex {1d} )).
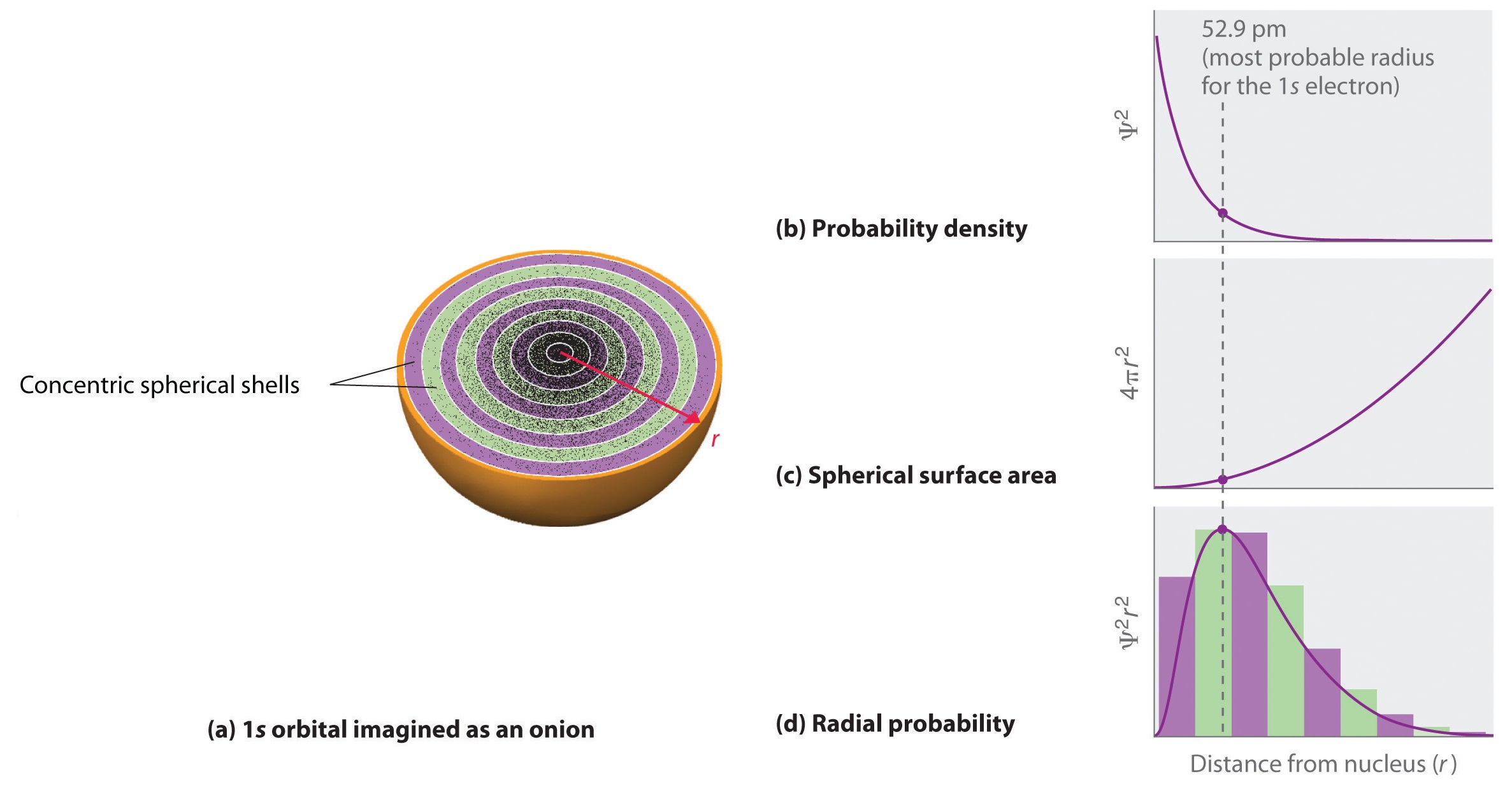
Para el átomo de hidrógeno, el pico en la gráfica de probabilidad radial ocurre en r = 0.529 Å (52.9 pm), que es exactamente el radio calculado por Bohr para el n = 1 órbita Así, el radio más probable obtenido de la mecánica cuántica es idéntico al radio calculado por la mecánica clásica. Sin embargo, en el modelo de Bohr, se suponía que el electrón estaba a esta distancia el 100% del tiempo, mientras que en el modelo de Schrödinger, está a esta distancia solo algunas veces. La diferencia entre los dos modelos es atribuible al comportamiento ondulatorio del electrón y al principio de incertidumbre de Heisenberg.
La figura ( PageIndex {2} ) compara las densidades de probabilidad de electrones para los orbitales 1 s , 2 s y 3 s . Tenga en cuenta que los tres son esféricamente simétricos. Sin embargo, para los orbitales 2 s y 3 s (y para todos los demás orbitales s ), la densidad de probabilidad de electrones no disminuye suavemente al aumentar r . En cambio, se observa una serie de mínimos y máximos en las gráficas de probabilidad radial (Figura ( PageIndex {2c} )). Los mínimos corresponden a nodos esféricos (regiones de probabilidad de electrones cero), que se alternan con regiones esféricas de probabilidad de electrones distinta de cero. La existencia de estos nodos es una consecuencia de los cambios de onda fase en la función de onda Ψ.

s Orbitales (l = 0)
Tres cosas suceden a s orbitales a medida que n aumenta (Figura ( PageIndex {2} )):
- Se hacen más grandes y se extienden más lejos del núcleo.
- Contienen más nodos. Esto es similar a una onda estacionaria que tiene regiones de amplitud significativa separadas por nodos, puntos con amplitud cero.
- Para un átomo dado, los orbitales s también se vuelven más altos en energía a medida que n aumenta debido a su mayor distancia del núcleo.
Los orbitales se dibujan generalmente como superficies tridimensionales que encierran el 90% de la densidad de electrones , como se mostró para el hidrógeno 1 s , 2 s y 3 orbitales s en la parte (b) en la Figura ( PageIndex {2} ). Aunque estos dibujos muestran los tamaños relativos de los orbitales, normalmente no muestran los nodos esféricos en los orbitales 2 s y 3 s porque los nodos esféricos se encuentran dentro de la superficie del 90%. Afortunadamente, las posiciones de los nodos esféricos no son importantes para la unión química.
p Orbitales (l = 1)
Solo los orbitales s son esféricamente simétricos. A medida que aumenta el valor de l , aumenta el número de orbitales en un subshell dado, y las formas de los orbitales se vuelven más complejas. Debido a que la subcapa 2 p tiene l = 1, con tres valores de m l (−1, 0 y +1), hay tres orbitales 2 p .
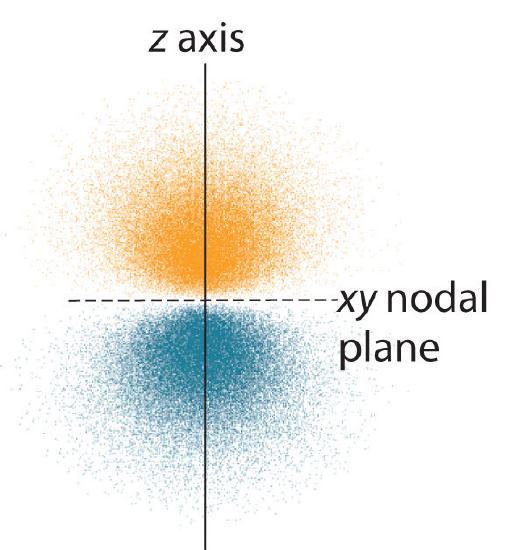
La distribución de probabilidad de electrones para uno de los orbitales de hidrógeno 2 p se muestra en la Figura ( PageIndex {3} ). Debido a que este orbital tiene dos lóbulos de densidad electrónica dispuestos a lo largo del eje z , con una densidad electrónica de cero en el plano xy (es decir, el plano xy es un plano nodal), es un orbital (2p_z ). Como se muestra en la Figura ( PageIndex {4} ), los otros dos orbitales 2 p tienen formas idénticas, pero se encuentran a lo largo del eje x ( (2p_x )) y eje y ( (2p_y )), respectivamente. Tenga en cuenta que cada p orbital tiene solo un plano nodal . En cada caso, la fase de la función de onda para cada uno de los 2 orbitales p es positiva para el lóbulo que apunta a lo largo del eje positivo y negativa para el lóbulo que apunta a lo largo del eje negativo. Es importante enfatizar que estos signos corresponden a la fase de la onda que describe el movimiento del electrón, no a cargas positivas o negativas.
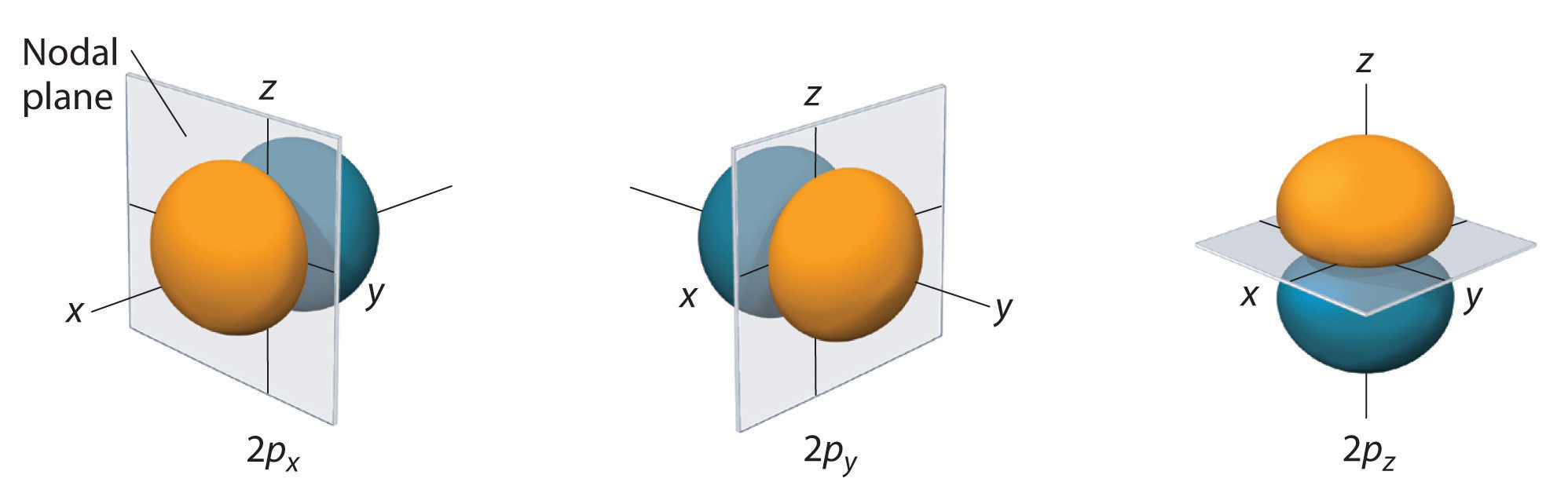
Las superficies que se muestran encierran el 90% de la probabilidad total de electrones para el 2 p x , 2 p [ 19459010] y , y 2 p z orbitales. Cada orbital está orientado a lo largo del eje indicado por el subíndice y un plano nodal que es perpendicular a ese eje biseca cada orbital 2 p . La fase de la función de onda es positiva (naranja) en la región del espacio donde x , y o z es positiva y negativa (azul) donde [ 19459010] x , y o z es negativo. Al igual que con los orbitales s , el tamaño y la complejidad de los orbitales p para cualquier átomo aumentan a medida que aumenta el número cuántico principal n . Las formas de las superficies de probabilidad del 90% de los orbitales 3 p , 4 p y de mayor energía p son, sin embargo, esencialmente las mismas que se muestran en la Figura ( PageIndex {4} ).
d Orbitales (l = 2)
Las subcapas con l = 2 tienen cinco orbitales d ; el primer caparazón principal que tiene una d subshell corresponde a n = 3. Los cinco d orbitales tienen m [19459010 ] l valores de −2, −1, 0, +1 y +2.
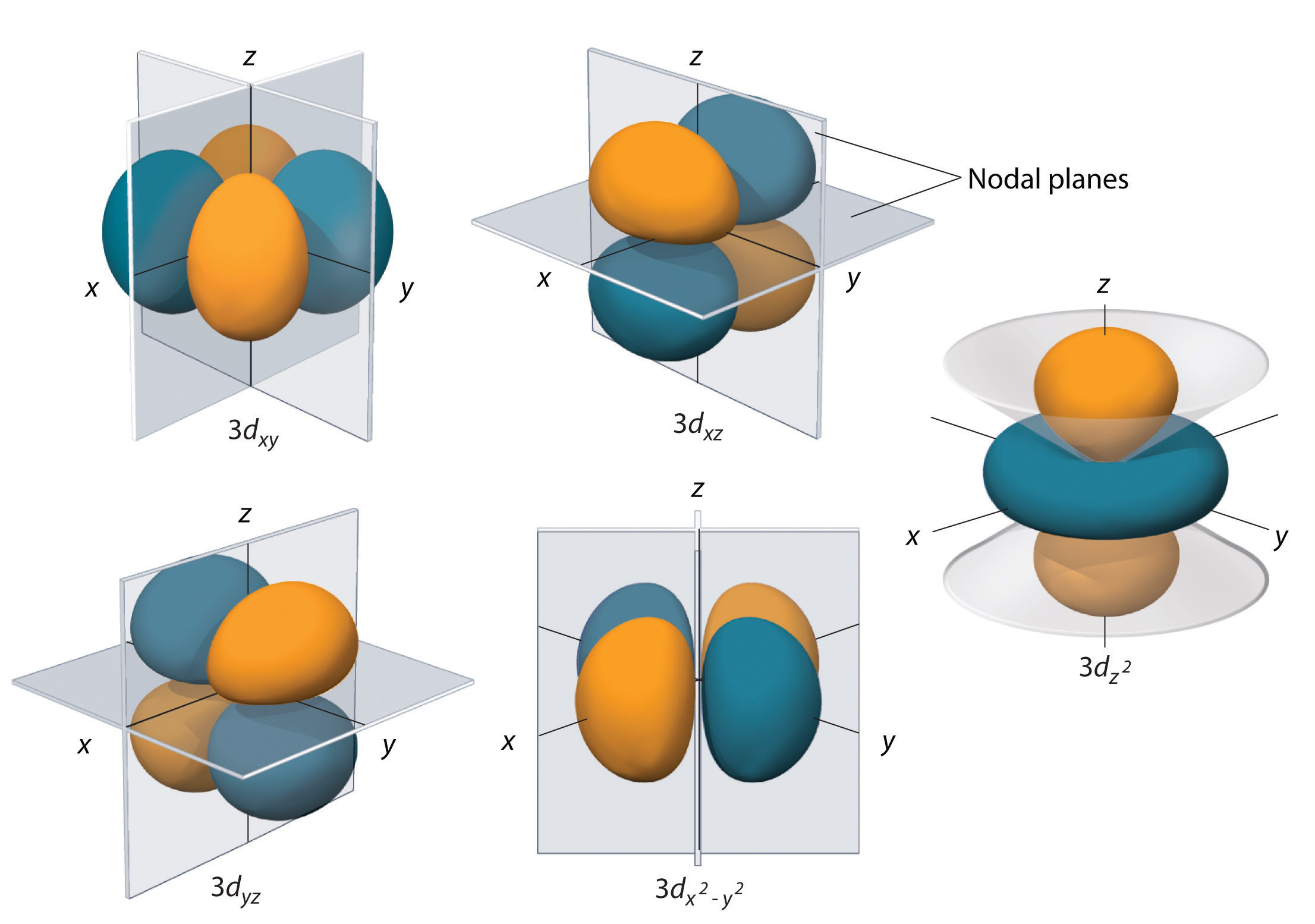
Los orbitales 3d de hidrógeno, que se muestran en la Figura ( PageIndex {5} ), tienen formas más complejas que los orbitales 2p. Los cinco orbitales 3d contienen dos superficies nodales, en comparación con una para cada orbital p y cero para cada orbital s. En tres de los orbitales d, los lóbulos de densidad electrónica están orientados entre los planos x e y, x y z, y y y z; estos orbitales se denominan (3d_ {xy} ), ) 3d_ {xz} ) y (3d_ {yz} ) orbitales, respectivamente. Un cuarto orbital d tiene lóbulos que se extienden a lo largo de los ejes xey; este es el orbital (3d_ {x ^ 2 − y ^ 2} ). El quinto orbital 3d, llamado orbital (3d_ {z ^ 2} ), tiene una forma única: parece un orbital (2p_z ) combinado con una rosquilla adicional de probabilidad de electrones en el plano xy. A pesar de su forma peculiar, el orbital (3d_ {z ^ 2} ) es matemáticamente equivalente a los otros cuatro y tiene la misma energía. A diferencia de los orbitales p, la fase de la función de onda para los orbitales d es la misma para pares opuestos de lóbulos. Como se muestra en la Figura ( PageIndex {5} ), la fase de la función de onda es positiva para los dos lóbulos del orbital (dz ^ 2 ) que se encuentran a lo largo del eje z, mientras que la fase de la función de onda es negativo para la rosquilla de densidad de electrones en el plano xy. Al igual que los orbitales syp, a medida que aumenta n, el tamaño de los orbitales d aumenta, pero las formas generales siguen siendo similares a las representadas en la Figura ( PageIndex {5} ).
f Orbitales (l = 3)
Los depósitos principales con n = 4 pueden tener subcapas con valores l = 3 y m l de −3, −2, −1, 0, +1, +2 y +3. Estas subcapas consisten en siete f orbitales. Cada orbital f tiene tres superficies nodales, por lo que sus formas son complejas. Debido a que los orbitales f no son particularmente importantes para nuestros propósitos, no los discutimos más a fondo, y los orbitales con valores más altos de l no se discuten en absoluto.
Energías orbitales
Aunque hemos discutido las formas de los orbitales, hemos dicho poco acerca de sus energías comparativas. Comenzamos nuestra discusión sobre energías orbitales considerando átomos o iones con un solo electrón (como H o He + ).
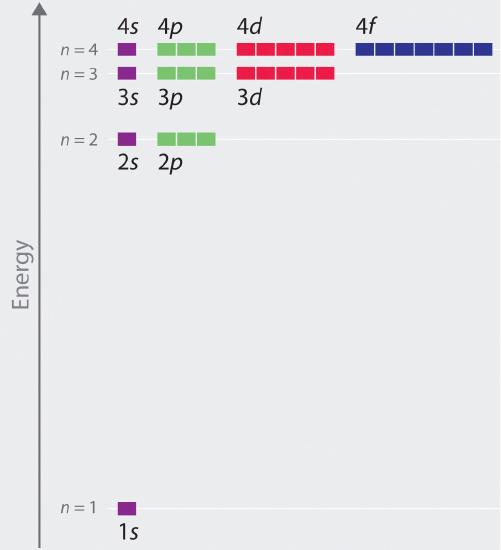
Las energías relativas de los orbitales atómicos con n ≤ 4 para un átomo de hidrógeno se representan en la Figura ( PageIndex {6} ); tenga en cuenta que las energías orbitales dependen de solamente el número cuántico principal n . En consecuencia, las energías de los orbitales 2 s y 2 p de hidrógeno son las mismas; las energías de los orbitales 3 s , 3 p y 3 d son las mismas; Etcétera. La mecánica cuántica predice que en el átomo de hidrógeno, todos los orbitales con el mismo valor de n (por ejemplo, los tres orbitales 2 p p) son degenerados , lo que significa que tener la misma energía Las energías orbitales obtenidas para el hidrógeno utilizando la mecánica cuántica son exactamente las mismas que las energías permitidas calculadas por Bohr. Sin embargo, en contraste con el modelo de Bohr, que permitía solo una órbita para cada nivel de energía, la mecánica cuántica predice que hay 4 orbitales con diferentes distribuciones de densidad electrónica en n = 2 capa principal (uno 2 s y tres 2 p orbitales), 9 en el n = 3 caparazón principal, y 16 [ 19459011] en el n = 4 shell principal. Los diferentes valores de l y m l para los orbitales individuales dentro de un caparazón principal dado no son importantes para comprender el Los espectros de emisión o absorción del átomo de hidrógeno en la mayoría de las condiciones, pero explican la división de las líneas principales que se observan cuando los átomos de hidrógeno se colocan en un campo magnético. La figura ( PageIndex {6} ) muestra que los niveles de energía se acercan cada vez más a medida que aumenta el valor de n , como se esperaba debido a 1 / n 2 dependencia de las energías orbitales.
Las energías de los orbitales en cualquier especie con un solo electrón pueden calcularse mediante una variación menor de la ecuación de Bohr , que puede extenderse a otras especies de un solo electrón incorporando la carga nuclear Z (el número de protones en el núcleo):
[E = – dfrac {Z ^ 2} {n ^ 2} Rhc label {6.6.1} ]
En general, tanto la energía como el radio disminuyen a medida que aumenta la carga nuclear. Por lo tanto, los orbitales más estables (aquellos con la energía más baja) son los más cercanos al núcleo. Por ejemplo, en el estado fundamental del átomo de hidrógeno, el electrón individual está en el orbital 1s, mientras que en el primer estado excitado, el átomo ha absorbido energía y el electrón ha sido promovido a uno de los orbitales n = 2. En iones con un solo electrón, la energía de un orbital dado depende solo de n, y de todas las subcapas dentro de una capa principal, como los orbitales (p_x ), (p_y ) y (p_z ), son degenerados
Resumen
Los cuatro tipos químicamente importantes de orbital atómico corresponden a valores de ( ell = 0 ), (1 ), (2 ) y (3 ). Los orbitales con ( ell = 0 ) son orbitales sy son esféricamente simétricos, con la mayor probabilidad de encontrar el electrón en el núcleo. Todos los orbitales con valores de (n> 1 ) y (ell = 0 ) contienen uno o más nodos. Los orbitales con ( ell = 1 ) son orbitales p y contienen un plano nodal que incluye el núcleo, dando lugar a una forma de mancuerna. Los orbitales con ( ell = 2 ) son orbitales d y tienen formas más complejas con al menos dos superficies nodales. Los orbitales con ( ell = 3 ) son f orbitales, que son aún más complejos.
Debido a que su distancia promedio del núcleo determina la energía de un electrón, cada orbital atómico con un conjunto dado de números cuánticos tiene una energía particular asociada, la energía orbital .
[E = – dfrac {Z ^ 2} {n ^ 2} Rhc
onumber ]
En los átomos o iones con un solo electrón, todos los orbitales con el mismo valor de (n ) tienen la misma energía (están degenerados), y las energías de las capas principales aumentan suavemente a medida que (n ) aumenta Se dice que un átomo o ion con el (los) electrón (es) en el (los) orbital (es) de energía más baja está en su estado fundamental, mientras que un átomo o ion en el que uno o más electrones ocupan orbitales de energía más alta se encuentra en un estado estado emocionado
Colaboradores
-
Modificado por Joshua Halpern ( Universidad de Howard )