Saltar al contenido
enlaces quimicos

6.E: Estructura electrónica de los átomos (ejercicios)

                 

 

 

 

 

 

 

 

 

Estos son ejercicios de tarea para acompañar el Mapa de texto creado para “Química: la ciencia central” por Brown et al. Se pueden encontrar bancos de preguntas de química general complementaria para otros mapas de texto y se puede acceder aquí . Además de estas preguntas disponibles públicamente, el acceso al banco privado de problemas para su uso en exámenes y tareas está disponible para los profesores solo de manera individual; comuníquese con Delmar Larsen para obtener una cuenta con permiso de acceso.

 

6.1: La naturaleza ondulatoria de la luz

 

 

Problemas conceptuales

 

  1. ¿Cuáles son las características de una ola? ¿Cuál es la relación entre la radiación electromagnética y la energía de las olas?
  2. A una longitud de onda constante, ¿qué efecto tiene el aumento de la frecuencia de una onda en su velocidad? su amplitud?
  3. Enumere las siguientes formas de radiación electromagnética en orden creciente de longitud de onda: rayos X, ondas de radio, ondas infrarrojas, microondas, ondas ultravioleta, ondas visibles y rayos gamma. Listelos en orden de frecuencia creciente. ¿Cuál tiene la mayor energía?
  4. Una gran industria se centra en el desarrollo de productos para el cuidado de la piel, como lociones bronceadoras y cosméticos, que no pueden ser penetrados por la radiación ultravioleta. ¿Cómo se compara la longitud de onda de la luz visible con la longitud de onda de la luz ultravioleta? ¿Cómo se compara la energía de la luz visible con la energía de la luz ultravioleta? ¿Por qué esta industria se centra en bloquear la luz ultravioleta en lugar de la luz visible?

    5.  

 

 

 

Problemas numéricos

 

  1. El ojo humano es sensible a qué fracción del espectro electromagnético, suponiendo un rango espectral típico de 10 4 a 10 20 Hz? Si viniéramos del planeta Krypton y tuviéramos una visión de rayos X (es decir, si nuestros ojos fueran sensibles a los rayos X además de la luz visible), ¿cómo cambiaría esta fracción?

  2. ¿Cuál es la frecuencia en megahercios correspondiente a cada longitud de onda?

    1. 755 m
    2. 6,73 nm
    3. 1.77 × 10 3 km
    4. 9,88 Å
    5. 3,7 × 10 −10 m

  3. ¿Cuál es la frecuencia en megahercios correspondiente a cada longitud de onda?

    1. 5,8 × 10 −7 m
    2. 2,3 Å
    3. 8,6 × 10 7 m
    4. 6,2 mm
    5. 3,7 nm

  4. También se observan espectros lineales para especies moleculares. Dadas las siguientes longitudes de onda características para cada especie, identifique la región espectral (ultravioleta, visible, etc.) en la que se producirán los siguientes espectros de línea. Dado 1.00 mol de cada compuesto y la longitud de onda de la luz absorbida o emitida, ¿a cuánta energía corresponde esto?

    1. NH 3 , 1,0 × 10 −2 m
    2. CH 3 CH 2 OH, 9,0 μm
    3. Átomo de Mo, 7,1 Å

  5. ¿Cuál es la velocidad de una ola en metros por segundo que tiene una longitud de onda de 1250 my una frecuencia de 2.36 × 10 5 s −1 ?

  6. Una onda viaja a 3.70 m / s con una frecuencia de 4.599 × 10 7 Hz y una amplitud de 1.0 m. ¿Cuál es su longitud de onda en nanómetros?

  7. Una estación de radio AM transmite con una longitud de onda de 248.0 m. ¿Cuál es la frecuencia de transmisión de la estación en kilohercios? Una estación de AM tiene un alcance de transmisión de 92.6 MHz. ¿Cuál es el rango de longitud de onda correspondiente en metros para esta recepción?

  8. Una estación de radio FM transmite con una longitud de onda de 3,21 m. ¿Cuál es la frecuencia de transmisión de la estación en megahercios? Una radio FM generalmente tiene un alcance de transmisión de 82-112 MHz. ¿Cuál es el rango de longitud de onda correspondiente en metros para esta recepción?

  9. Un horno de microondas funciona a una frecuencia de aproximadamente 2450 MHz. ¿Cuál es la longitud de onda correspondiente? El agua, con sus moléculas polares, absorbe la radiación electromagnética principalmente en la porción infrarroja del espectro. Dado este hecho, ¿por qué se utilizan hornos de microondas para cocinar alimentos?

    10.  

 

 

6.2: Energía cuantificada y fotones

 

 

 

Problemas conceptuales

 

 

  1. Describe la relación entre la energía de un fotón y su frecuencia.
  2. ¿Cómo se explicó la catástrofe ultravioleta?
  3. Si se permite que la radiación electromagnética con un rango continuo de frecuencias por encima del umbral de frecuencia de un metal golpee una superficie metálica, ¿la energía cinética de los electrones expulsados ​​es continua o cuantificada? Explica tu respuesta.
  4. Se dice que la energía vibracional de una cuerda de guitarra pulsada se cuantifica. ¿Qué queremos decir con esto? ¿Los sonidos emitidos por las 88 teclas de un piano también están cuantizados?
  5. ¿Cuál de los siguientes exhibe un comportamiento cuantificado: una voz humana, la velocidad de un automóvil, un arpa, los colores de la luz, el tamaño de los neumáticos de los automóviles, las olas de una lancha rápida?

    6.  

 

 

 

 

Respuestas conceptuales

 

  1. La energía de un fotón es directamente proporcional a la frecuencia de la radiación electromagnética.

  5. Cuantizado: arpa, tamaño de neumático, olas de lancha rápida; continuo: voz humana, colores de luz, velocidad del automóvil.

    6.  

 

 

 

Problemas numéricos

 

  1. ¿Cuál es la energía de un fotón de luz con cada longitud de onda? To which region of the electromagnetic spectrum does each wavelength belong?

    1. 4.33 × 10 5 m
    2. 0.065 nm
    3. 786 pm

  2. How much energy is contained in each of the following? To which region of the electromagnetic spectrum does each wavelength belong?

    1. 250 photons with a wavelength of 3.0 m
    2. 4.2 × 10 6 photons with a wavelength of 92 μm
    3. 1.78 × 10 22 photons with a wavelength of 2.1 Å

  3. A 6.023 x 10 23 photons are found to have an energy of 225 kJ. What is the wavelength of the radiation?

  4. Use the data in Table 2.1.1 to calculate how much more energetic a single gamma-ray photon is than a radio-wave photon. How many photons from a radio source operating at a frequency of 8 × 10 5 Hz would be required to provide the same amount of energy as a single gamma-ray photon with a frequency of 3 × 10 19 Hz?

  5. Use the data in Table 2.1.1 to calculate how much more energetic a single x-ray photon is than a photon of ultraviolet light.

  6. A radio station has a transmitter that broadcasts at a frequency of 100.7 MHz with a power output of 50 kW. Given that 1 W = 1 J/s, how many photons are emitted by the transmitter each second?

    7.  

 

 

Numerical Answers

 

    1. 4.59 × 10 −31 J/photon, radio
    2. 3.1 × 10 −15 J/photon, gamma ray
    3. 2.53 × 10 −16 J/photon, gamma ray

  3. 532 nm

    4.  

 

6.3: Line Spectra and the Bohr Model

 

 

Conceptual Problems

 

  1. Is the spectrum of the light emitted by isolated atoms of an element discrete or continuous? How do these spectra differ from those obtained by heating a bulk sample of a solid element? Explain your answers.

  2. Explain why each element has a characteristic emission and absorption spectra. If spectral emissions had been found to be continuous rather than discrete, what would have been the implications for Bohr’s model of the atom?

  3. Explain the differences between a ground state and an excited state. Describe what happens in the spectrum of a species when an electron moves from a ground state to an excited state. What happens in the spectrum when the electron falls from an excited state to a ground state?

  4. What phenomenon causes a neon sign to have a characteristic color? If the emission spectrum of an element is constant, why do some neon signs have more than one color?

  5. How is light from a laser different from the light emitted by a light source such as a light bulb? Describe how a laser produces light.

    6.  

 

 

Numerical Problems

 

  1. Using a Bohr model and the transition from n = 2 to n = 3 in an atom with a single electron, describe the mathematical relationship between an emission spectrum and an absorption spectrum. What is the energy of this transition? What does the sign of the energy value represent in this case? What range of light is associated with this transition?

  2. If a hydrogen atom is excited from an n = 1 state to an n = 3 state, how much energy does this correspond to? Is this an absorption or an emission? What is the wavelength of the photon involved in this process? To what region of the electromagnetic spectrum does this correspond?

  3. The hydrogen atom emits a photon with a 486 nm wavelength, corresponding to an electron decaying from the n = 4 level to which level? What is the color of the emission?

  4. An electron in a hydrogen atom can decay from the n = 3 level to n = 2 level. What is the color of the emitted light? What is the energy of this transition?

  5. Calculate the wavelength and energy of the photon that gives rise to the third line in order of increasing energy in the Lyman series in the emission spectrum of hydrogen. In what region of the spectrum does this wavelength occur? Describe qualitatively what the absorption spectrum looks like.

  6. The wavelength of one of the lines in the Lyman series of hydrogen is 121 nm. In what region of the spectrum does this occur? To which electronic transition does this correspond?

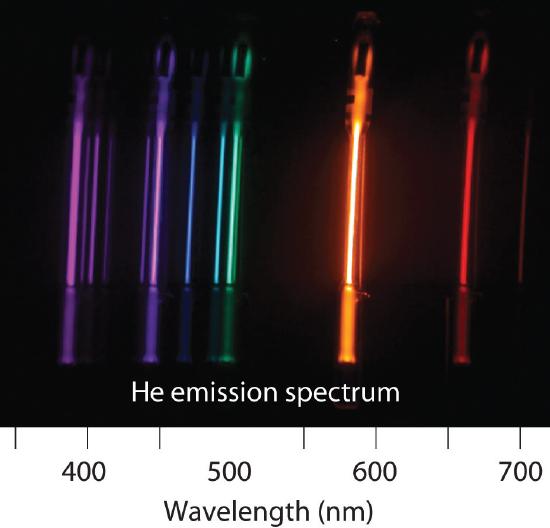
  7. The emission spectrum of helium is shown. Estimate what change in energy (Δ E ) gives rise to each line?

    6d97f47e1fbbbaf01e7f5aa0b64d0c70.jpg

  8. Removing an electron from solid potassium requires 222 kJ/mol. Would you expect to observe a photoelectric effect for potassium using a photon of blue light (λ = 485 nm)? What is the longest wavelength of energy capable of ejecting an electron from potassium? What is the corresponding color of light of this wavelength?

  9. The binding energy of an electron is the energy needed to remove an electron from its lowest energy state. According to Bohr’s postulates, calculate the binding energy of an electron in a hydrogen atom. There are 6.02 x 10 23 atoms in 1g of hydrogen atoms What wavelength in nanometers is required to remove such an electron from one hydrogen atom?

  10. As a radio astronomer, you have observed spectral lines for hydrogen corresponding to a state with n = 320, and you would like to produce these lines in the laboratory. Is this feasible? Why or why not?

    11.  

 

 

 

Numerical Answers

 

  1. 656 nm; red light

  3. n = 2, blue-green light

  5. 97.2 nm, 2.04 × 10 −18 J/photon, ultraviolet light, absorption spectrum is a single dark line at a wavelength of 97.2 nm

  7. Violet: 390 nm, 307 kJ/mol photons; Blue-purple: 440 nm, 272 kJ/mol photons; Blue-green: 500 nm, 239 kJ/mol photons; Orange: 580 nm, 206 kJ/mol photons; Red: 650 nm, 184 kJ/mol photons

  9. 1313 kJ/mol, λ ≤ 91.1 nm

    10.  

 

 

6.4: The Wave Behavior of Matter

 

 

 

Conceptual Problems

 

  1. Explain what is meant by each term and illustrate with a sketch:

    1. standing wave
    2. fundamental
    3. overtone
    4. node

  2. How does Einstein’s theory of relativity illustrate the wave–particle duality of light? What properties of light can be explained by a wave model? What properties can be explained by a particle model?

  3. In the modern theory of the electronic structure of the atom, which of de Broglie’s ideas have been retained? Which proved to be incorrect?

  4. According to Bohr, what is the relationship between an atomic orbit and the energy of an electron in that orbit? Is Bohr’s model of the atom consistent with Heisenberg’s uncertainty principle? Explain your answer.

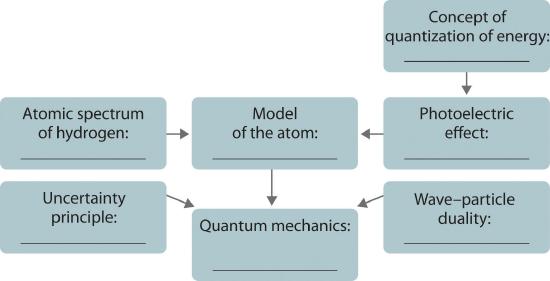
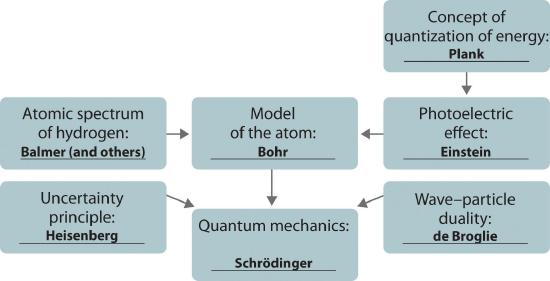
  5. The development of ideas frequently builds on the work of predecessors. Complete the following chart by filling in the names of those responsible for each theory shown.

    eec3edcba602abe7e6b3a4d10ea15e41.jpg

    6.  

 

 

 

Conceptual Answer

 

  5. 32f4a599188357c8486cf71b88736af3.jpg

    6.  

 

 

 

Numerical Problems

 

  1. How much heat is generated by shining a carbon dioxide laser with a wavelength of 1.065 μm on a 68.95 kg sample of water if 1.000 mol of photons is absorbed and converted to heat? Is this enough heat to raise the temperature of the water 4°C?

  2. Show the mathematical relationship between energy and mass and between wavelength and mass. What is the effect of doubling the

    1. mass of an object on its energy?
    2. mass of an object on its wavelength?
    3. frequency on its mass?

  3. What is the de Broglie wavelength of a 39 g bullet traveling at 1020 m/s ± 10 m/s? What is the minimum uncertainty in the bullet’s position?

  4. What is the de Broglie wavelength of a 6800 tn aircraft carrier traveling at 18 ± 0.1 knots (1 knot = 1.15 mi/h)? What is the minimum uncertainty in its position?

  5. Calculate the mass of a particle if it is traveling at 2.2 × 10 6 m/s and has a frequency of 6.67 × 10 7 Hz. If the uncertainty in the velocity is known to be 0.1%, what is the minimum uncertainty in the position of the particle?

  6. Determine the wavelength of a 2800 lb automobile traveling at 80 mi/h ± 3%. How does this compare with the diameter of the nucleus of an atom? You are standing 3 in. from the edge of the highway. What is the minimum uncertainty in the position of the automobile in inches?

    7.  

 

 

 

Numerical Answers

 

  1. E = 112.3 kJ, Δ T = 0.3893°C, over ten times more light is needed for a 4.0°C increase in temperature

  3. 1.7 × 10 −35 m, uncertainty in position is ≥ 1.4 × 10 −34 m

  5. 9.1 × 10 −39 kg, uncertainty in position ≥ 2.6 m

    6.  

 

 

6.5: Quantum Mechanics and Atomic Orbitals

 

 

 

Conceptual Problems

 

  1. Why does an electron in an orbital with n = 1 in a hydrogen atom have a lower energy than a free electron ( n = ∞)?

  2. What four variables are required to fully describe the position of any object in space? In quantum mechanics, one of these variables is not explicitly considered. Which one and why?

  3. Chemists generally refer to the square of the wave function rather than to the wave function itself. ¿Por qué?

  4. Orbital energies of species with only one electron are defined by only one quantum number. Which one? In such a species, is the energy of an orbital with n = 2 greater than, less than, or equal to the energy of an orbital with n = 4? Justify your answer.

  5. In each pair of subshells for a hydrogen atom, which has the higher energy? Give the principal and the azimuthal quantum number for each pair.

    1. 1 s , 2 p
    2. 2 p , 2 s
    3. 2 s , 3 s
    4. 3 d , 4 s

  6. What is the relationship between the energy of an orbital and its average radius? If an electron made a transition from an orbital with an average radius of 846.4 pm to an orbital with an average radius of 476.1 pm, would an emission spectrum or an absorption spectrum be produced? ¿Por qué?

  7. In making a transition from an orbital with a principal quantum number of 4 to an orbital with a principal quantum number of 7, does the electron of a hydrogen atom emit or absorb a photon of energy? What would be the energy of the photon? To what region of the electromagnetic spectrum does this energy correspond?

  8. What quantum number defines each of the following?

    1. the overall shape of an orbital
    2. the orientation of an electron with respect to a magnetic field
    3. the orientation of an orbital in space
    4. the average energy and distance of an electron from the nucleus

  9. In an attempt to explain the properties of the elements, Niels Bohr initially proposed electronic structures for several elements with orbits holding a certain number of electrons, some of which are in the following table:

    Element Number of Electrons Electrons in orbits with n =
    4 3 2 1
    H 1 1
    He 2 2
    Ne 10 8 2
    Ar 18 8 8 2
    Li 3 1 2
    Na 11 1 8 2
    K 19 1 8 8 2
    Be 4 2 2
    1. Draw the electron configuration of each atom based only on the information given in the table. What are the differences between Bohr’s initially proposed structures and those accepted today?
    2. Using Bohr’s model, what are the implications for the reactivity of each element?
    3. Give the actual electron configuration of each element in the table.

    10.  

 

 

 

Numerical Problems

 

  1. How many subshells are possible for n = 3? What are they?

  2. How many subshells are possible for n = 5? What are they?

  3. What value of l corresponds to a d subshell? How many orbitals are in this subshell?

  4. What value of l corresponds to an f subshell? How many orbitals are in this subshell?

  5. State the number of orbitals and electrons that can occupy each subshell.

    1. 2 s
    2. 3 p
    3. 4 d
    4. 6 f

  6. State the number of orbitals and electrons that can occupy each subshell.

    1. 1 s
    2. 4 p
    3. 5 d
    4. 4 f

  7. How many orbitals and subshells are found within the principal shell n = 6? How do these orbital energies compare with those for n = 4?

  8. How many nodes would you expect a 4 p orbital to have? A 5 s orbital?

  9. A p orbital is found to have one node in addition to the nodal plane that bisects the lobes. What would you predict to be the value of n ? If an s orbital has two nodes, what is the value of n ?

    10.  

 

 

Numerical Answers

 

  1. Three subshells, with l = 0 ( s ), l = 1 ( p ), and l = 2 ( d ).

  3. A d subshell has l = 2 and contains 5 orbitals.

    1. 2 electrons; 1 orbital
    2. 6 electrons; 3 orbitals
    3. 10 electrons; 5 orbitals
    4. 14 electrons; 7 orbitals

  7. A principal shell with n = 6 contains six subshells, with l = 0, 1, 2, 3, 4, and 5, respectively. These subshells contain 1, 3, 5, 7, 9, and 11 orbitals, respectively, for a total of 36 orbitals. The energies of the orbitals with n = 6 are higher than those of the corresponding orbitals with the same value of l for n = 4.

    8.  

 

6.6: Representation of Orbitals

 

 

 

6.7: Many-Electron Atoms

 

 

 

Conceptual Problems

 

  1. A set of four quantum numbers specifies each wave function. What information is given by each quantum number? What does the specified wave function describe?

  2. List two pieces of evidence to support the statement that electrons have a spin.

  3. The periodic table is divided into blocks. Identify each block and explain the principle behind the divisions. Which quantum number distinguishes the horizontal rows?

  4. Identify the element with each ground state electron configuration.

    1. [He]2 s 2 2 p 3
    2. [Ar]4 s 2 3 d 1
    3. [Kr]5 s 2 4 d 10 5 p 3
    4. [Xe]6 s 2 4 f 6

  5. Identify the element with each ground state electron configuration.

    1. [He]2 s 2 2 p 1
    2. [Ar]4 s 2 3 d 8
    3. [Kr]5 s 2 4 d 10 5 p 4
    4. [Xe]6 s 2

  6. Propose an explanation as to why the noble gases are inert.

    7.  

 

 

 

Numerical Problems

 

  1. How many magnetic quantum numbers are possible for a 4 p subshell? A 3 d subshell? How many orbitals are in these subshells?

  2. How many magnetic quantum numbers are possible for a 6 s subshell? A 4 f subshell? How many orbitals does each subshell contain?

  3. If l = 2 and m l = 2, give all the allowed combinations of the four quantum numbers ( n , l , m l , m s ) for electrons in the corresponding 3 d subshell.

  4. Give all the allowed combinations of the four quantum numbers ( n , l , m l , m s ) for electrons in a 4 d subshell. How many electrons can the 4 d orbital accommodate? How would this differ from a situation in which there were only three quantum numbers ( n , l , m )?

  5. Given the following sets of quantum numbers ( n , l , m l , m s ), identify each principal shell and subshell.

    1. 1, 0, 0, ½
    2. 2, 1, 0, ½
    3. 3, 2, 0, ½
    4. 4, 3, 3, ½

  6. Is each set of quantum numbers allowed? Explain your answers.

    1. n = 2; l = 1; m l = 2; m s = +½
    2. n = 3, l = 0; m l = −1; m s = −½
    3. n = 2; l = 2; m l = 1; m s = +½
    4. n = 3; l = 2; m l = 2; m s = +½

  7. List the set of quantum numbers for each electron in the valence shell of each element.

    1. beryllium
    2. xenon
    3. lithium
    4. fluorine

  8. List the set of quantum numbers for each electron in the valence shell of each element.

    1. carbon
    2. magnesium
    3. bromine
    4. sulfur

  9. Sketch the shape of the periodic table if there were three possible values of m s for each electron (+½, −½, and 0); assume that the Pauli principle is still valid.

  10. Predict the shape of the periodic table if eight electrons could occupy the p subshell.

  11. If the electron could only have spin +½, what would the periodic table look like?

  12. If three electrons could occupy each s orbital, what would be the electron configuration of each species?

    1. sodium
    2. titanium
    3. fluorine
    4. calcium

  13. If Hund’s rule were not followed and maximum pairing occurred, how many unpaired electrons would each species have? How do these numbers compare with the number found using Hund’s rule?

    1. phosphorus
    2. iodine
    3. manganese

  14. Write the electron configuration for each element in the ground state.

    1. aluminum
    2. calcium
    3. sulfur
    4. tin
    5. nickel
    6. tungsten
    7. neodymium
    8. americium

  15. Write the electron configuration for each element in the ground state.

    1. boron
    2. rubidium
    3. bromine
    4. germanium
    5. vanadium
    6. palladium
    7. bismuth
    8. europium

  16. Give the complete electron configuration for each element.

    1. magnesium
    2. potassium
    3. titanium
    4. selenium
    5. iodine
    6. uranium
    7. germanium

  17. Give the complete electron configuration for each element.

    1. tin
    2. copper
    3. fluorine
    4. hydrogen
    5. thorium
    6. yttrium
    7. bismuth

  18. Write the valence electron configuration for each element:

    1. samarium
    2. praseodymium
    3. boron
    4. cobalt

  19. Using the Pauli exclusion principle and Hund’s rule, draw valence orbital diagrams for each element.

    1. barium
    2. neodymium
    3. iodine

  20. Using the Pauli exclusion principle and Hund’s rule, draw valence orbital diagrams for each element.

    1. chlorine
    2. silicon
    3. scandium

  21. How many unpaired electrons does each species contain?

    1. lead
    2. cesium
    3. copper
    4. silicon
    5. selenium

  22. How many unpaired electrons does each species contain?

    1. helium
    2. oxygen
    3. bismuth
    4. silver
    5. boron

  23. For each element, give the complete electron configuration, draw the valence electron configuration, and give the number of unpaired electrons present.

    1. lithium
    2. magnesium
    3. silicon
    4. cesium
    5. lead

  24. Use an orbital diagram to illustrate the aufbau principle, the Pauli exclusion principle, and Hund’s rule for each element.

    1. carbon
    2. sulfur

    25.  

 

 

Numerical Answers

 

  1. For a 4 p subshell, n = 4 and l = 1. The allowed values of the magnetic quantum number, ml , are therefore +1, 0, −1, corresponding to three 4 p orbitals. For a 3 d subshell, n = 3 and l = 2. The allowed values of the magnetic quantum number, ml , are therefore +2, +1, 0, −1, −2, corresponding to five 3 d orbitals.

    2.  

 

6.8: Electron Configurations

 

 

 

6.9: Electron Configurations and the Periodic Table

 

                     

 

             

Post Views: 13