¿Alguna vez calculó una distancia “bajando”, es decir, contando la cantidad de pasos necesarios para tomar una cierta distancia? O quizás ha usado el ancho de su mano, o la distancia desde su codo hasta la punta de un dedo para comparar dos dimensiones. Si es así, te has comprometido en lo que probablemente sea el primer tipo de medición que haya realizado la humanidad primitiva. Los resultados de una medición siempre se expresan en algún tipo de escala que se define en términos de un tipo particular de unidad . Las primeras escalas de distancia probablemente estaban relacionadas con el cuerpo humano, ya sea directamente (la longitud de una extremidad) o indirectamente (la distancia que un hombre podía caminar en un día).
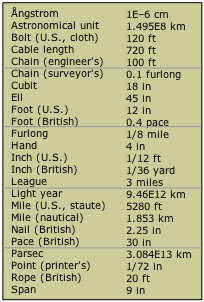
A medida que se desarrollaba la civilización, surgió una amplia variedad de escalas de medición, muchas por la misma cantidad (como la longitud), pero adaptadas a actividades u oficios particulares. Eventualmente, se hizo evidente que para que el comercio fuera posible, estas escalas tenían que definirse en términos de estándares que permitieran verificar las medidas y, cuando se expresaban en diferentes unidades (bushels y picotazos, por ejemplo), para ser correlacionado o convertido.
El evento más influyente en la historia de la medición fue, sin duda, la Revolución Francesa y la Era de la Racionalidad que siguió. Esto condujo directamente al sistema métrico que intentó eliminar la confusa multiplicidad de escalas de medición reduciéndolas a unas pocas fundamentales que podrían combinarse para expresar cualquier tipo de cantidad. El sistema métrico se extendió rápidamente por gran parte del mundo, y eventualmente incluso a Inglaterra y al resto del Reino Unido cuando ese país estableció vínculos económicos más estrechos con Europa en la última parte del siglo XX. Estados Unidos es actualmente el único país importante en el que la “metricación” ha progresado poco en su propia sociedad, probablemente debido a su relativo aislamiento geográfico y su vibrante economía interna.
La ciencia, siendo un esfuerzo verdaderamente internacional, adoptó la medición métrica muy pronto; La ingeniería y las tecnologías relacionadas han sido más lentas para realizar este cambio, pero lo están haciendo gradualmente. Sin embargo, incluso dentro del sistema métrico, se empleó una variedad de unidades para medir la misma cantidad fundamental; por ejemplo, la energía podría expresarse dentro del sistema métrico en unidades de ergios, electronvoltios, julios y dos tipos de calorías. Esto condujo, a mediados de la década de 1960, a la adopción de un conjunto más básico de unidades, las unidades Systeme Internationale ( SI ) que ahora se reconocen como El estándar para la ciencia y, cada vez más, para la tecnología de todo tipo.
Los Siete SI Unidades base y prefijos decimales
En principio, cualquier cantidad física puede expresarse en términos de solo siete unidades base (Tabla ( PageIndex {1} )), con cada unidad base definida por un estándar descrito en el sitio web NIST [ 19459027].
| Propiedad | Unidad | Símbolo |
|---|---|---|
| longitud | metro | m |
| masa | kilogramo | kg |
| hora | segundo | s |
| temperatura (absoluta) | Kelvin | K |
| cantidad de sustancia | topo | mol |
| corriente eléctrica | amperios | A |
| intensidad luminosa | candela | cd |
Vale la pena señalar algunos puntos especiales sobre algunas de estas unidades:
- La unidad base de masa es única en el sentido de que se incluye un prefijo decimal (Tabla ( PageIndex {2} )); es decir, la unidad base SI no es el gramo .
- La unidad base del tiempo es la única que no es métrica. Numerosos intentos de lograrlo nunca han tenido éxito; Todavía estamos atrapados con el sistema 24:60:60 que heredamos de la antigüedad. Los antiguos egipcios de alrededor de 1500 aC inventaron el día de 12 horas, y la parte 60:60 es un remanente del sistema de base 60 que los sumerios usaron para sus cálculos astronómicos alrededor de 100 aC.
- De especial interés para la Química es el mol , la unidad base para expresar la cantidad de materia . Aunque el número no se menciona explícitamente en la definición oficial, los químicos definen el lunar como el número de Avogadro (aproximadamente 6.02×10 23 ) de cualquier cosa.
Debido a la amplia gama de valores que pueden tener las cantidades, ha sido una práctica habitual emplear prefijos como mili y mega para indicar fracciones decimales y múltiplos de unidades métricas. Como parte del estándar SI, este sistema se ha ampliado y formalizado (Tabla ( PageIndex {2} )).
| Prefijo | Abreviatura | Multiplicador | Prefijo | Abreviatura | Multiplicador |
|---|---|---|---|---|---|
| peta | P | 10 18 | deci | s | 10 –1 |
| tera | T | 10 12 | centi | c | 10 –2 |
| giga | G | 10 9 | milli | m | 10 –3 |
| mega | M | 10 6 | micro | μ | 10 –6 |
| kilo | k | 10 3 | nano | n | 10 –9 |
| hecto | h | 10 2 | pico | p | 10 –12 |
| deca | da | 10 | femto | f | 10 –15 |
Unidades y dimensiones derivadas
La mayoría de las cantidades físicas con las que realmente tratamos en la ciencia y también en nuestra vida diaria, tienen unidades propias: volumen, presión, energía y resistencia eléctrica son solo algunos de los cientos de ejemplos posibles. Sin embargo, es importante entender que todo esto puede expresarse en términos de las unidades de base del SI; en consecuencia se conocen como unidades derivadas . De hecho, la mayoría de las cantidades físicas se pueden expresar en términos de una o más de las siguientes cinco unidades fundamentales:
- masa (M)
- longitud (L)
- hora (T)
- carga eléctrica (Q)
- temperatura (Θ theta)
Considere, por ejemplo, la unidad de volumen , que denotamos como V. Para medir el volumen de una caja rectangular, necesitamos multiplicar las longitudes medidas a lo largo de las tres coordenadas:
[V = x · y · z ]
Decimos, por lo tanto, que el volumen tiene las dimensiones de cubos de longitud:
[dim {V } = L ^ 3 ]
Por lo tanto, las unidades de volumen serán m 3 (en el SI) o cm 3 , ft 3 (inglés), etc. Además, cualquier la fórmula que calcula un volumen debe contener la dimensión L 3 ; así, el volumen de una esfera es (4/3 πr ^ 3 ). Las dimensiones de una unidad son las potencias que M, L, t, Q y Q se deben dar para expresar la unidad. Por lo tanto,
[dim {V } = M ^ 0L ^ 3T ^ 0Q ^ 0 Θ ^ 0 ]
como se indicó anteriormente.
Hay varias razones por las que vale la pena considerar las dimensiones de una unidad.
- Quizás el uso más importante de las dimensiones es ayudarnos a comprender las relaciones entre varias unidades de medida y, por lo tanto, obtener una mejor comprensión de su significado físico. Por ejemplo, una mirada a las dimensiones de los términos eléctricos frecuentemente confundidos resistencia y resistividad debería permitirle explicar, en palabras simples, la diferencia entre ellos.
- De la misma manera, las dimensiones esencialmente te dicen cómo calcular cualquiera de estas cantidades, usando las unidades específicas que desees. (Tenga en cuenta aquí la distinción entre dimensiones y unidades).
- Así como no puedes agregar manzanas a las naranjas, una expresión como (a = b + cx ^ 2 ) no tiene sentido a menos que las dimensiones de cada lado sean idénticas. (Por supuesto, las dos partes también deberían trabajar en las mismas unidades).
- Muchas cantidades deben ser adimensionales, por ejemplo, la variable x en expresiones como ( log x ), (e ^ x ) y ( sin x ). Verificar las dimensiones de tal cantidad puede ayudar a evitar errores.
El estudio formal y detallado de las dimensiones se conoce como análisis dimensional y es un tema en cualquier curso de física básica.
|
Q
|
M
|
L
|
t | cantidad | Unidad SI, otras unidades típicas |
|---|---|---|---|---|---|
| 1 | – | – | – | carga eléctrica | coulomb |
| – | 1 | – | – | masa | kilogramo, gramo, tonelada métrica, libra |
| – | – | 1 | – | longitud | metro, pie, milla |
| – | – | – | 1 | hora | segundo, día, año |
| – | – | 3 | – | volumen | litro, cm 3 , cuarto de galón, fluidounce |
| – | 1 | –3 | – | densidad | kg m –3 , g cm –3 |
| – | 1 | 1 | –2 | fuerza | newton, dyne |
| – | 1 | –1 | –2 | presión | pascal, atmósfera, torr |
| – | 1 | 2 | –2 | energía | joule, erg, caloría, electronvoltio |
| – | 1 | 2 | –3 | poder | vatios |
| 1 | 1 | 2 | –2 | potencial eléctrico | voltios |
| 1 | – | – | –1 | corriente eléctrica | amperios |
| 1 | 1 | 1 | –2 | intensidad del campo eléctrico | voltios m –1 |
| –2 | 1 | 2 | –1 | resistencia eléctrica | ohm |
| 2 | 1 | 3 | –1 | resistividad eléctrica | – |
| 2 | –1 | –2 | 1 | conductancia eléctrica | siemens, mho |
El análisis dimensional se emplea ampliamente cuando es necesario convertir un tipo de unidad en otra, y los estudiantes de química a menudo lo usan en cálculos de “aritmética química”, en cuyo contexto también se lo conoce como el método de “Etiqueta de factor”. En esta sección, veremos algunas de las cantidades que se encuentran ampliamente en Química, y en las unidades en las que se expresan comúnmente. Al hacerlo, también consideraremos el rango real de valores que estas cantidades pueden asumir, tanto en la naturaleza en general, como también dentro del subconjunto de la naturaleza que la química normalmente aborda. Al examinar las diversas unidades de medida, es interesante observar que sus valores unitarios se establecen cerca de los que se encuentran en la experiencia humana cotidiana
La masa no es peso
Estas dos cantidades están muy confundidas. Aunque a menudo se usan como sinónimos en el habla y la escritura informales, tienen diferentes dimensiones: peso es la fuerza ejercida sobre una masa por el campo gravacional local:
[f = m a = m g label {Eq1} ]
donde g es la aceleración de la gravedad. Mientras que el valor nominal de la última cantidad es de 9.80 m s –2 en la superficie de la Tierra, su valor exacto varía localmente. Debido a que es una fuerza, la unidad de peso del SI es propiamente el newton , pero es una práctica común (¡excepto en las clases de física!) Usar los términos “peso” y “masa” indistintamente, entonces las unidades kilogramos y gramos son aceptables en casi todos los contextos de laboratorio ordinarios.
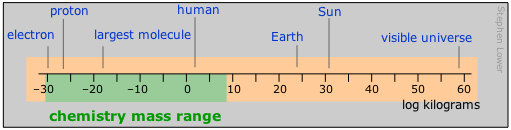
Tenga en cuenta que en este diagrama y en los que siguen, la escala numérica representa el logaritmo del número que se muestra. Por ejemplo, la masa del electrón es 10 –30 kg.
El rango de masas abarca 90 órdenes de magnitud, más que cualquier otra unidad. El rango con el que normalmente se ocupa la química se ha ampliado enormemente desde los días en que un microgramo era una cantidad de material casi inconcebiblemente pequeña para manejar en el laboratorio; Este límite inferior ahora ha caído al nivel atómico con el desarrollo de herramientas para manipular directamente estas partículas. El nivel superior refleja las masas más grandes que se manejan en operaciones industriales, pero en los campos recientemente desarrollados de geoquímica y química ambiental, el rango puede extenderse indefinidamente. Los flujos de elementos entre las diversas regiones del medio ambiente (atmósfera a los océanos, por ejemplo) a menudo se citan en teragramas.
Longitud
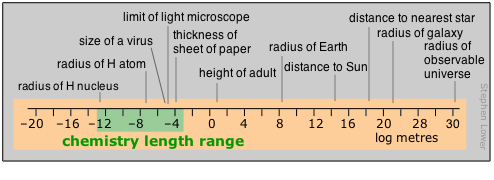
Los químicos tienden a trabajar principalmente en la parte moderadamente pequeña del rango de distancia. Aquellos que viven en el mundo liliputiense de estructuras cristalinas y moleculares y radios atómicos encuentran que el picómetro es una moneda conveniente, pero aún se ve la unidad anterior no-SI llamada Ångstrom utilizada en este contexto; 1Å = 10 –10 m = 100pm. La nanotecnología, la furia de la era actual, también reside en este ámbito. Las moléculas poliméricas y coloides más grandes definen el extremo superior del rango de partículas; más allá de eso, en el mundo normal de hacer cosas en el laboratorio, el centímetro y ocasionalmente el milímetro comúnmente gobiernan.
Tiempo
Para los humanos, el tiempo se mueve por el latido del corazón; más allá de eso, son los movimientos de nuestro planeta los que cuentan las horas, días y años que eventualmente definen nuestras vidas. Más allá de los pocos miles de años de historia detrás de nosotros, esos años a los poderes de decenas que son la tarifa para campos como la biología evolutiva, la geología y la cosmología, dejan de transmitir ningún significado real para nosotros. Quizás es por eso que tanta gente no está muy inclinada a aceptar su validez.
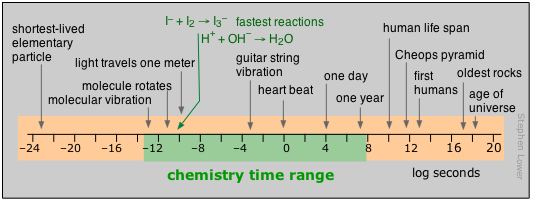
La mayor parte de lo que realmente tiene lugar en el tubo de ensayo del químico opera en una escala de tiempo mucho más corta, aunque no hay límite en cuanto a la lentitud de una reacción; Los límites superiores de aquellos que podemos estudiar directamente en el laboratorio están determinados en parte por cuánto tiempo puede esperar un estudiante graduado antes de pasar a un empleo remunerado. Al observar el mundo microscópico de los átomos y las moléculas, la escala de tiempo nuevamente nos traslada a un mundo irreal donde los números tienden a perder su significado. Puede obtener cierta apreciación de la duración de un nanosegundo si observa que se trata del tiempo que tarda un rayo de luz en viajar entre sus dos manos extendidas. En cierto sentido, los fundamentos materiales de la química en sí están definidos por el tiempo: ni un elemento nuevo ni una molécula pueden reconocerse como tales a menos que duren lo suficiente como para que se tome su “imagen” a través de la medición de sus propiedades distintivas.
Temperatura
La temperatura, la medida de la intensidad térmica, abarca el rango más estrecho de cualquiera de las unidades base de la caja de herramientas de medición del químico. La razón de esto está ligada al significado de la temperatura como una medida de la intensidad de la energía cinética térmica. El cambio químico ocurre cuando los átomos se empujan a nuevos arreglos, y la debilidad de estos movimientos detiene la mayor parte de la química a medida que se acerca al cero absoluto. En el extremo superior de la escala, los movimientos térmicos se vuelven lo suficientemente vigorosos como para sacudir las moléculas en átomos y, finalmente, como en las estrellas, eliminar los electrones, dejando un fluido gaseoso, o plasma, esencialmente sin reacción, de núcleos (iones) desnudos y electrones

El grado es realmente un incremento de temperatura, una fracción fija de la distancia entre dos puntos de referencia definidos en una escala de temperatura .
Cuando decimos que la temperatura es tantos grados, debemos especificar la escala particular en la que expresamos esa temperatura. Una escala de temperatura tiene dos características definitorias, las cuales se pueden elegir arbitrariamente:
- La temperatura que corresponde a 0 ° en la escala;
- La magnitud del incremento de la unidad de temperatura, es decir, el tamaño del grado .
Para expresar una temperatura dada en una escala en términos de otra, es necesario tener en cuenta estos dos factores. La clave para las conversiones de temperatura es fácil si tiene en cuenta que entre los llamados puntos de hielo y vapor de agua hay 180 grados Fahrenheit, pero solo 100 grados Celsius, lo que hace que el F ° 100/180 = 5/9 magnitud de la C °. Observe la distinción entre “° C” (una temperatura ) y “C °” (un incremento de temperatura ). Debido a que el punto de hielo está a 32 ° F, las dos escalas están compensadas por esta cantidad. Si recuerda esto, no es necesario memorizar una fórmula de conversión; puedes resolverlo cuando lo necesites.
Cerca del final del siglo XIX, cuando se comenzó a comprender el significado físico de la temperatura, se sintió la necesidad de una escala de temperatura cuyo cero realmente significa cero, es decir, la ausencia total de movimiento térmico. Esto dio lugar a la escala de temperatura absoluta cuyo punto cero es –273,15 ° C, pero que conserva el mismo grado de magnitud que la escala Celsius. Esto finalmente cambió su nombre por Lord Kelvin (William Thompson); así, el grado Celsius se convirtió en el kelvin . Por lo tanto, ahora podemos expresar un incremento como cinco C ° como “cinco Kelvin”
La importancia de las escalas de temperatura absoluta es que las temperaturas absolutas se pueden ingresar directamente en todas las fórmulas fundamentales de física y química en las que la temperatura es una variable.
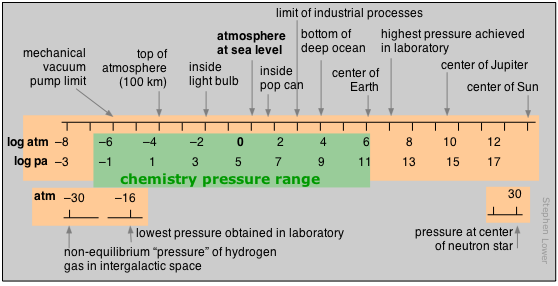
Presión
La presión es la medida de la fuerza ejercida sobre un área unitaria de superficie. Por lo tanto, sus unidades SI son newtons por metro cuadrado, pero hacemos un uso tan frecuente de la presión que una unidad SI derivada, el pascal , se usa comúnmente:
[1 ; Pa = 1 ; N ; m ^ {- 2} ]
El concepto de presión se desarrolló por primera vez en relación con estudios relacionados con la atmósfera y el vacío que se llevaron a cabo en el siglo XVII.
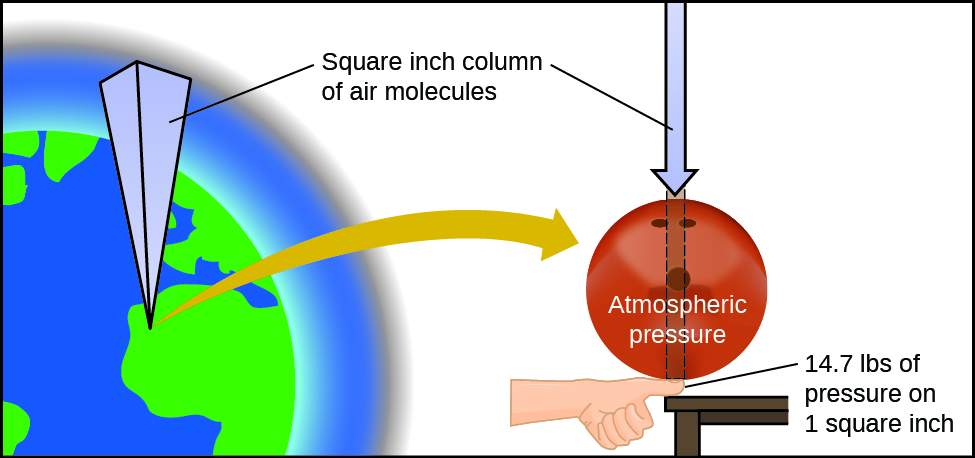
La presión atmosférica es causada por el peso de la columna de moléculas de aire en la atmósfera sobre un objeto, como el vagón cisterna debajo. Al nivel del mar, esta presión es más o menos la misma que ejerce un elefante africano adulto de pie sobre un felpudo, o una bola de boliche típica que descansa sobre la uña del pulgar. Estas pueden parecer grandes cantidades, y lo son, pero la vida en la Tierra ha evolucionado bajo tanta presión atmosférica. Si realmente posas una bola de boliche en tu uña del pulgar, la presión experimentada es el doble de la presión habitual, y la sensación es desagradable.
Video ( PageIndex {1} ) : Se proporciona una ilustración dramática de la presión atmosférica en Este breve video, que muestra un vagón cisterna implosionando cuando su presión interna disminuye. Se explica brevemente una demostración a menor escala de este fenómeno.
Las moléculas de un gas se encuentran en un estado de movimiento térmico constante, moviéndose en línea recta hasta experimentar una colisión que intercambia el impulso entre pares de moléculas y las envía rebotando en otras direcciones. Esto conduce a una distribución completamente aleatoria de las velocidades moleculares, tanto en velocidad como en dirección, o lo haría en ausencia del campo gravitacional de la Tierra, que ejerce una pequeña fuerza hacia abajo sobre cada molécula, dando a los movimientos en esa dirección una ventaja muy leve. En un contenedor ordinario, este efecto es demasiado pequeño para ser notable, pero en una columna de aire muy alta el efecto se suma: las moléculas en cada capa vertical experimentan más golpes dirigidos hacia abajo de los que están por encima. La fuerza resultante se aleatoriza rápidamente, lo que resulta en una mayor presión en esa capa que luego se propaga hacia abajo en las capas inferiores.
Al nivel del mar, la masa total del mar de aire presionando hacia abajo en cada 1 cm 2 de superficie es de aproximadamente 1034 go 10340 kg m –2 . La fuerza (peso) que la aceleración gravitacional de la Tierra g ejerce sobre esta masa es
[f = ma = mg = (10340 ; kg) (9.81 ; m ; s ^ {- 2}) = 1.013 veces 10 ^ 5 ; kg ; m ; s ^ {- 2} = 1.013 por 10 ^ 5 ; N ]
resultando en una presión de 1.013 × 10 5 nm –2 = 1.013 × 10 5 Pa. La presión real al nivel del mar varía con las condiciones atmosféricas , por lo que es habitual definir la presión atmosférica estándar como 1 atm = 1.01325 x 10 5 Pa o 101.325 kPa. Aunque la atmósfera estándar no es una unidad SI, todavía se emplea ampliamente. En meteorología, a menudo se usa la barra , exactamente 1.000 × 10 5 = 0.967 atm.
Summary
The natural sciences begin with observation , and this usually involves numerical measurements of quantities such as length, volume, density, and temperature. Most of these quantities have units of some kind associated with them, and these units must be retained when you use them in calculations. Measuring units can be defined in terms of a very small number of fundamental ones that, through “dimensional analysis”, provide insight into their derivation and meaning, and must be understood when converting between different unit systems.
Contributions
-
Stephen Lower, Professor Emeritus ( Simon Fraser U. ) Chem1 Virtual Textbook
-
Paul Flowers (University of North Carolina – Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd…a7ac8df6@9.110 ).