El producto de la intensidad y el área del campo eléctrico es el flujo ( Phi_E ). Mientras que (E ) es una cantidad intensiva , ( Phi_E ) es una cantidad extensa . Sus dimensiones son ML 3 T – 2 Q – 1 y sus unidades SI son N m [19459005 ] 2 C – 1 , aunque más tarde, después de conocer la unidad llamada volt , preferiremos expresar ( Phi_E ) en V m.
Con grados crecientes de sofisticación, el flujo puede definirse matemáticamente como:
[ Phi_E = EA ] [19459009 ]
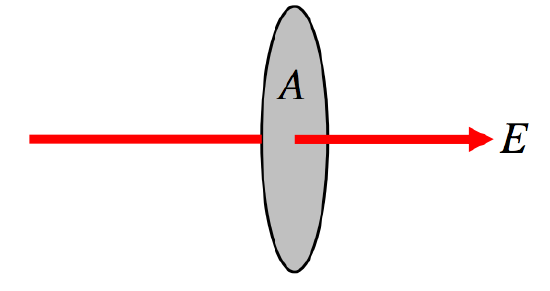
( text {FIGURE I.4} ): Flujo que es perpendicular a la superficie.
[ Phi_E = EA cos theta = textbf {E} cdot textbf {A} ]
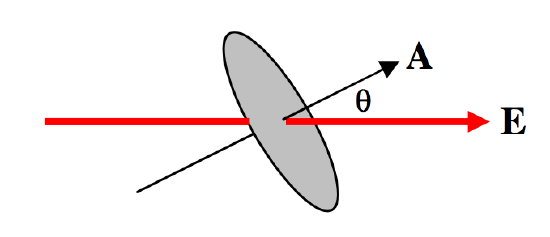
( text {FIGURE I.5} ): Flujo que está en ángulo con la superficie.
Tenga en cuenta que ( textbf {E} ) es un vector, pero ( Phi_E ) es un escalar.
[ Phi_E = iint textbf {E} cdot d textbf {A} ]
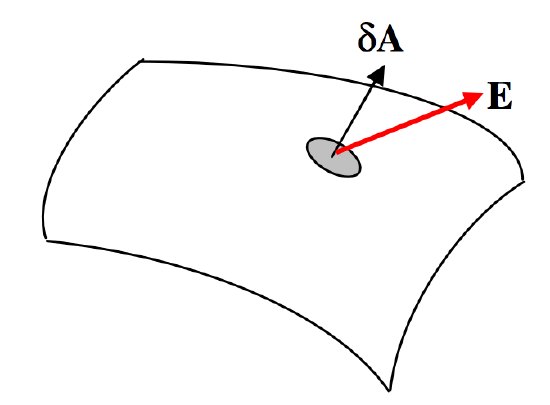
[ 19459002] ( text {FIGURA I.6} )
También podemos definir un (D ) – flujo por
[19459002 ] [ Phi_D = iint textbf {D} cdot d textbf {A}. ]
Las dimensiones de ( Phi_D ) son solo (Q ) y las unidades SI son coulombs (C).
Un ejemplo está en orden:
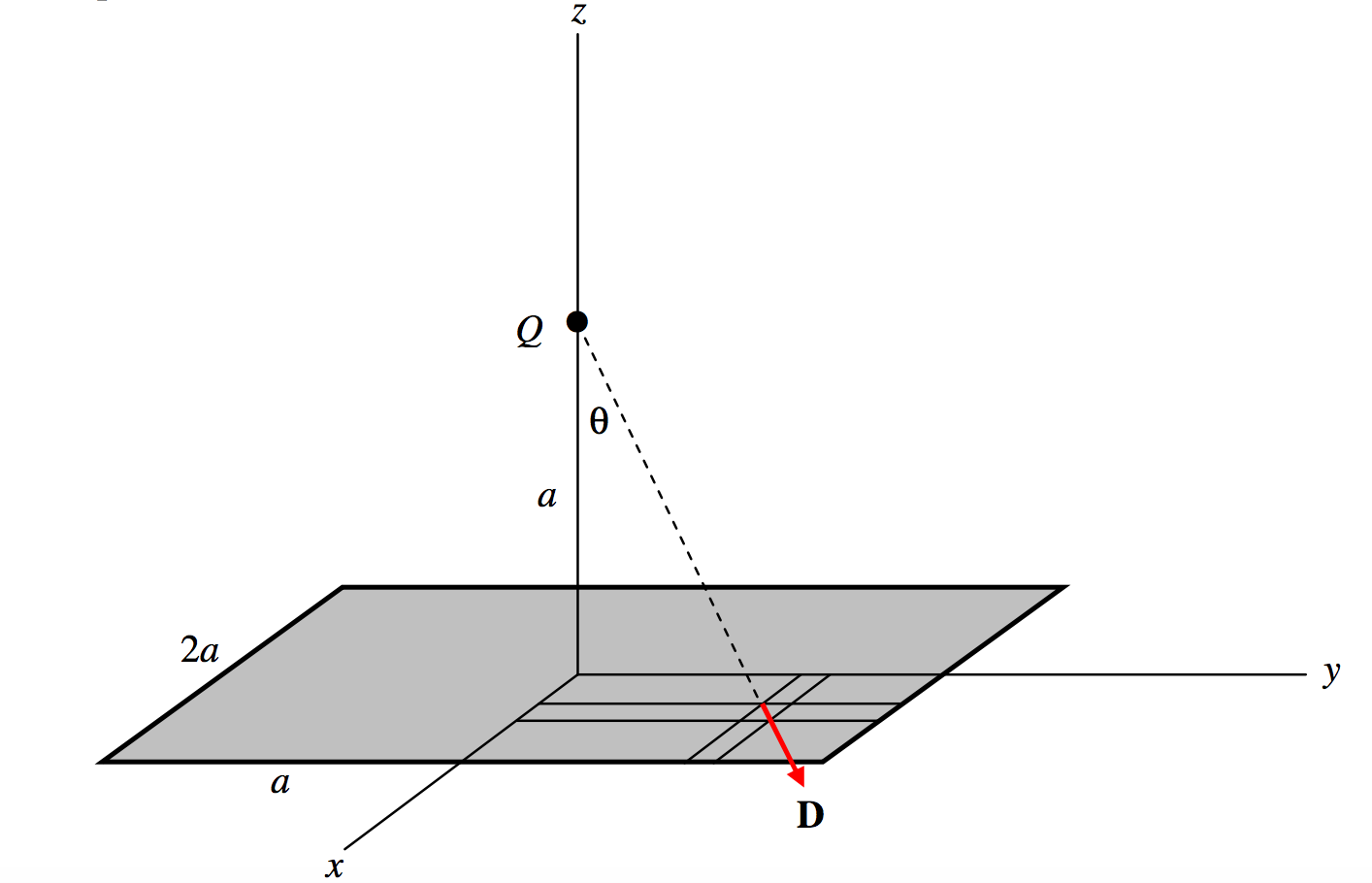
( text {FIGURE I.7} ) [19459008 ]
Considere un cuadrado de lado (2a ) en el plano xy como se muestra. Supongamos que hay una carga positiva (Q ) a una altura (a ) en el eje (z ). Calcule el total (D ) – flujo, ( Phi_D ) a través del área.
Considere un área elemental (dxdy ) en ( (x, , y, , 0 )). Su distancia de (Q ) es ((a ^ 2 + x ^ 2 + y ^ 2) ^ {1/2} ) por lo que la magnitud del campo (D ) – es ( frac {Q} {4 pi} cdot frac {1} {a ^ 2 + x ^ 2 + y ^ 2} ). El producto escalar de esto con el área es ( frac {Q} {4 pi} cdot frac {1} {a ^ 2 + x ^ 2 + y ^ 2} cdot cos theta dxdy, texto {y} cos theta = frac {a} {(a ^ 2 + x ^ 2 + y ^ 2) ^ {1/2}} ). La integral de superficie de ( textbf {D} ) en toda el área es
[ label {1.8.1} iint D cdot dA = frac {Qa } { pi} int_0 ^ a int_0 ^ a frac {dxdy} {(a ^ 2 + x ^ 2 + y ^ 2) ^ {3/2}}. ]
[19459001 ] Ahora todo lo que tenemos que hacer es la integral agradable y fácil. Sea (x = sqrt {a ^ 2 + y ^ 2} tan ψ ) y la integral interna ( int_0 ^ a frac {dx} {(a ^ 2 + x ^ 2 + y ^ 2) ^ {3/2}} ) reduce, después de un poco de álgebra modesta, a ( frac {a} {(a ^ 2 + y ^ 2) sqrt {2a ^ 2 + y ^ 2}} ). Por lo tanto, ahora tenemos
[ label {1.8.2} iint D cdot dA = frac {Qa ^ 2} { pi} int_0 ^ a frac { dy} {(a ^ 2 + y ^ 2) sqrt {2a ^ 2 + y ^ 2}}. ]
Con la sustitución adicional (a ^ 2 + y ^ 2 = a ^ 2 sec omega ) esto reduce, después de un álgebra más cuidadoso, a
[ iint D cdot dA = frac {Q} {6} . label {1.8.3} ]
Se pueden encontrar dos ejemplos adicionales de cálculo de integrales de superficie en la Sección 5.6, de la sección Mecánica celeste de estas notas. Estos tratan con campos gravitacionales, pero son esencialmente lo mismo que el caso electrostático; simplemente sustituya (Q ) por m y – 1 / (4 ( pi epsilon )) por (G ).
Insto a los lectores a que pasen por el dolor y el álgebra y la trigonometría de estos tres ejemplos para que puedan apreciar aún más, en la siguiente sección, el poder de Gauss teorema.