Una carga puntual (Q ) está en el centro de una esfera de radio (r ). Calcule el flujo (D ) a través de la esfera. Fácil. La magnitud de (D ) a una distancia (a ) es (Q / (4 ( pi r ^ 2) ) y el área de la superficie de la esfera es 4 ( pi ) r 2 . Por lo tanto, el flujo es solo (Q ). Observe que esto es independiente de (r ); si duplica (r ), el área es cuatro veces genial, pero (D ) es solo una cuarta parte de lo que era, por lo que el flujo total sigue siendo el mismo. Probablemente estará de acuerdo en que si la carga está rodeada por una forma como se muestra en la Figura (I ). 8 , que se compone de porciones de esferas de diferentes radios, el flujo (D ) a través de la superficie sigue siendo solo (Q ). Y puede distorsionar la superficie tanto como desee, o puede considerar cualquier la superficie estará compuesta por un número infinito de tapas esféricas infinitesimales, y puede colocar la carga en cualquier lugar que desee dentro de la superficie, o de hecho puede colocar tantas cargas dentro como desee; no ha cambiado el componente normal total de el flujo, que todavía es solo (Q ). Este es el teorema de Gauss, que es una desventaja secuencia de la naturaleza del cuadrado inverso de la ley de Coulomb.
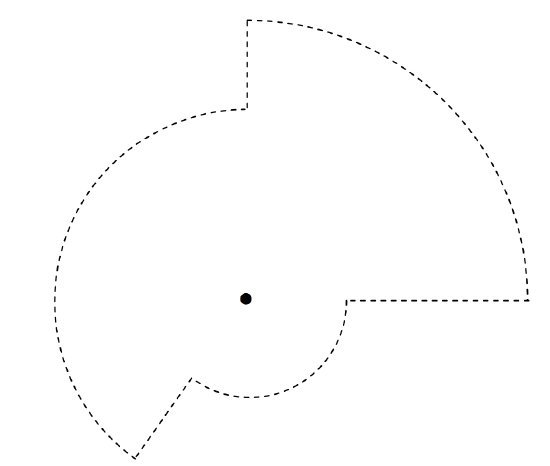
( text {FIGURE I.8} )
Definición: Teorema de Gauss
El componente normal total del flujo (D ) a través de cualquier superficie cerrada es igual a la carga encerrada por esa superficie.
Una barra larga lleva una carga de ( lambda ) por unidad de longitud. Construya a su alrededor una superficie cilíndrica de radio (r ) y longitud (l ). La carga incluida es (l lambda ), y el campo se dirige radialmente hacia afuera, pasando solo a través de la superficie curva del cilindro. El flujo (D ) – a través del cilindro es (l lambda ) y el área de la superficie curva es 2 ( pi rl ), entonces (D = l lambda / (2 pi rl ) ) y, por lo tanto, (E = lambda / (2 pi epsilon r) ).
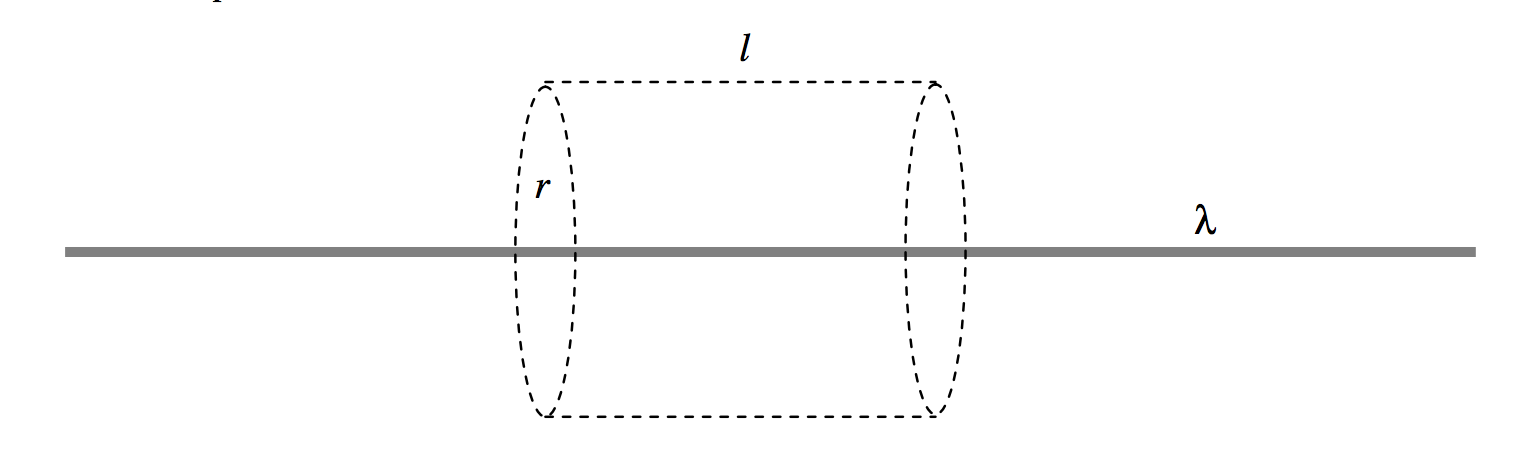
( text {FIGURA I.9} )
Una placa plana lleva una carga de ( sigma ) por unidad de área. Construya a su alrededor una superficie cilíndrica de área de sección transversal (A ). La carga encerrada por el cilindro es (A sigma ), por lo que este es el flujo (D ) a través del cilindro. Todo pasa por los dos extremos del cilindro, que tienen un área total 2 (A ), y por lo tanto (D ) = ( sigma ) / 2 y (E = sigma ) / ( 2 ( epsilon )).
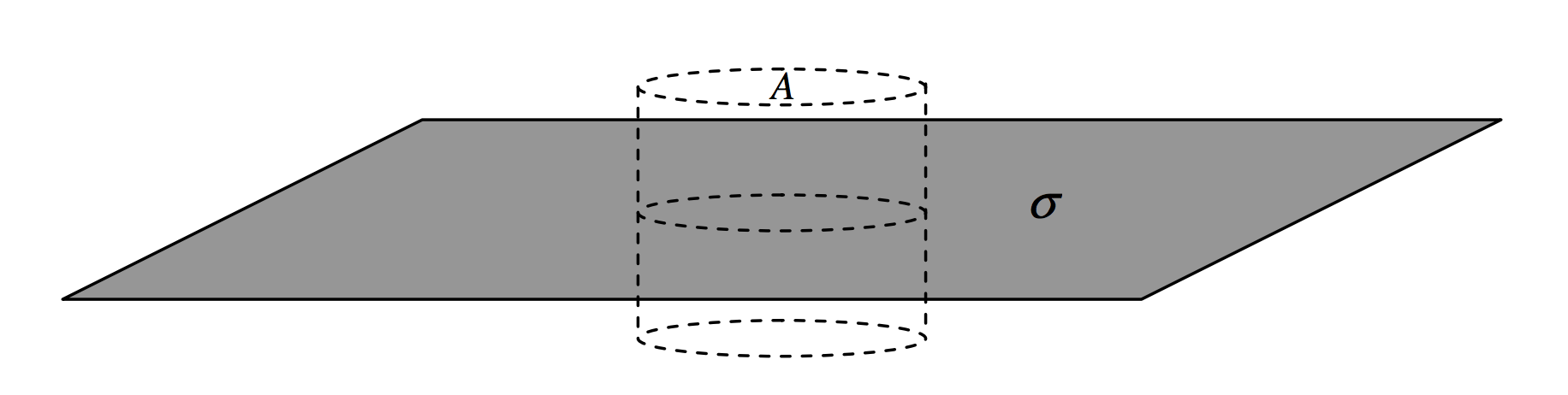
( text {FIGURA I.10} )
Una carcasa esférica hueca de radio a lleva una carga (Q ). Construya dos superficies esféricas gaussianas, una de radio menor que (a ) y la otra de radio (r> a ). La más pequeña de estas dos superficies no tiene carga en su interior; por lo tanto, el flujo a través de él es cero, por lo que (E ) es cero. La carga a través de la esfera más grande es (Q ) y su área es 4 ( pi r ^ 2 ). Por lo tanto, (D = Q / (4 pi r ^ 2) text {y} E = Q / (4 pi epsilon r ^ 2) ). (Vale la pena ir al Capítulo 5 de Mecánica celeste, subsección 5.4.8, para ver la derivación del cálculo, de modo que puedas apreciar aún más el teorema de Gauss.)
Una carga puntual (Q ) está en el medio de un cilindro de radio (a ) y longitud (2l ). Calcule el flujo a través del cilindro.
Una barra infinita se carga con ( lambda ) coulombs por unidad de longitud. Pasa centralmente a través de una superficie esférica de radio (a ). Calcule el flujo a través de la superficie esférica.
Estos problemas los resuelve el cálculo en la sección 5.6 de Mecánica celeste, y proporciona buenos ejemplos de cómo hacer integrales de superficie, y le recomiendo que los resuelva. Sin embargo, es obvio por el teorema de Gauss que las respuestas son solo (Q ) y (2a lambda ) respectivamente.
Una carga puntual (Q ) está en el medio de un cubo del lado (2a ). El flujo a través del cubo es, según el teorema de Gauss, (Q ), y el flujo a través de una cara es (Q ) / 6. Espero que hayas disfrutado haciendo este cálculo en la sección 1.8.