El circuito se muestra en la Figura X.11 y, una vez más, es importante tener cuidado con los signos.
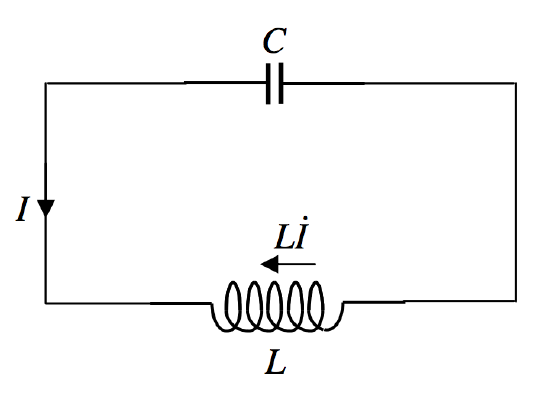
( text {FIGURE X.11} )
If (+ Q ) es la carga en la placa izquierda de la condensador en algún momento (y (- Q ) la carga en la placa de la derecha) la corriente (I ) en la dirección indicada es (- dot Q ) y la diferencia de potencial entre las placas es ( Q / C ). El EMF posterior está en la dirección que se muestra, y tenemos
[ label {10.13.1} frac {Q} {C} -L dot I = 0, ]
[19459028 ] o
[ label {10.13.2} frac {Q} {C} + L ddot Q = 0. ]
Esto se puede escribir
[19459028 ] [ label {10.13.3} ddot Q = – frac {Q} {LC}, ]
que es un movimiento armónico simple de período (2 pi sqrt {LC} ) (verifique que esto tenga dimensiones de tiempo). De este modo, la energía se desplaza de un lado a otro entre el almacenamiento como carga en el condensador y el almacenamiento como corriente en el inductor.
Si hay resistencia en el circuito, el movimiento oscilatorio se amortiguará, la carga y la corriente eventualmente se acercarán a cero. Pero, incluso si no hay resistencia, la oscilación no continúa para siempre. Si bien los detalles están más allá del alcance de este capítulo, al tratarse más fácilmente en una discusión sobre la radiación electromagnética, los cambios periódicos en la carga en el condensador y la corriente en el inductor, dan como resultado un campo electromagnético oscilante alrededor del circuito, y en la generación de una onda electromagnética, que transporta energía a una velocidad de ( sqrt {1 / ( mu_0 epsilon_0)} ). Verifique que tenga las dimensiones de velocidad y que tenga el valor (2.998 times 10 ^ 8 text {m s} ^ {−1} ). El movimiento en el circuito se amortigua como si hubiera una resistencia de ( sqrt { mu_0 / epsilon_0} = c mu_0 = 1 / (c epsilon_0) ) en el circuito. Verifique que tenga las dimensiones de resistencia y que tenga un valor de (376.7 Omega ). Esta resistencia efectiva se llama impedancia del espacio libre .