En la sección y la siguiente, se supone que el lector tiene cierta experiencia en la solución de ecuaciones diferenciales. Cuando lleguemos a una ecuación diferencial, no entraré en la mecánica de cómo resolverla, simplemente escribiré la solución de la ecuación que sigue inmediatamente, sin explicación. No se supone que un lector pueda resolver de inmediato la ecuación es su cabeza, pero podría hacerlo si le dan media hora en una habitación tranquila. Aquellos sin experiencia en ecuaciones diferenciales tendrán que tomar las soluciones dadas en confianza.
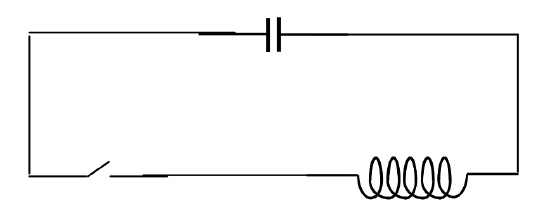
Un condensador cargado de capacitancia (C ) está conectado en serie con un interruptor y un inductor de inductancia (L ). El interruptor está cerrado y la carga fluye fuera del condensador y, por lo tanto, una corriente fluye a través del inductor. Por lo tanto, mientras el campo eléctrico en el condensador disminuye, el campo magnético en el inductor crece y se induce una fuerza electromotriz inversa (EMF) en el inductor. Deje que (Q ) sea la carga en el condensador en algún momento. La corriente (I ) que fluye desde la placa positiva es igual a (- dot Q ). La diferencia de potencial a través del condensador es (Q / C ) y el EMF posterior a través del inductor es (L dot I = -L ddot Q ). La caída potencial alrededor de todo el circuito es cero, por lo que (Q / C = -L ddot Q ). La carga en el condensador se rige por la ecuación diferencial
[ label {10.14.1} ddot Q = – frac {Q} {LC}, ]
que es un movimiento armónico simple con ( omega_0 = 1 / sqrt {LC} ). Debe verificar que tenga dimensiones ( text {T} ^ {- 1} ).
Si hay una resistencia de resistencia (R ) en el circuito, mientras una corriente fluye a través de la resistencia hay
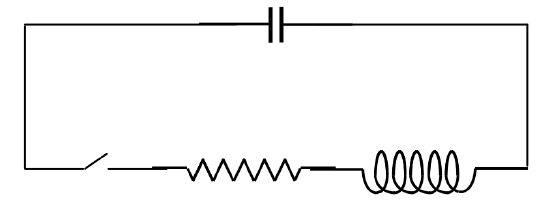
una caída potencial (RI = -R dot Q ) a través de él, y la ecuación diferencial que rige la carga en el condensador es entonces
[ label {10.14.2} LC ddot Q + RC dot Q + Q = 0. ]
Esto es amortiguado movimiento oscilatorio, la condición para la amortiguación crítica es (R ^ 2 = 4L / C ). De hecho, no es necesario tener una resistencia física en el circuito. Incluso si el condensador y el inductor estuvieran conectados por cables superconductores de resistencia cero, mientras la carga en el circuito se inclina entre el capacitor y el inductor, irradiará energía electromagnética al espacio y, por lo tanto, perderá energía. El efecto es como si hubiera una resistencia en el circuito.
Aquellos familiarizados con las ecuaciones diferenciales reconocerán que la naturaleza de la solución dependerá de si la resistencia es mayor, menor o igual que (2 sqrt { frac {L} {C}} ). Puede usar la tabla de dimensiones en Capítulo 11 para verificar que ( sqrt { frac {L} {C}} ) es dimensionalmente similar a la resistencia.
Si la resistencia es menor que (2 sqrt { frac {L} {C}} ) la carga en el condensador variará con el tiempo como [19459004 ]
[ label {10.14.3} Q = Ke ^ {- gamma t / 2} sin ( omega ^ prime t + alpha), ]
donde ( label {10.14.4} gamma = R / L ) y
[ omega ^ prime = sqrt { dfrac {1} {LC} – dfrac {R ^ 2} {4L ^ 2}}, ]
Esta es una función seno cuya amplitud disminuye exponencialmente con el tiempo. Las constantes (K ) y ( alpha ) son constantes arbitrarias de integración, que dependen de las condiciones iniciales. Si las condiciones iniciales son tales que, en el momento (t = 0 ), (Q = Q_0 ) y ( dot {Q} = I = 0 ), la ecuación ref {10.14.3} se convierte en , después de un poco de álgebra y trigonometría
[ label {10.14.5} Q = Q_0 e ^ {- gamma t / 2} left ( dfrac { gamma} {2 omega ^ prime} sin omega ^ prime t + cos omega ^ prime t. right). ]
Esta es una función seno cuya amplitud disminuye exponencialmente con el tiempo.
Si la resistencia es mayor que (2 sqrt { frac {L} {C}} ) la carga en el condensador variará con el tiempo como [19459004 ]
[ label {10.14.6} Q = Ae ^ {- lambda_1 t} + Be ^ {- lambda_2 t}, ]
donde
[ label {10.14.7} lambda_1 = dfrac {R} {2L} – sqrt { dfrac {R ^ 2} {4L ^ 2} – dfrac {1} {LC}}, quad lambda_2 = frac {R} {2L} + sqrt { dfrac {R ^ 2} {4L ^ 2} – frac {1} {LC}} ]
Aquí, y (A text {y} B ) son constantes arbitrarias de integración, que dependen de las condiciones iniciales. Si las condiciones iniciales son tales que, en el momento 0, (Q = Q_0 text {y} dot Q = I = 0 ), la ecuación ref {10.14.6} se convierte en
[ label {10.14.8} Q = frac {Q_0} { lambda_2 – lambda_1} left ( lambda_2 e ^ {- lambda_1t} – lambda_1 e ^ {- lambda_2 t} derecha). ]
Así, con estas condiciones iniciales, (Q ) disminuye monotónicamente, sin oscilación, a cero como (t → infty ).
Si la resistencia es igual a (2 sqrt { frac {L} {C}} ) la carga en el condensador variará con el tiempo como [19459004 ]
[ label {10.14.9} Q = Ke ^ {- frac {Rt} {2L}} (1 + en). ]
Si las condiciones iniciales son tales que, en el momento 0, (Q = Q_0 text {y} dot Q = I = 0 ), la ecuación ref {10.14.9} se convierte en
[ label {10.14.10} Q = Q_0e ^ {- frac {Rt} {2L}} left (1+ frac {Rt} {2L} right), ]
que disminuye monotónicamente a cero como (t → infty, text {alcance} frac {1} {2} Q_0 text {at} t = 3. 3567 R / L ).