Ahora describimos cómo la teoría cinética molecular de los gases explica algunas de las relaciones importantes que hemos discutido anteriormente.
Difusión y efusión
Como has aprendido, las moléculas de un gas no son estacionarias, sino que están en movimiento constante y aleatorio. Si alguien abre una botella de perfume en la habitación de al lado, por ejemplo, es probable que se dé cuenta pronto. Su sentido del olfato depende de que las moléculas de la sustancia aromática entren en contacto con células olfativas especializadas en sus fosas nasales, que contienen receptores específicos (moléculas de proteínas) que reconocen la sustancia. ¿Cómo llegan las moléculas responsables del aroma del frasco de perfume a la nariz? Puede pensar que son arrastrados por corrientes de aire, pero, de hecho, las moléculas pueden moverse de un lugar a otro incluso en un entorno sin corrientes de aire.
La difusión es la mezcla gradual de gases debido al movimiento de sus partículas componentes, incluso en ausencia de agitación mecánica como la agitación. El resultado es una mezcla de gases con composición uniforme. La difusión también es una propiedad de las partículas en líquidos y soluciones líquidas y, en menor medida, de sólidos y soluciones sólidas. El proceso relacionado, derrame , es el escape de moléculas gaseosas a través de un pequeño agujero (generalmente microscópico), como un agujero en un globo, hacia un espacio evacuado.
El fenómeno del derrame se conocía desde hace miles de años, pero no fue hasta principios del siglo XIX que los experimentos cuantitativos relacionaron la tasa de derrame con las propiedades moleculares. La tasa de derrame de una sustancia gaseosa es inversamente proporcional a la raíz cuadrada de su masa molar. Esta relación se conoce como Ley de Graham , después del químico escocés Thomas Graham (1805-1869). La relación de las tasas de derrame de dos gases es la raíz cuadrada de la relación inversa de sus masas molares :
[ dfrac { text {tasa de efusión A}} { text {tasa de efusión B}} = sqrt { dfrac {M_B} {M_A}} label {10.8.1} ]

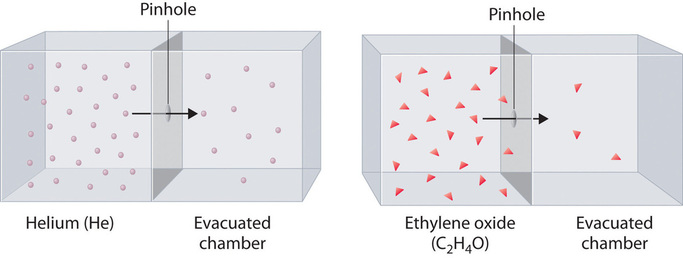
Tasas de difusión o efusión
La ley de Graham es una relación empírica que establece que la relación de las tasas de difusión o efusión de dos gases es la raíz cuadrada de la relación inversa de sus masas molares. La relación se basa en el postulado de que todos los gases a la misma temperatura tienen la misma energía cinética promedio. Podemos escribir la expresión para la energía cinética promedio de dos gases con diferentes masas molares:
[KE = dfrac {1} {2} dfrac {M _ { rm A}} {N_A} v _ { rm rms, A} ^ 2 = dfrac {1} {2} dfrac { M _ { rm B}} {N_A} v _ { rm rms, B} ^ 2 label {10.8.2} ]
Multiplicando ambos lados por 2 y reorganizando da
[ dfrac {v _ { rm rms, B} ^ 2} {v _ { rm rms, A} ^ 2} = dfrac {M _ { rm A}} {M _ { rm B}} label {10.8.3} ]
Tomando la raíz cuadrada de ambos lados da
[ dfrac {v _ { rm rms, B}} {v _ { rm rms, A}} = sqrt { dfrac {M _ { rm A}} {M _ { rm B}}} label {10.8.4} ]
Por lo tanto, la velocidad a la que una molécula, o un mol de moléculas, se difunde o efunde está directamente relacionada con la velocidad a la que se mueve. La ecuación ( ref {10.8.4} ) muestra que la ley de Graham es una consecuencia directa del hecho de que las moléculas gaseosas a la misma temperatura tienen la misma energía cinética promedio.
Típicamente, las moléculas gaseosas tienen una velocidad de cientos de metros por segundo (cientos de millas por hora). El efecto de la masa molar en estas velocidades es dramático, como se ilustra en la Figura ( PageIndex {3} ) para algunos gases comunes. Debido a que todos los gases tienen la misma energía cinética promedio, de acuerdo con la distribución de Boltzmann , las moléculas con masas más bajas, como el hidrógeno y el helio, tienen una distribución de velocidades más amplia.

Los gases más ligeros tienen una distribución más amplia de velocidades y las velocidades medias más altas.
Las moléculas de gas no se difunden casi tan rápido como podrían sugerir velocidades muy altas. Si las moléculas realmente se movieran a través de una habitación a cientos de millas por hora, detectaríamos los olores más rápido de lo que escuchamos el sonido. En cambio, nos puede tomar varios minutos detectar un aroma porque las moléculas viajan en un medio con otras moléculas de gas. Debido a que las moléculas de gas chocan tan a menudo como 10 10 veces por segundo, cambiando la dirección y la velocidad con cada colisión, no se difunden a través de una habitación en línea recta, como se ilustra esquemáticamente en la Figura ( PageIndex {4 } ).
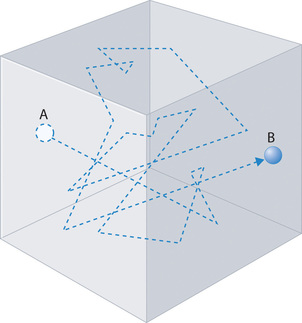
La distancia promedio recorrida por una molécula entre colisiones es la ruta libre media . Cuanto más denso es el gas, más corto es el camino libre medio; a la inversa, a medida que disminuye la densidad, el camino libre medio se alarga porque las colisiones ocurren con menos frecuencia. A 1 atm de presión y 25 ° C, por ejemplo, una molécula de oxígeno o nitrógeno en la atmósfera viaja solo alrededor de 6.0 × 10 −8 m (60 nm) entre colisiones. En la atmósfera superior a unos 100 km de altitud, donde la densidad del gas es mucho más baja, la trayectoria libre media es de unos 10 cm; en el espacio entre galaxias, puede ser tan largo como 1 × 10 10 m (aproximadamente 6 millones de millas).
La teoría cinética molecular de los gases demuestra cómo una teoría exitosa puede explicar las relaciones empíricas (leyes) observadas previamente de una manera intuitivamente satisfactoria. Desafortunadamente, los gases reales que encontramos no son “ideales”, aunque su comportamiento generalmente se aproxima al de un gas ideal.
Resumen
- La teoría cinética molecular de los gases proporciona una explicación molecular de las observaciones que condujeron al desarrollo de la ley de los gases ideales.
- Energía cinética promedio: [ overline {e_K} = dfrac {1} {2} m {u _ { rm rms}} ^ 2 = dfrac {3} {2} dfrac {R} {N_A} T, ]
- Velocidad cuadrática media raíz: [u _ { rm rms} = sqrt { dfrac {u_1 ^ 2 + u_2 ^ 2 + cdots u_N ^ 2} {N}}, ]
- Teoría cinética molecular de los gases : [u _ { rm rms} = sqrt { dfrac {3RT} {M}}. ]
- Ley de Graham para el derrame: [ dfrac {v _ { rm rms, B}} {v _ { rm rms, A}} = sqrt { dfrac {M _ { rm A }} {M _ { rm B}}} ]
La difusión es la mezcla gradual de gases para formar una muestra de composición uniforme incluso en ausencia de agitación mecánica. En contraste, derrame es el escape de un gas desde un contenedor a través de una pequeña abertura hacia un espacio evacuado. La tasa de derrame de un gas es inversamente proporcional a la raíz cuadrada de su masa molar ( Ley de Graham ), una relación que se aproxima mucho a la tasa de difusión. Como resultado, los gases ligeros tienden a difundirse y derramarse mucho más rápidamente que los gases más pesados. La ruta libre media de una molécula es la distancia promedio que viaja entre colisiones.