Saltar al contenido
atomos

10.E: Gases (ejercicios)

                 

 

 

 

 

 

 

 

 

Plantilla: PrintMe

 

Estos son ejercicios de tarea para acompañar el Mapa de texto creado para “Química: la ciencia central” por Brown et al. Se pueden encontrar bancos de preguntas de química general complementaria para otros mapas de texto y se puede acceder aquí . Además de estas preguntas disponibles públicamente, el acceso al banco privado de problemas para su uso en exámenes y tareas está disponible para los profesores solo de manera individual; comuníquese con Delmar Larsen para obtener una cuenta con permiso de acceso.

 

Tabla de contenidos

10.1: Características de los gases

 

 

Problemas conceptuales

 

 

Q10.1.1

 

Explica las diferencias entre las propiedades microscópicas y macroscópicas de la materia. ¿Es el punto de ebullición de un compuesto una propiedad microscópica o macroscópica? ¿masa molecular? ¿Por qué?

 

Q10.1.2

 

¿Cómo influyen las propiedades microscópicas de la materia en las propiedades macroscópicas? ¿Puedes relacionar la masa molecular con el punto de ebullición? ¿Por qué o por qué no?

 

Q10.1.3

 

Para una sustancia que tiene fases gaseosa, líquida y sólida, organice estas fases en orden creciente de densidad.

 

         

  1. fuerza de las interacciones intermoleculares.

    2.      

  2. compresibilidad.

    3.      

  3. movimiento molecular.

    4.      

  4. orden en la disposición de las moléculas o átomos.

    5.  

 

 

 

Q10.1.4

 

¿Qué elementos de la tabla periódica existen como gases a temperatura y presión ambiente? De estos, ¿cuáles son las moléculas diatómicas y cuáles son monoatómicas? ¿Qué elementos son líquidos a temperatura y presión ambiente? ¿Qué porción de la tabla periódica contiene elementos cuyos hidruros binarios son gases más probables a temperatura ambiente?

 

 

10.2: Presión

 

 

Q10.2.1

 

 

¿Qué cuatro cantidades deben conocerse para describir completamente una muestra de un gas? ¿Qué unidades se usan comúnmente para cada cantidad?

 

Q10.2.2

 

Si la fuerza aplicada es constante, ¿cómo cambia la presión ejercida por un objeto a medida que disminuye el área sobre la cual se ejerce la fuerza? En el mundo real, ¿cómo se aplica esta relación a la facilidad de conducir un clavo pequeño versus un clavo grande?

 

 

Q10.2.3

 

A medida que aumenta la fuerza en un área fija, ¿aumenta o disminuye la presión? Con esto en mente, ¿esperarías que una persona pesada necesite raquetas de nieve más pequeñas o más grandes que una persona más ligera? Explique.

 

Q10.2.4

 

¿Qué queremos decir con presión barométrica ? Es la presión barométrica en la cumbre del monte. ¿Más lluvioso mayor o menor que la presión en Miami, Florida? ¿Por qué?

 

Q10.2.5

 

¿Cuál tiene la presión barométrica más alta: una cueva en el Himalaya, una mina en Sudáfrica o una casa de playa en Florida? ¿Cuál tiene el más bajo?

 

Q10.2.6

 

Marte tiene una presión barométrica promedio de 0.007 atm. ¿Sería más fácil o más difícil beber líquido de una pajita en Marte que en la Tierra? Explica tu respuesta.

 

Q10.2.7

 

¿La presión ejercida por una masa de 1.0 kg en un área de 2.0 m 2 es mayor o menor que la presión ejercida por una masa de 1.0 kg en un área de 1.0 m 2 ? ¿Cuál es la diferencia, si la hay, entre la presión de la atmósfera ejercida sobre un pistón de 1.0 m 2 y un pistón de 2.0 m 2 ?

 

Q10.2.8

 

Si usara agua en un barómetro en lugar de mercurio, ¿cuál sería la principal diferencia en el instrumento?

 

 

Problemas numéricos

 

 

Q10.2.9

 

Calcule la presión en pascales y en atmósferas ejercidas por un cartón de leche que pesa 1.5 kg y tiene una base de 7.0 cm × 7.0 cm. Si el cartón estuviera acostado de lado (altura = 25 cm), ¿ejercería más o menos presión? Explica tu razonamiento.

 

Q10.2.10

 

Si la presión barométrica al nivel del mar es 1.0 × 10 5 Pa, ¿cuál es la masa de aire en kilogramos por encima de un área de su piel de 1.0 cm 2 cuando se acuesta sobre el ¿playa? Si la presión barométrica es 8.2 × 10 4 Pa en la cima de una montaña, ¿cuál es la masa de aire en kilogramos por encima de un parche de piel de 4.0 cm 2 ?

 

Q10.2.11

 

Complete la siguiente tabla:

 

 

     

         

             

             

             

             

         

     

     

         

             

             

             

             

         

         

             

             

             

             

         

         

             

             

             

             

         

     

 

cajero automático kPa mmHg torr
1,40
723
43,2

 

 

Q10.2.12

 

La ​​unidad de presión SI es el pascal, que es igual a 1 N / m 2 . Muestre cómo el producto de la masa de un objeto y la aceleración debida a la gravedad dan como resultado una fuerza que, cuando se ejerce sobre un área determinada, conduce a una presión en las unidades SI correctas. ¿Qué masa en kilogramos aplicada a un área de 1.0 cm 2 se requiere para producir una presión de

 

         

  1. 1.0 atm?

    2.      

  2. 1.0 torr?

    3.      

  3. 1 mmHg?

    4.      

  4. 1 kPa?

    5.  

 

Q10.2.13

 

If you constructed a manometer to measure gas pressures over the range 0.60–1.40 atm using the liquids given in the following table, how tall a column would you need for each liquid? The density of mercury is 13.5 g/cm 3 . Based on your results, explain why mercury is still used in barometers, despite its toxicity.

 

 

     

         

             

             

             

         

     

     

         

             

             

             

         

         

             

             

             

         

         

             

             

             

         

     

 

Liquid Density (20°C) Column Height (m)
isopropanol 0.785
coconut oil 0.924
glycerine 1.259

 

 

10.3: The Gas Laws

 

 

 

Conceptual Problems

 

 

Q10.3.1

 

Sketch a graph of the volume of a gas versus the pressure on the gas. What would the graph of V versus P look like if volume was directly proportional to pressure?

 

S10.3.1

 

 

 

 

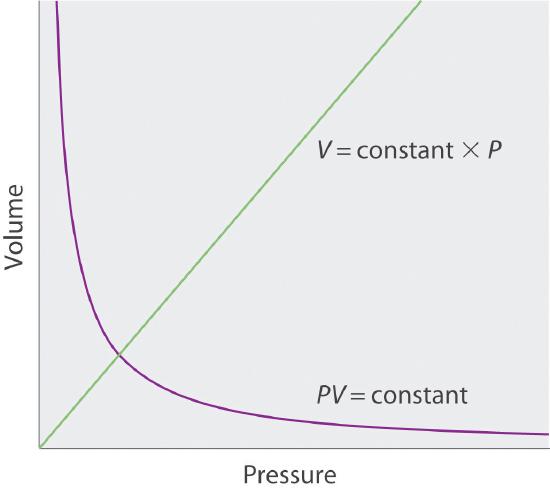
Q10.3.2

 

What properties of a gas are described by Boyle’s law, Charles’s law, and Avogadro’s law? In each law, what quantities are held constant? Why does the constant in Boyle’s law depend on the amount of gas used and the temperature at which the experiments are carried out?

 

Q10.3.3

 

Use Charles’s law to explain why cooler air sinks.

 

Q10.3.4

 

Use Boyle’s law to explain why it is dangerous to heat even a small quantity of water in a sealed container.

 

 

 

 

Numerical Problems

 

 

 

 

Q10.3.5

 

A 1.00 mol sample of gas at 25°C and 1.0 atm has an initial volume of 22.4 L. Calculate the results of each change, assuming all the other conditions remain constant.

 

         

  1. The pressure is changed to 85.7 mmHg. How many milliliters does the gas occupy?

    2.      

  2. The volume is reduced to 275 mL. What is the pressure in millimeters of mercury?

    3.      

  3. The pressure is increased to 25.3 atm. What is the temperature in degrees Celsius?

    4.      

  4. The sample is heated to 30°C. What is the volume in liters?

    5.      

  5. The sample is compressed to 1255 mL, and the pressure is increased to 2555 torr. What is the temperature of the gas in kelvins?

    6.  

 

 

 

S10.3.5

 

         

  1. 1.99 × 10 5 mL

    2.      

  2. 6.19 × 10 4 mmHg

    3.      

  3. 7270°C

    4.      

  4. 22.8 L

    5.      

  5. 51.4 K

    6.  

 

Q10.3.6

 

A 1.00 mol sample of gas is at 300 K and 4.11 atm. What is the volume of the gas under these conditions? The sample is compressed to 6.0 atm at constant temperature, giving a volume of 3.99 L. Is this result consistent with Boyle’s law?

 

 

 

10.4: The Ideal Gas Equation

 

 

 

Conceptual Problems

 

 

Q10.4.1

 

For an ideal gas, is volume directly proportional or inversely proportional to temperature? What is the volume of an ideal gas at absolute zero?

 

 

 

Q10.4.2

 

What is meant by STP? If a gas is at STP, what further information is required to completely describe the state of the gas?

 

 

 

Q10.4.3

 

For a given amount of a gas, the volume, temperature, and pressure under any one set of conditions are related to the volume, the temperature, and the pressure under any other set of conditions by the equation

[ dfrac{P_1V_1}{T_1} = dfrac{P_2V_2}{T_2} ]

 

 

Q10.4.4

 

Derive this equation from the ideal gas law. At constant temperature, this equation reduces to one of the gas laws discussed previosuly; which one? At constant pressure, this equation reduces to one of the laws discussed in Section 10.3″; which one?

 

 

 

Q10.4.5

 

Predict the effect of each change on one variable if the other variables are held constant.

 

         

  1. If the number of moles of gas increases, what is the effect on the temperature of the gas?

    2.      

  2. If the temperature of a gas decreases, what is the effect on the pressure of the gas?

    3.      

  3. If the volume of a gas increases, what is the effect on the temperature of the gas?

    4.      

  4. If the pressure of a gas increases, what is the effect on the number of moles of the gas?

    5.  

 

 

 

Q10.4.6

 

What would the ideal gas law be if the following were true?

 

         

  1. volume were proportional to pressure

    2.      

  2. temperature were proportional to amount

    3.      

  3. pressure were inversely proportional to temperature

    4.      

  4. volume were inversely proportional to temperature

    5.      

  5. both pressure and volume were inversely proportional to temperature

    6.  

 

 

 

Given the following initial and final values, what additional information is needed to solve the problem using the ideal gas law?

 

     

         

             

             

         

     

     

         

             

             

         

         

             

             

         

         

             

             

         

         

             

             

         

     

 

Given Solve for
V 1 , T 1 , T 2 , n 1 n 2
P 1 , P 2 , T 2 , n 2 n 1
T 1 , T 2 V 2
P 1 , n 1 P 2

 

 

 

 

Q10.4.7

 

Given the following information and using the ideal gas law, what equation would you use to solve the problem?

 

     

         

             

             

         

     

     

         

             

             

         

         

             

             

         

         

             

             

         

     

 

Given Solve for
P 1 , P 2 , T 1 T 2
V 1 , n 1 , n 2 V 2
T 1 , T 2 , V 1 , V 2 , n 2 n 1

 

 

 

Q10.4.8

 

Using the ideal gas law as a starting point, derive the relationship between the density of a gas and its molar mass. Which would you expect to be denser—nitrogen or oxygen? Why does radon gas accumulate in basements and mine shafts?

 

 

 

Q10.4.9

 

Use the ideal gas law to derive an equation that relates the remaining variables for a sample of an ideal gas if the following are held constant.

 

         

  1. amount and volume

    2.      

  2. pressure and amount

    3.      

  3. temperature and volume

    4.      

  4. temperature and amount

    5.      

  5. pressure and temperature

    6.  

 

 

 

S10.4.9

 

 

 

         

  1. P/T = constant

    2.      

  2. V/T = constant (Charles’ law)

    3.      

  3. P/n = constant

    4.      

  4. PV = constant (Boyle’s law)

    5.      

  5. V/n = constant (Avogadro’s law)

    6.  

 

 

 

Q10.4.10

 

Tennis balls that are made for Denver, Colorado, feel soft and do not bounce well at lower altitudes. Use the ideal gas law to explain this observation. Will a tennis ball designed to be used at sea level be harder or softer and bounce better or worse at higher altitudes?

 

 

 

 

 

     

 

 

 

 

 

Numerical Problems

 

 

Q10.4.11

 

Calculate the number of moles in each sample at STP.

 

         

  1. 1580 mL of NO 2

    2.      

  2. 847 cm 3 of HCl

    3.      

  3. 4.792 L of H 2

    4.      

  4. a 15.0 cm × 6.7 cm × 7.5 cm container of ethane

    5.  

 

S10.4.11

 

         

  1. 7.05 × 10 −2 mol

    2.      

  2. 3.78 × 10 −2 mol

    3.      

  3. 0.2138 mol

    4.      

  4. 3.4 × 10 −2 mol

    5.  

 

 

 

Q10.4.12

 

Calculate the number of moles in each sample at STP.

 

         

  1. 2200 cm 3 of CO 2

    2.      

  2. 1200 cm 3 of N 2

    3.      

  3. 3800 mL of SO 2

    4.      

  4. 13.75 L of NH 3

    5.  

 

 

 

Q10.4.13

 

Calculate the mass of each sample at STP.

 

         

  1. 36 mL of HI

    2.      

  2. 550 L of H 2 S

    3.      

  3. 1380 cm 3 of CH 4

    4.  

 

S10.4.13

 

         

  1. 0.21 g HI;

    2.      

  2. 840 g H 2 S;

    3.      

  3. 0.988 g CH 4

    4.  

 

 

 

Q10.4.14

 

Calculate the mass of each sample at STP.

 

         

  1. 3.2 L of N 2 O

    2.      

  2. 65 cm 3 of Cl 2

    3.      

  3. 3600 mL of HBr

    4.  

 

 

 

Q10.4.15

 

Calculate the volume in liters of each sample at STP.

 

         

  1. 1.68 g of Kr

    2.      

  2. 2.97 kg of propane (C 3 H 8 )

    3.      

  3. 0.643 mg of (CH 3 ) 2 O

    4.  

 

S10.4.15

 

         

  1. 0.449 L Kr

    2.      

  2. 1510 L C 3 H 8

    3.      

  3. 3.13 × 10 −4 L (CH 3 ) 2 O

    4.  

 

 

 

Q10.4.16

 

Calculate the volume in liters of each sample at STP.

 

         

  1. 3.2 g of Xe

    2.      

  2. 465 mg of CS 2

    3.      

  3. 5.34 kg of acetylene (C 2 H 2 )

    4.  

 

 

 

Q10.4.17

 

Calculate the volume of each gas at STP.

 

         

  1. 1.7 L at 28°C and 96.4 kPa

    2.      

  2. 38.0 mL at 17°C and 103.4 torr

    3.      

  3. 650 mL at −15°C and 723 mmHg

    4.  

 

 

 

Q10.4.18

 

Calculate the volume of each gas at STP.

 

         

  1. 2.30 L at 23°C and 740 mmHg

    2.      

  2. 320 mL at 13°C and 97.2 kPa

    3.      

  3. 100.5 mL at 35°C and 1.4 atm

    4.  

 

S10.4.18

 

         

  1. 1.5 L

    2.      

  2. 4.87 mL

    3.      

  3. 650 mL

    4.  

 

 

 

Q10.4.19

 

A 8.60 L tank of nitrogen gas at a pressure of 455 mmHg is connected to an empty tank with a volume of 5.35 L. What is the final pressure in the system after the valve connecting the two tanks is opened? Assume that the temperature is constant.

 

S10.4.19

 

281 mmHg

 

 

 

Q10.4.20

 

At constant temperature, what pressure in atmospheres is needed to compress 14.2 L of gas initially at 25.2 atm to a volume of 12.4 L? What pressure is needed to compress 27.8 L of gas to 20.6 L under similar conditions?

 

 

 

Q10.4.21

 

One method for preparing hydrogen gas is to pass HCl gas over hot aluminum; the other product of the reaction is AlCl 3 . If you wanted to use this reaction to fill a balloon with a volume of 28,500 L at sea level and a temperature of 78°F, what mass of aluminum would you need? What volume of HCl at STP would you need?

 

S10.4.21

 

20.9 kg Al, 5.20 × 10 4 L HCl

 

 

 

Q10.4.21

 

An 3.50 g sample of acetylene is burned in excess oxygen according to the following reaction:

 

[ce{2 C2H2(g) + 5 O2(g) → 4 CO2(g) + 2 H2O(l)}]

 

At STP, what volume of CO 2 (g) is produced?

 

 

 

Q10.4.22

 

Calculate the density of ethylene (C 2 H 4 ) under each set of conditions.

 

         

  1. 7.8 g at 0.89 atm and 26°C

    2.      

  2. 6.3 mol at 102.6 kPa and 38°C

    3.      

  3. 9.8 g at 3.1 atm and −45°C

    4.  

 

S10.4.22

 

         

  1. 1.0 g/L

    2.      

  2. 1.1 g/L

    3.      

  3. 4.6 g/L

    4.  

 

 

 

Q10.4.23

 

Determine the density of O 2 under each set of conditions.

 

         

  1. 42 g at 1.1 atm and 25°C

    2.      

  2. 0.87 mol at 820 mmHg and 45°C

    3.      

  3. 16.7 g at 2.4 atm and 67°C

    4.  

 

 

 

Q10.4.24

 

At 140°C, the pressure of a diatomic gas in a 3.0 L flask is 635 kPa. The mass of the gas is 88.7 g. What is the most likely identity of the gas?

 

 

 

Q10.4.25

 

What volume must a balloon have to hold 6.20 kg of H 2 for an ascent from sea level to an elevation of 20,320 ft, where the temperature is −37°C and the pressure is 369 mmHg?

 

 

 

Q10.4.26

 

What must be the volume of a balloon that can hold 313.0 g of helium gas and ascend from sea level to an elevation of 1.5 km, where the temperature is 10.0°C and the pressure is 635.4 mmHg?

 

S10.4.26

 

2174 L

 

 

 

Q10.4.27

 

A typical automobile tire is inflated to a pressure of 28.0 lb/in. 2 Assume that the tire is inflated when the air temperature is 20°C; the car is then driven at high speeds, which increases the temperature of the tire to 43°C. What is the pressure in the tire? If the volume of the tire had increased by 8% at the higher temperature, what would the pressure be?

 

 

 

Q10.4.28

 

The average respiratory rate for adult humans is 20 breaths per minute. If each breath has a volume of 310 mL of air at 20°C and 0.997 atm, how many moles of air does a person inhale each day? If the density of air is 1.19 kg/m 3 , what is the average molecular mass of air?

 

 

 

Q10.4.29

 

Kerosene has a self-ignition temperature of 255°C. It is a common accelerant used by arsonists, but its presence is easily detected in fire debris by a variety of methods. If a 1.0 L glass bottle containing a mixture of air and kerosene vapor at an initial pressure of 1 atm and an initial temperature of 23°C is pressurized, at what pressure would the kerosene vapor ignite?​

 

 

 

10.5: Further Applications of the Ideal-Gas Equations

 

 

Conceptual Problems

 

Q10.5.1

 

Why are so many industrially important reactions carried out in the gas phase?

 

Q10.5.2

 

The volume of gas produced during a chemical reaction can be measured by collecting the gas in an inverted container filled with water. The gas forces water out of the container, and the volume of liquid displaced is a measure of the volume of gas. What additional information must be considered to determine the number of moles of gas produced? The volume of some gases cannot be measured using this method. What property of a gas precludes the use of this method?

 

Q10.5.3

 

Equal masses of two solid compounds (A and B) are placed in separate sealed flasks filled with air at 1 atm and heated to 50°C for 10 hours. After cooling to room temperature, the pressure in the flask containing A was 1.5 atm. In contrast, the pressure in the flask containing B was 0.87 atm. Suggest an explanation for these observations. Would the masses of samples A and B still be equal after the experiment? Why or why not?

 

Numerical Problems

 

Q10.5.4

 

Balance each chemical equation and then determine the volume of the indicated reactant at STP that is required for complete reaction. Assuming complete reaction, what is the volume of the products?

 

         

  1. SO 2 (g) + O 2 (g) → SO 3 (g) given 2.4 mol of O 2

    2.      

  2. H 2 (g) + Cl 2 (g) → HCl(g) given 0.78 g of H 2

    3.      

  3. C 2 H 6 (g) + O 2 (g) → CO 2 (g) + H 2 O(g) given 1.91 mol of O 2

    4.  

 

Q10.5.5

 

During the smelting of iron, carbon reacts with oxygen to produce carbon monoxide, which then reacts with iron(III) oxide to produce iron metal and carbon dioxide. If 1.82 L of CO 2 at STP is produced,

 

         

  1. what mass of CO is consumed?

    2.      

  2. what volume of CO at STP is consumed?

    3.      

  3. how much O 2 (in liters) at STP is used?

    4.      

  4. what mass of carbon is consumed?

    5.      

  5. how much iron metal (in grams) is produced?

    6.  

 

Q10.5.6

 

Complete decomposition of a sample of potassium chlorate produced 1.34 g of potassium chloride and oxygen gas.

 

         

  1. What is the mass of KClO 3 in the original sample?

    2.      

  2. What mass of oxygen is produced?

    3.      

  3. What is the volume of oxygen produced at STP?

    4.  

 

S10.5.6

 

         

  1. 2.20 g KClO 3

    2.      

  2. 0.863 g O 2

    3.      

  3. 604 mL O 2

    4.  

 

Q10.5.7

 

The combustion of a 100.0 mg sample of an herbicide in excess oxygen produced 83.16 mL of CO 2 and 72.9 mL of H 2 O vapor at STP. A separate analysis showed that the sample contained 16.44 mg of chlorine. If the sample is known to contain only C, H, Cl, and N, determine the percent composition and the empirical formula of the herbicide.

 

Q10.5.8

 

The combustion of a 300.0 mg sample of an antidepressant in excess oxygen produced 326 mL of CO 2 and 164 mL of H 2 O vapor at STP. A separate analysis showed that the sample contained 23.28% oxygen. If the sample is known to contain only C, H, O, and N, determine the percent composition and the empirical formula of the antidepressant.

 

S10.5.8

 

Percent composition: 58.3% C, 4.93% H, 23.28% O, and 13.5% N; empirical formula: C 10 H 10 O 3 N 2

 

10.6: Gas Mixtures and Partial Pressures

 

 

Conceptual Problems

 

 

Q10.6.1

 

Dalton’s law of partial pressures makes one key assumption about the nature of the intermolecular interactions in a mixture of gases. ¿Qué es?

 

 

Q10.6.2

 

What is the relationship between the partial pressure of a gas and its mole fraction in a mixture?

 

Numerical Problems

 

 

Q10.6.3

 

What is the partial pressure of each gas if the following amounts of substances are placed in a 25.0 L container at 25°C? What is the total pressure of each mixture?

 

         

  1. 1.570 mol of CH 4 and 0.870 mol of CO 2

    2.      

  2. 2.63 g of CO and 1.24 g of NO 2

    3.      

  3. 1.78 kg of CH 3 Cl and 0.92 kg of SO 2

    4.  

 

 

Q10.6.4

 

What is the partial pressure of each gas in the following 3.0 L mixtures at 37°C as well as the total pressure?

 

         

  1. 0.128 mol of SO 2 and 0.098 mol of methane (CH 4 )

    2.      

  2. 3.40 g of acetylene (C 2 H 2 ) and 1.54 g of He

    3.      

  3. 0.267 g of NO, 4.3 g of Ar, and 0.872 g of SO 2

    4.  

 

Q10.6.5

 

In a mixture of helium, oxygen, and methane in a 2.00 L container, the partial pressures of He and O 2 are 13.6 kPa and 29.2 kPa, respectively, and the total pressure inside the container is 95.4 kPa. What is the partial pressure of methane? If the methane is ignited to initiate its combustion with oxygen and the system is then cooled to the original temperature of 30°C, what is the final pressure inside the container (in kilopascals)?

 

S10.6.5

 

52.6 kPa, 66.2 kPa

 

Q10.6.6

 

A 2.00 L flask originally contains 1.00 g of ethane (C 2 H 6 ) and 32.0 g of oxygen at 21°C. During ignition, the ethane reacts completely with oxygen to produce CO 2 and water vapor, and the temperature of the flask increases to 200°C. Determine the total pressure and the partial pressure of each gas before and after the reaction.

 

Q10.6.7

 

If a 20.0 L cylinder at 19°C is charged with 5.0 g each of sulfur dioxide and oxygen, what is the partial pressure of each gas? The sulfur dioxide is ignited in the oxygen to produce sulfur trioxide gas, and the mixture is allowed to cool to 19°C at constant pressure. What is the final volume of the cylinder? What is the partial pressure of each gas in the piston?

 

Q10.6.8

 

The highest point on the continent of Europe is Mt. Elbrus in Russia, with an elevation of 18,476 ft. The highest point on the continent of South America is Mt. Aconcagua in Argentina, with an elevation of 22,841 ft.

 

         

  1.      

    The following table shows the variation of atmospheric pressure with elevation. Use the data in the table to construct a plot of pressure versus elevation.

         

             

                 

                     

                     

                     

                 

             

             

                 

                     

                     

                     

                 

                 

                     

                     

                     

                 

                 

                     

                     

                     

                 

                 

                     

                     

                     

                 

                 

                     

                     

                     

                 

                 

                     

                     

                     

                 

                 

                     

                     

                     

                 

                 

                     

                     

                     

                 

             

         

    Elevation (km) Pressure in Summer (mmHg) Pressure in Winter (mmHg)
    0.0 760.0 760.0
    1.0 674.8 670.6
    1.5 635.4 629.6
    2.0 598.0 590.8
    3.0 528.9 519.7
    5.0 410.6 398.7
    7.0 314.9 301.6
    9.0 237.8 224.1

         

    2.      

  2. Use your graph to estimate the pressures in millimeters of mercury during the summer and the winter at the top of both mountains in both atmospheres and kilopascals.

    3.      

  3. Given that air is 20.95% O 2 by volume, what is the partial pressure of oxygen in atmospheres during the summer at each location?

    4.  

 

10.7: Kinetic-Molecular Theory

 

 

 

 

 

10.8: Molecular Effusion and Diffusion

 

 

 

Conceptual Problems

 

Q10.8.1

 

Which of the following processes represents effusion, and which represents diffusion?

 

         

  1. helium escaping from a hole in a balloon

    2.      

  2. vapor escaping from the surface of a liquid

    3.      

  3. gas escaping through a membrane

    4.  

 

 

Q10.8.2

 

Which postulate of the kinetic molecular theory of gases most readily explains the observation that a helium-filled balloon is round?

 

Q10.8.3

 

Why is it relatively easy to compress a gas? How does the compressibility of a gas compare with that of a liquid? A solid? ¿Por qué? Which of the postulates of the kinetic molecular theory of gases most readily explains these observations?

 

Q10.8.4

 

What happens to the average kinetic energy of a gas if the rms speed of its particles increases by a factor of 2? How is the rms speed different from the average speed?

 

Q10.8.5

 

Which gas—radon or helium—has a higher average kinetic energy at 100°C? Which has a higher average speed? ¿Por qué? Which postulate of the kinetic molecular theory of gases most readily supports your answer?

 

Q10.8.6

 

What is the relationship between the average speed of a gas particle and the temperature of the gas? What happens to the distribution of molecular speeds if the temperature of a gas is increased? Decreased?

 

Q10.8.7

 

Qualitatively explain the relationship between the number of collisions of gas particles with the walls of a container and the pressure of a gas. How does increasing the temperature affect the number of collisions?

 

Q10.8.8

 

What happens to the average kinetic energy of a gas at constant temperature if the

 

         

  1. volume of the gas is increased?

    2.      

  2. pressure of the gas is increased?

    3.  

 

Q10.8.9

 

What happens to the density of a gas at constant temperature if the

 

         

  1. volume of the gas is increased?

    2.      

  2. pressure of the gas is increased?

    3.  

 

Q10.8.10

 

Use the kinetic molecular theory of gases to describe how a decrease in volume produces an increase in pressure at constant temperature. Similarly, explain how a decrease in temperature leads to a decrease in volume at constant pressure.

 

Q10.8.11

 

Graham’s law is valid only if the two gases are at the same temperature. ¿Por qué?

 

Q10.8.12

 

If we lived in a helium atmosphere rather than in air, would we detect odors more or less rapidly than we do now? Explain your reasoning. Would we detect odors more or less rapidly at sea level or at high altitude? ¿Por qué?

 

 

Numerical Problems

 

Q10.8.13

 

At a given temperature, what is the ratio of the rms speed of the atoms of Ar gas to the rms speed of molecules of H 2 gas?

 

S10.8.13

 

At any temperature, the rms speed of hydrogen is 4.45 times that of argon.

 

 

Q10.8.14

 

At a given temperature, what is the ratio of the rms speed of molecules of CO gas to the rms speed of molecules of H 2 S gas?

 

Q10.8.15

 

What is the ratio of the rms speeds of argon and oxygen at any temperature? Which diffuses more rapidly?

 

Q10.8.16

 

What is the ratio of the rms speeds of Kr and NO at any temperature? Which diffuses more rapidly?

 

Q10.8.17

 

Deuterium (D) and tritium (T) are heavy isotopes of hydrogen. Tritium has an atomic mass of 3.016 amu and has a natural abundance of 0.000138%. The effusion of hydrogen gas (containing a mixture of H 2 , HD, and HT molecules) through a porous membrane can be used to obtain samples of hydrogen that are enriched in tritium. How many membrane passes are necessary to give a sample of hydrogen gas in which 1% of the hydrogen molecules are HT?

 

Q10.8.18

 

Samples of HBr gas and NH 3 gas are placed at opposite ends of a 1 m tube. If the two gases are allowed to diffuse through the tube toward one another, at what distance from each end of the tube will the gases meet and form solid NH 4 Br?

 

10.9: Real Gases: Deviations from Ideal Behavior

 

 

 

Conceptual Problems

 

Q10.9.1

 

What factors cause deviations from ideal gas behavior? Use a sketch to explain your answer based on interactions at the molecular level.

 

 

Q10.9.2

 

Explain the effect of nonzero atomic volume on the ideal gas law at high pressure. Draw a typical graph of volume versus 1/ P for an ideal gas and a real gas.

 

Q10.9.3

 

For an ideal gas, the product of pressure and volume should be constant, regardless of the pressure. Experimental data for methane, however, show that the value of PV decreases significantly over the pressure range 0 to 120 atm at 0°C. The decrease in PV over the same pressure range is much smaller at 100°C. Explain why PV decreases with increasing temperature. Why is the decrease less significant at higher temperatures.

 

Q10.9.4

 

What is the effect of intermolecular forces on the liquefaction of a gas? At constant pressure and volume, does it become easier or harder to liquefy a gas as its temperature increases? Explain your reasoning. What is the effect of increasing the pressure on the liquefaction temperature?

 

Q10.9.5

 

Describe qualitatively what a and b , the two empirical constants in the van der Waals equation, represent.

 

Q10.9.6

 

In the van der Waals equation, why is the term that corrects for volume negative and the term that corrects for pressure positive? Why is n / V squared?

 

Q10.9.7

 

Liquefaction of a gas depends strongly on two factors. What are they? As temperature is decreased, which gas will liquefy first—ammonia, methane, or carbon monoxide? ¿Por qué?

 

Q10.9.8

 

What is a cryogenic liquid? Describe three uses of cryogenic liquids.

 

Q10.9.9

 

Air consists primarily of O 2 , N 2 , Ar, Ne, Kr, and Xe. Use the concepts discussed in this chapter to propose two methods by which air can be separated into its components. Which component of air will be isolated first?

 

Q10.9.10

 

How can gas liquefaction facilitate the storage and transport of fossil fuels? What are potential drawbacks to these methods?

 

 

Numerical Problems

 

Q10.9.11

 

The van der Waals constants for xenon are a = 4.19 (L 2 ·atm)/mol 2 and b = 0.0510 L/mol. If a 0.250 mol sample of xenon in a container with a volume of 3.65 L is cooled to −90°C, what is the pressure of the sample assuming ideal gas behavior? What would be the actual pressure under these conditions?

 

 

Q10.9.12

 

The van der Waals constants for water vapor are a = 5.46 (L 2 ·atm)/mol 2 and b = 0.0305 L/mol. If a 20.0 g sample of water in a container with a volume of 5.0 L is heated to 120°C, what is the pressure of the sample assuming ideal gas behavior? What would be the actual pressure under these conditions?

 

                     

 

             

Post Views: 13