Es posible utilizar estudios cinéticos de un sistema químico, como el efecto de los cambios en las concentraciones de reactivos, para deducir eventos que ocurren a escala microscópica, como colisiones entre partículas individuales. Dichos estudios han llevado al modelo de colisión de la cinética química, que es una herramienta útil para comprender el comportamiento de las especies químicas que reaccionan. Según el modelo de colisión, una reacción química puede ocurrir solo cuando las moléculas reactivas, los átomos o los iones colisionan con más de una cierta cantidad de energía cinética y en la orientación adecuada. El modelo de colisión explica por qué, por ejemplo, la mayoría de las colisiones entre moléculas no producen una reacción química. Las moléculas de nitrógeno y oxígeno en un solo litro de aire a temperatura ambiente y 1 atm de presión chocan aproximadamente 10 30 veces por segundo. Si cada colisión produjera dos moléculas de NO, la atmósfera se habría convertido en NO y luego en NO 2 hace mucho tiempo. En cambio, en la mayoría de las colisiones, las moléculas simplemente rebotan entre sí sin reaccionar, de la misma manera que las canicas rebotan entre sí cuando chocan. El modelo de colisión también explica por qué tales reacciones químicas ocurren más rápidamente a temperaturas más altas. Por ejemplo, las velocidades de reacción de muchas reacciones que ocurren a temperatura ambiente aproximadamente se duplican con un aumento de temperatura de solo 10 ° C. En esta sección, utilizaremos el modelo de colisión para analizar esta relación entre la temperatura y las velocidades de reacción.
Energía de activación
Anteriormente, discutimos la teoría cinética molecular de los gases, que mostró que la energía cinética promedio de las partículas de un gas aumenta con el aumento de la temperatura. Debido a que la velocidad de una partícula es proporcional a la raíz cuadrada de su energía cinética, aumentar la temperatura también aumentará el número de colisiones entre moléculas por unidad de tiempo. Lo que la teoría cinética molecular de los gases no explica es por qué la velocidad de reacción de la mayoría de las reacciones se duplica aproximadamente con un aumento de temperatura de 10 ° C. Este resultado es sorprendentemente grande teniendo en cuenta que un aumento de 10 ° C en la temperatura de un gas de 300 K a 310 K aumenta la energía cinética de las partículas solo en aproximadamente un 4%, lo que lleva a un aumento en la velocidad molecular de solo aproximadamente 2% y un aumento correspondientemente pequeño en el número de colisiones bimoleculares por unidad de tiempo.
El modelo de colisión de la cinética química explica este comportamiento al introducir el concepto de energía de activación ( E a ) . Definiremos este concepto utilizando la reacción de (NO ) con ozono, que juega un papel importante en el agotamiento del ozono en la capa de ozono:
[NO (g) + O_3 (g) rightarrow NO_2 (g) + O_2 (g) label {14.5.1} ]
El aumento de la temperatura de 200 K a 350 K hace que la velocidad constante para esta reacción en particular aumente en un factor de más de 10, mientras que el aumento en la frecuencia de colisiones bimoleculares en este rango de temperatura es solo del 30%. Por lo tanto, algo más que un aumento en la velocidad de colisión debe estar afectando la velocidad de reacción.
La velocidad de reacción, no la velocidad constante, variará con la concentración. La tasa constante, sin embargo, varía con la temperatura. Fi gure La tabla ( PageIndex {1} ) muestra un gráfico de la constante de velocidad de la reacción de NO con O 3 [19459010 ] a varias temperaturas. La relación no es lineal, sino que se asemeja a las relaciones observadas en los gráficos de presión de vapor versus temperatura. En los tres casos, la forma de las gráficas resulta de una distribución de energía cinética sobre una población de partículas (electrones en el caso de la conductividad; moléculas en el caso de la presión de vapor; y moléculas, átomos o iones en el caso de la reacción tarifas). Solo una fracción de las partículas tiene suficiente energía para superar una barrera energética.
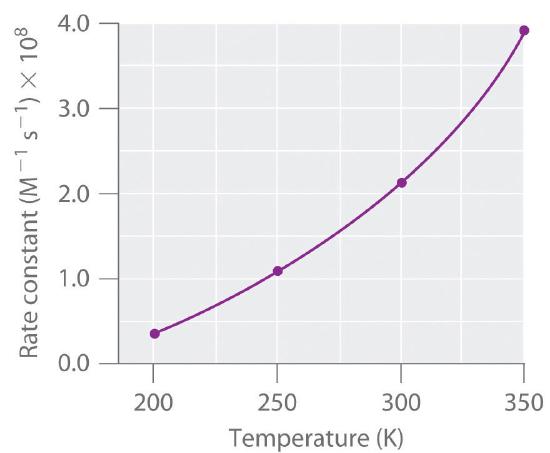
En el caso de la presión de vapor, las partículas deben superar una barrera de energía para escapar de la fase líquida a la fase gaseosa. Esta barrera corresponde a la energía de las fuerzas intermoleculares que mantienen unidas las moléculas en el líquido. En conductividad, la barrera es la brecha de energía entre las bandas llenas y vacías. En las reacciones químicas, la barrera energética corresponde a la cantidad de energía que las partículas deben tener para reaccionar cuando chocan. Este umbral de energía, llamado energía de activación, fue postulado por primera vez en 1888 por el químico sueco Svante Arrhenius (1859-1927; Premio Nobel de Química 1903). Es la cantidad mínima de energía necesaria para que ocurra una reacción. Las moléculas que reaccionan deben tener suficiente energía para vencer la repulsión electrostática, y se requiere una cantidad mínima de energía para romper los enlaces químicos para que se puedan formar nuevos. Las moléculas que chocan con menos del umbral de energía rebotan entre sí químicamente sin cambios, con solo su dirección de viaje y su velocidad alterada por la colisión. Las moléculas que pueden superar la barrera de energía pueden reaccionar y formar una disposición de átomos llamada complejo activado o estado de transición de la reacción. El complejo activado no es una reacción intermedia; no dura lo suficiente como para ser detectado fácilmente.
Cualquier fenómeno que depende de la distribución de energía térmica en una población de partículas tiene una dependencia no lineal de la temperatura.
Graficando los cambios de energía durante una reacción
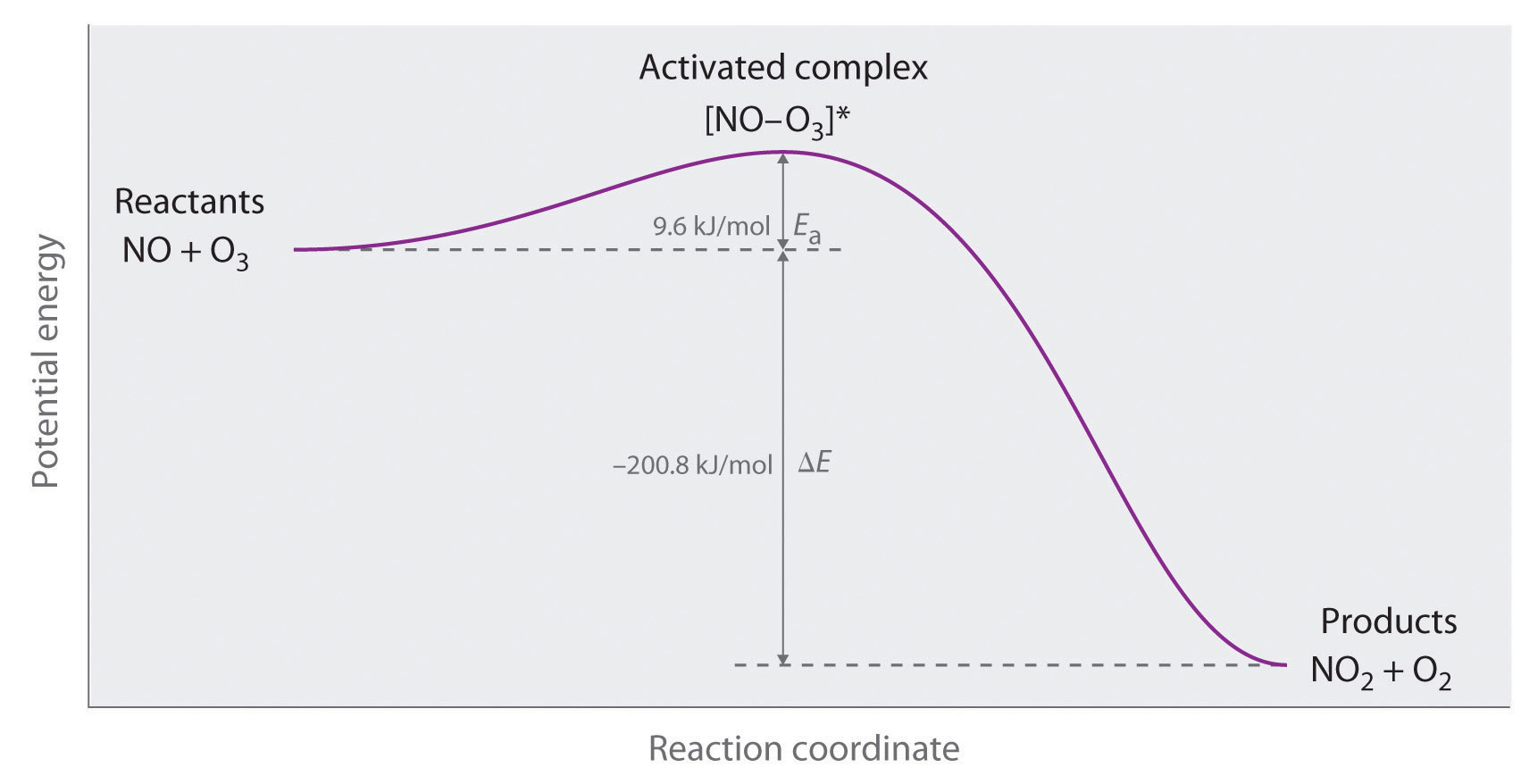
Podemos graficar la energía de una reacción trazando la energía potencial del sistema a medida que la reacción progresa. La figura ( PageIndex {2} ) muestra un gráfico para el sistema NO – O 3 , en el que el eje vertical es energía potencial y el eje horizontal es la coordenada de reacción, que indica el progreso de la reacción con el tiempo. El complejo activado se muestra entre paréntesis con un asterisco. El cambio general en la energía potencial para la reacción (Δ E ) es negativo, lo que significa que la reacción libera energía. (En este caso, Δ E es −200.8 kJ / mol.) Sin embargo, para reaccionar, las moléculas deben superar la barrera de energía para la reacción ( E a es 9.6 kJ / mol). Es decir, 9.6 kJ / mol se deben poner en el sistema como la energía de activación. Por debajo de este umbral, las partículas no tienen suficiente energía para que ocurra la reacción.
La parte (a) en Figu re ( PageIndex {3} ) ilustra la situación general en la que los productos tienen una energía potencial menor que los reactivos. En contraste, la parte (b) en Figu re ( PageIndex {3} ) ilustra el caso en el que los productos tienen una energía potencial mayor que los reactivos, por lo que la reacción general requiere un aporte de energía ; es decir, es energéticamente cuesta arriba, y Δ E > 0. Aunque los cambios de energía que resultan de una reacción pueden ser positivos, negativos o incluso cero, en todos los casos se debe superar una barrera energética antes de un La reacción puede ocurrir. Esto significa que la energía de activación siempre es positiva.
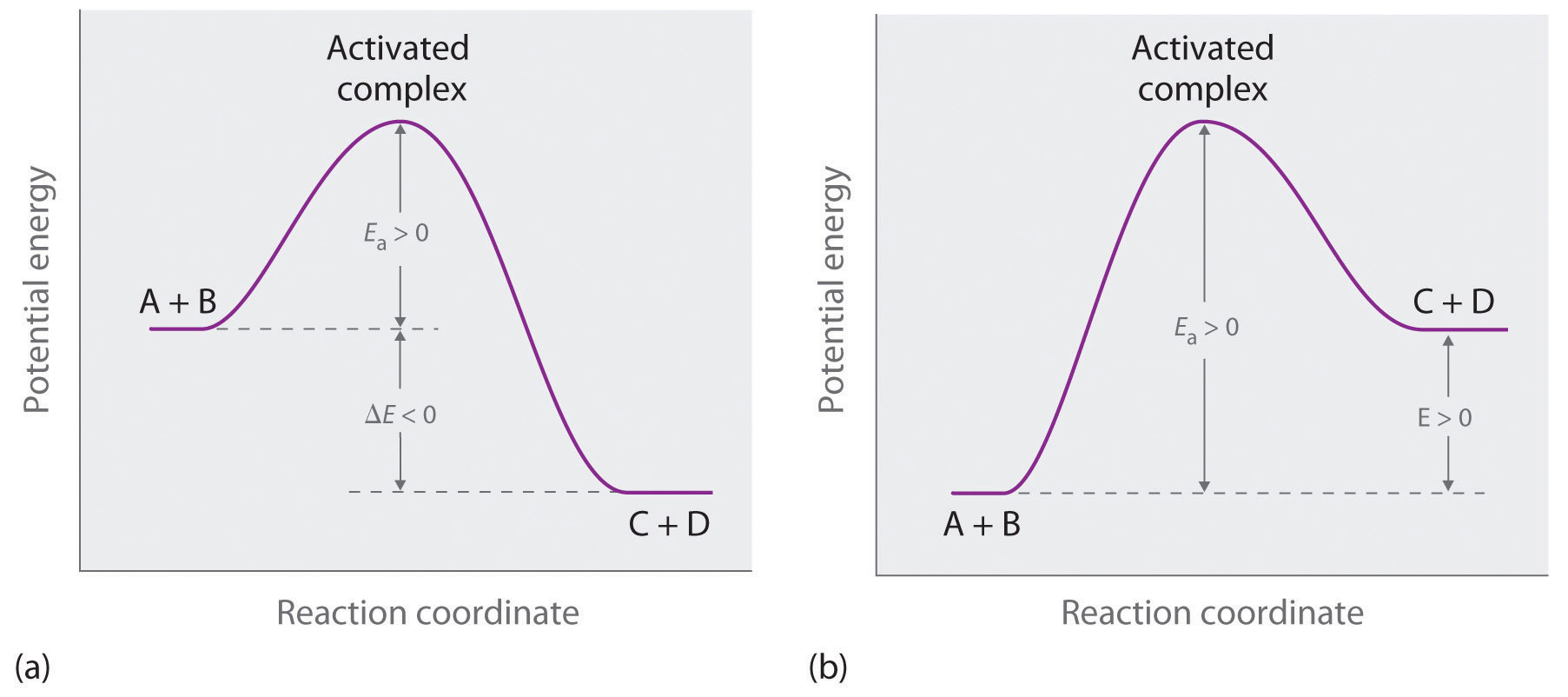
Para reacciones similares en condiciones comparables, la más pequeña E a ocurrirá más rápidamente.
Mientras que Δ E está relacionado con la tendencia de una reacción a ocurrir espontáneamente, E a nos da información sobre la velocidad de reacción y la rapidez con la que la reacción La velocidad cambia con la temperatura. Para dos reacciones similares en condiciones comparables, la reacción con la E a más pequeña ocurrirá más rápidamente.
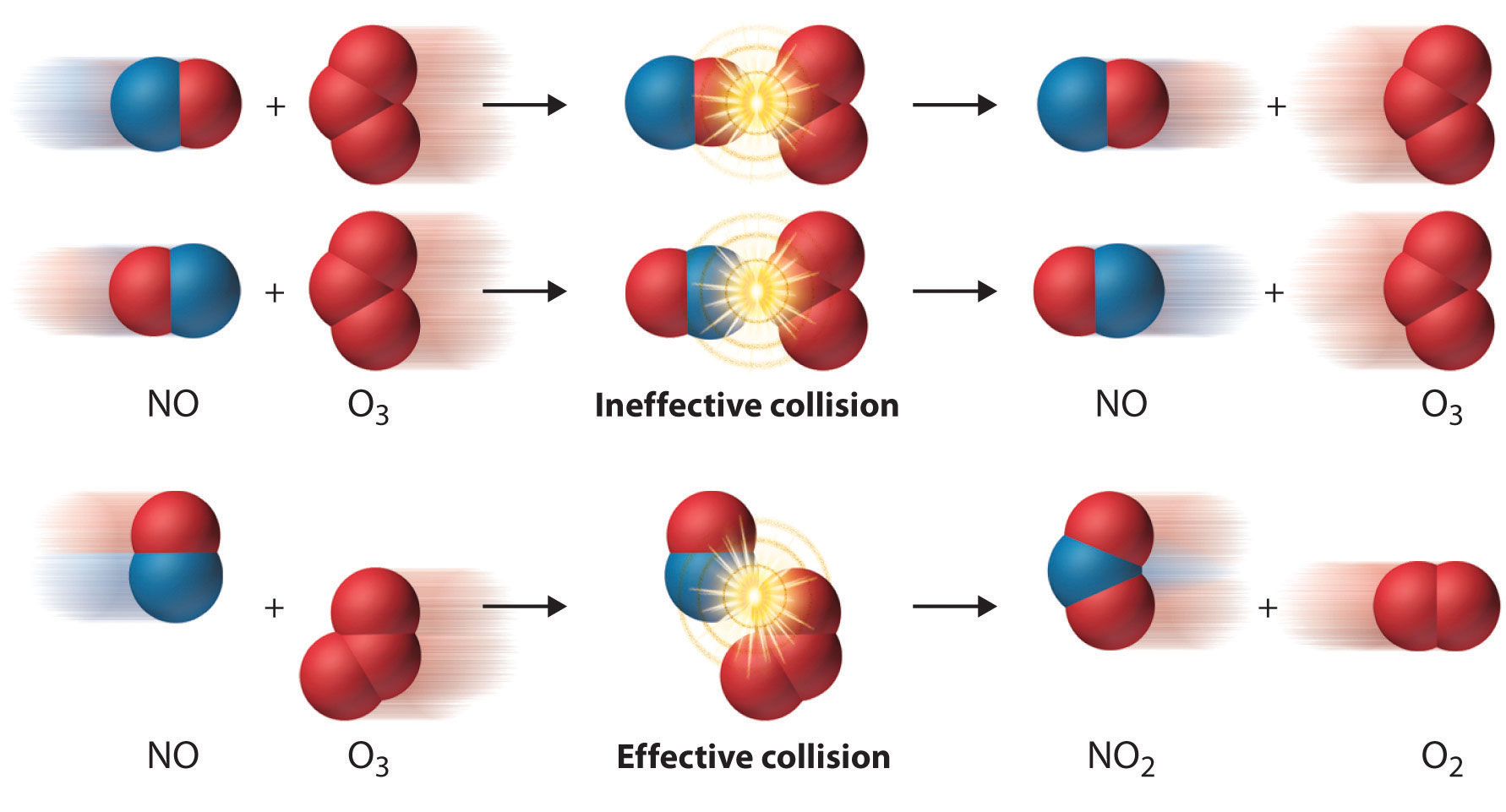
Incluso cuando la energía de las colisiones entre dos especies reactivas es mayor que E a , sin embargo, la mayoría de las colisiones no producen una reacción. La probabilidad de que ocurra una reacción depende no solo de la energía de colisión sino también de la orientación espacial de las moléculas cuando colisionan. Para que NO y O 3 produzcan NO 2 y O 2 , un átomo de oxígeno terminal de O 3 debe colisionar con el átomo de nitrógeno de NO en un ángulo que permite que O 3 transfiera un átomo de oxígeno a NO para producir NO 2 ( Figu re ( PageIndex {4} ) ) Todas las demás colisiones no producen reacción. Debido a que menos del 1% de todas las orientaciones posibles de NO y O 3 resultan en una reacción a energías cinéticas mayores que E a , la mayoría de las colisiones de NO y O 3 son improductivos. La fracción de orientaciones que dan como resultado una reacción se denomina factor estérico ( p ) y, en general, su valor puede variar de 0 (ninguna orientación de las moléculas da como resultado la reacción) a 1 (todas las orientaciones dan como resultado una reacción).
La ecuación de Arrhenius
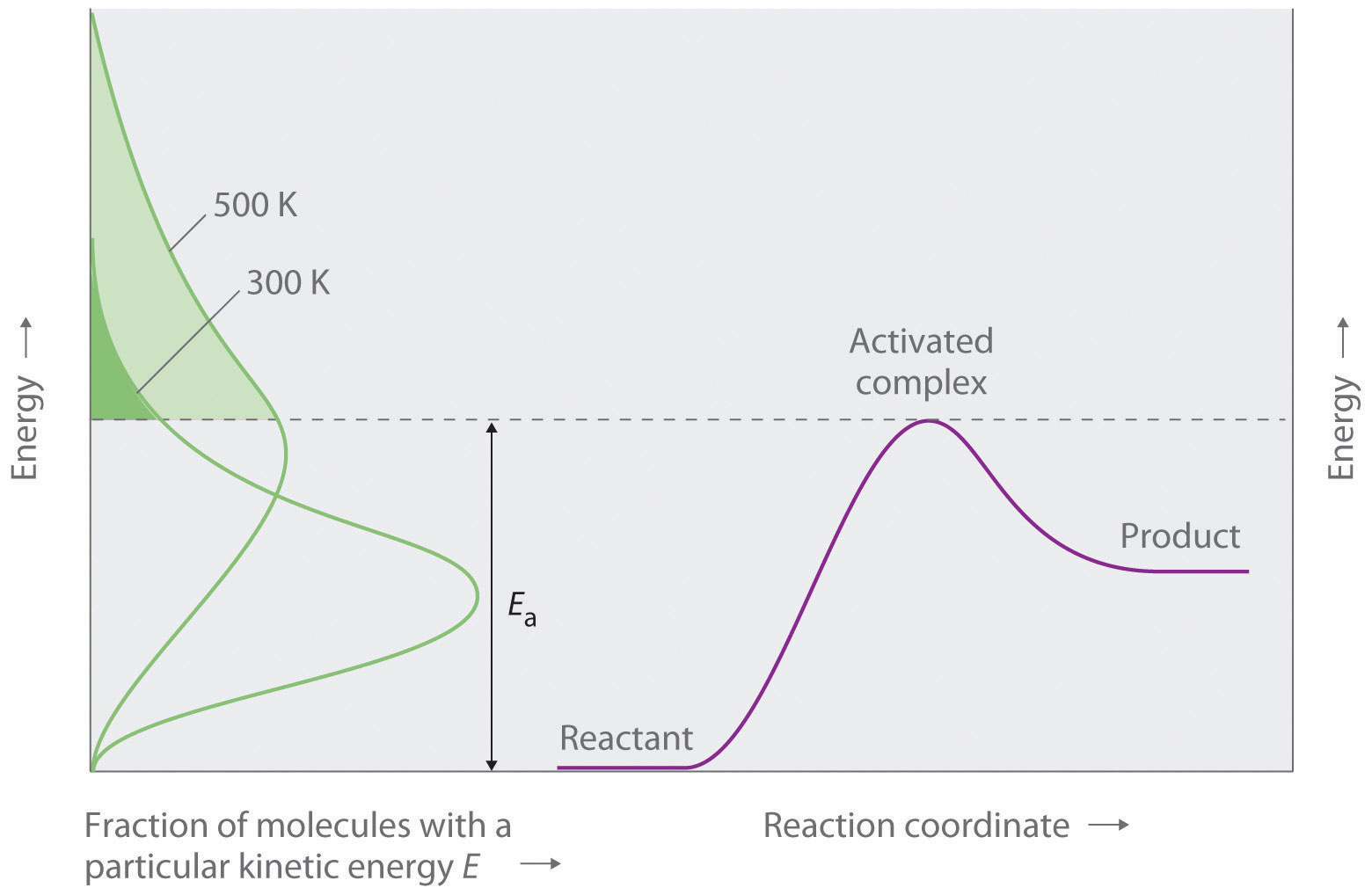
La figura 14.5.5 muestra tanto las distribuciones de energía cinética como un diagrama de energía potencial para una reacción. Las áreas sombreadas muestran que a la temperatura más baja (300 K), solo una pequeña fracción de moléculas choca con una energía cinética mayor que E a ; sin embargo, a la temperatura más alta (500 K) una fracción mucho mayor de moléculas choca con una energía cinética mayor que E a . En consecuencia, la velocidad de reacción es mucho más lenta a la temperatura más baja porque solo unas pocas moléculas chocan con suficiente energía para superar la barrera de energía potencial.
Para una reacción elemental A + B, todos los factores que afectan la velocidad de reacción se pueden resumir en una sola serie de relaciones:
tasa = (frecuencia de colisión) (factor estérico) (fracción de colisiones con E > E a )
donde
[tasa = k [A] [B] etiqueta {14.5.2} ]
Arrhenius usó estas relaciones para llegar a una ecuación que relaciona la magnitud de la constante de velocidad para una reacción a la temperatura, la energía de activación y la constante, A , llamada factor de frecuencia :
[k = Ae ^ {- E _ { Large a} / RT} label {14.5.3} ]
El factor de frecuencia se utiliza para convertir las concentraciones en colisiones por segundo. Debido a que la frecuencia de las colisiones depende de la temperatura, A en realidad no es constante. En cambio, A aumenta ligeramente con la temperatura ya que el aumento de la energía cinética de las moléculas a temperaturas más altas hace que se muevan un poco más rápido y, por lo tanto, sufren más colisiones por unidad de tiempo. La ecuación ( ref {14.5.3} ) se conoce como ecuación de Arrhenius y resume el modelo de colisión de la cinética química, donde T es el absoluto temperatura (en K) y R es la constante de gas ideal [8.314 J / (K · mol)]. (E_a ) indica la sensibilidad de la reacción a los cambios de temperatura. La velocidad de reacción con un E a grande aumenta rápidamente con el aumento de la temperatura, mientras que la velocidad de reacción con un (E_a ) más pequeño aumenta mucho más lentamente con el aumento de la temperatura.
Si conocemos la velocidad de reacción a varias temperaturas, podemos usar la ecuación de Arrhenius para calcular la energía de activación. Tomando el logaritmo natural de ambos lados de Ecuación ( ref {14.5.3} ) ,
[ ln k = ln A + left (- dfrac {E _ { textrm a}} {RT} right) = ln A + left [ left (- dfrac {E _ { textrm a}} {R} right) left ( dfrac {1} {T} right) right] label {14.5.4} ]
La ecuación ( ref {14.5.4} ) es la ecuación de una línea recta, y = mx + b , donde y = ln k y x = 1 / T . Esto significa que una gráfica de ln k versus 1 / T es una línea recta con una pendiente de – E a / [19459016 ] R y una intersección de ln A . De hecho, necesitamos medir la velocidad de reacción a solo dos temperaturas para estimar E a .
Conocer el (E_a ) a una temperatura nos permite predecir la velocidad de reacción a otras temperaturas. Esto es importante en la cocina y la conservación de alimentos, por ejemplo, así como en el control de reacciones industriales para prevenir posibles desastres. El procedimiento para determinar (E_a ) a partir de las velocidades de reacción medidas a varias temperaturas se ilustra en el Ejemplo ( PageIndex {1} ).
Resumen
Para que ocurra una reacción química, se debe superar un umbral de energía, y las especies que reaccionan también deben tener la orientación espacial correcta. La ecuación de Arrhenius es (k = Ae ^ {- E _ { Large a} / RT} ). Se requiere una energía mínima (energía de activación, E a ) para que una colisión entre moléculas produzca una reacción química. Los gráficos de energía potencial para un sistema versus la coordenada de reacción muestran una barrera de energía que debe superarse para que ocurra la reacción. La disposición de los átomos en el punto más alto de esta barrera es el complejo activado, o estado de transición, de la reacción. A una temperatura dada, cuanto mayor sea E a , más lenta será la reacción. La fracción de orientaciones que dan como resultado una reacción es el factor estérico. El factor de frecuencia, el factor estérico y la energía de activación están relacionados con la constante de velocidad en la ecuación de Arrhenius: (k = Ae ^ {- E _ { Large a} / RT} ). Una gráfica del logaritmo natural de k versus 1 / T es una línea recta con una pendiente de – E a / [19459016 ] R .