Estos son ejercicios de tarea para acompañar el Mapa de texto creado para “Química: La ciencia central” por Brown et al. Se pueden encontrar bancos de preguntas de química general complementaria para otros mapas de texto y se puede acceder aquí . Además de estas preguntas disponibles públicamente, el acceso al banco privado de problemas para su uso en exámenes y tareas está disponible para los profesores solo de manera individual; comuníquese con Delmar Larsen para obtener una cuenta con permiso de acceso.
14.1: Factores que afectan las tasas de reacción
Q14.1.1
¿Qué información puedes obtener al estudiar la cinética química de una reacción? ¿Una ecuación química equilibrada proporciona la misma información? ¿Por qué o por qué no?
S14.1.1
Cinética proporciona información sobre la velocidad de reacción y el mecanismo de reacción; La ecuación química equilibrada da sólo la estequiometría de la reacción.
Q14.1.2
Si tuvieras la tarea de determinar si proceder con una reacción particular en una instalación industrial, ¿por qué sería importante para ti estudiar la cinética química de la reacción?
S14.1.2
El estudio de la cinética química determina si se debe proceder con una reacción, ya que mide la velocidad de una reacción. Las reacciones realizadas en una instalación industrial mezclan compuestos, calentándolos y agitándolos durante un tiempo, antes de pasar al siguiente proceso. Cuando los compuestos se trasladan a la siguiente fase del proceso, es importante saber cuánto tiempo durará la reacción en una etapa antes de continuar, para asegurarse de que la reacción haya finalizado antes de comenzar la siguiente
Q14.1.3
¿Cuál es la relación entre cada uno de los siguientes factores y la velocidad de reacción: concentración de reactivo, temperatura de la reacción, propiedades físicas de los reactivos, propiedades físicas y químicas del disolvente y la presencia de un catalizador?
S14.1.3
Concentración de reactivo:
La velocidad de reacción y la concentración de reactivos tienen una relación directa; A medida que aumenta la concentración, también lo hace la velocidad de reacción. Esto se debe a que una concentración más alta hace que los reactivos tengan una mayor probabilidad de colisionar con otra partícula reactiva, posiblemente induciendo la reacción química. Esto proviene de la teoría de la colisión.
Temperatura de reacción:
La velocidad de reacción y la temperatura de reacción también tienen una relación directa; A medida que aumenta la temperatura, también lo hace la velocidad de reacción. Una temperatura más alta hace que las partículas se muevan a una velocidad más rápida, por lo que cuando dos o más partículas reactivas colisionan, chocan con más energía y es más probable que alcancen el umbral de energía de activación, comenzando una reacción química.
Propiedades físicas de los reactivos:
Si los reactivos tienen las mismas propiedades físicas, es más probable que reaccionen, aumentando la velocidad de reacción, porque los reactivos se mezclan y tienen más probabilidades de colisionar con otro de los reactivos.
Propiedades físicas y químicas del disolvente:
Las propiedades del disolvente también afectan las velocidades de reacción. Alta viscosidad significa que las partículas son más lentas que en solventes de baja viscosidad, por lo que las velocidades de reacción son más lentas en solventes de alta viscosidad que en solventes de baja viscosidad. Esto indica una relación inversa entre la viscosidad y la velocidad de reacción.
Presencia de un catalizador:
La definición química de un catalizador en una sustancia que aumenta la velocidad de una reacción sin ser utilizada en la reacción. Por lo tanto, si hay un catalizador presente, la velocidad de reacción aumenta.
Q14.1.4
Una suspensión es una mezcla de un sólido finamente dividido con un líquido en el que solo es escasamente soluble. A medida que prepara una reacción, observa que uno de sus reactivos forma una suspensión con el disolvente, en lugar de una solución. ¿Qué efecto tendrá esto en la velocidad de reacción? ¿Qué pasos puedes tomar para tratar de resolver el problema?
Q14.1.5
¿Por qué aumenta la velocidad de reacción de prácticamente todas las reacciones con un aumento de la temperatura? Si hicieras un vaso de té helado endulzado a la antigua, agregando azúcar y cubitos de hielo a un vaso de té caliente, ¿cuál agregarías primero?
S14.1.5
El aumento de la temperatura aumenta la energía cinética promedio de las moléculas y los iones, lo que hace que choquen con mayor frecuencia y con mayor energía, lo que aumenta la velocidad de reacción. Primero disuelva el azúcar en el té caliente y luego agregue el hielo.
Q14.1.6
En un entorno de laboratorio típico, se lleva a cabo una reacción en una campana ventilada con circulación de aire proporcionada por el aire exterior. Un estudiante notó que una reacción que dio un alto rendimiento de un producto en el invierno dio un bajo rendimiento del mismo producto en el verano, a pesar de que su técnica no cambió y los reactivos y concentraciones utilizados fueron idénticos. ¿Cuál es una explicación plausible para los diferentes rendimientos?
Q14.1.7
Un área muy activa de investigación química implica el desarrollo de catalizadores solubilizados que no se vuelven inactivos durante el proceso de reacción. Se espera que tales catalizadores aumenten las velocidades de reacción significativamente en relación con la misma reacción realizada en presencia de un catalizador heterogéneo. ¿Cuál es la razón para anticipar que la tasa relativa aumentará?
Q14.1.8
El agua tiene una constante dieléctrica más de dos veces mayor que la del metanol (80.1 para H 2 O y 33.0 para CH 3 OH). ¿Cuál sería su solvente de elección para una reacción de sustitución entre un compuesto iónico y un reactivo polar, los cuales son solubles en metanol o agua? ¿Por qué?
14.2: Tasas de reacción
Q14.2.1
Explica por qué la velocidad de reacción es generalmente más rápida a intervalos de tiempo tempranos. Para el segundo orden A + B → C, ¿cómo sería la gráfica de la concentración de C versus tiempo durante el curso de la reacción?
S14.2.1
Las concentraciones de reactivo son más altas al comienzo de una reacción. La gráfica de [C] versus t es una curva con una pendiente que se vuelve cada vez menos positiva.
Q14.2.2
Explique las diferencias entre una ley de tasa diferencial y una ley de tasa integrada. ¿Qué dos componentes tienen en común? ¿Qué forma se prefiere para obtener un orden de reacción y una constante de velocidad? ¿Por qué?
Q14.2.3
Las reacciones controladas por difusión tienen velocidades que están determinadas solo por la velocidad de reacción a la que dos moléculas reactivas pueden difundirse juntas. Estas reacciones son rápidas, con constantes de velocidad de segundo orden típicamente del orden de 10 10 L / (mol · s). ¿Se espera que las reacciones sean más rápidas o más lentas en solventes que tienen una baja viscosidad? ¿Por qué? Considere las reacciones H 3 O + + OH – → 2H 2 O y H 3 O [19459389 ] + + N (CH 3 ) 3 → H 2 O + HN (CH 3 ) 3 + en solución acuosa. ¿Cuál tendría la constante de tasa más alta? ¿Por qué?
S14.2.3
Más rápido en un disolvente menos viscoso porque la velocidad de difusión es mayor; la reacción H 3 O + / OH – es más rápida debido a la disminución del tamaño relativo de los reactivos y la mayor atracción electrostática entre los reactivos.
Q14.2.4
¿Qué información se puede obtener del orden de reacción? ¿Qué correlación tiene el orden de reacción con la estequiometría de la ecuación general?
Q14.2.5
Durante la reacción de hidrólisis A + H 2 O → B + C, la concentración de A disminuye mucho más rápidamente en un disolvente polar que en un disolvente no polar. ¿Cómo se reflejaría este efecto en el orden general de reacción?
Q14.2.6
La velocidad de reacción de una reacción particular en la que A y B reaccionan para hacer C es la siguiente:
( textrm {rate} = – dfrac { Delta [ textrm A]} { Delta t} = dfrac {1} {2} left ( dfrac { Delta [ textrm C] } { Delta t} right) )
Escribe una ecuación de reacción que sea consistente con esta ley de velocidad. ¿Cuál es la expresión de velocidad con respecto al tiempo si 2A se convierten en 3C?
Q14.2.7
Mientras viajaba al trabajo, una persona condujo durante 12 minutos a 35 mph, luego se detuvo en una intersección durante 2 minutos, continuó el viaje a 50 mph durante 28 minutos, condujo lentamente a través del tráfico a 38 mph durante 18 minutos, y luego pasé 1 minuto en un estacionamiento a 3 mph. ¿Cuál fue la tasa promedio del viaje? ¿Cuál fue la frecuencia instantánea a los 13 min? a los 28 min?
Q14.2.8
¿Por qué la mayoría de los estudios de reacciones químicas utilizan las velocidades de reacción iniciales para generar una ley de velocidad? ¿Cómo se determina esta tasa inicial? Dados los siguientes datos, ¿cuál es el orden de reacción? Estimar.
| Hora (s) | [A] (M) |
|---|---|
| 120 | 0,158 |
| 240 | 0,089 |
| 360 | 0,062 |
Q14.2.9
Predice cómo se verá afectada la velocidad de reacción al duplicar la concentración de la primera especie en cada ecuación.
- C 2 H 5 I → C 2 H 4 + HI: tasa = k [ C 2 H 5 I]
- SO + O 2 → SO 2 + O: tasa = k [SO] [O 2 ]
- 2CH 3 → C 2 H 6 : tasa = k [CH 3 ] [19459389 ] 2
- ClOO → Cl + O 2 : tasa = k
Q14.2.10
Escisión de C 2 H 6 para producir dos radicales CH 3 · es una reacción en fase gaseosa que ocurre a 700 ° C. Esta reacción es de primer orden, con k = 5,46 × 10 −4 s −1 . ¿Cuánto tardará la reacción en llegar al 15%? al 50% de finalización?
S14.2.10
298 s; 1270 s
Q14.2.11
Tres procesos químicos ocurren a una altitud de aproximadamente 100 km en la atmósfera de la Tierra.
[ mathrm {N_2 ^ +} + mathrm {O_2} xrightarrow {k_1} mathrm {N_2} + mathrm {O_2 ^ +} ]
[ mathrm {O_2 ^ +} + mathrm {O} xrightarrow {k_2} mathrm {O_2} + mathrm {O ^ +} ]
[( mathrm {O ^ +} + mathrm {N_2} xrightarrow {k_3} mathrm {NO ^ +} + mathrm {N} ]
Escribe una ley de velocidad para cada reacción elemental. Si se determina que la ley de velocidad para la reacción general es velocidad = k [N 2 + ] [O 2 ], que Uno de los pasos es la limitación de velocidad?
Q14.2.12
La oxidación del yoduro acuoso por el ácido arsénico para dar I 3 – y el ácido arsenioso se realiza a través de la siguiente reacción:
Escriba una expresión para la tasa inicial de disminución de [I 3 – ], Δ [I 3 – ] / Δt. Cuando la velocidad de reacción de la reacción directa es igual a la de la reacción inversa: k f / k r = [H 3 AsO 3 [ 19459376]] [I 3 – ] / [H 3 AsO 4 ] [I – ] [ 19459389] 3 [H + ] 2 . Con base en esta información, ¿qué puede decir sobre la naturaleza de los pasos determinantes de la velocidad para las reacciones inversa y directa?
14.3: Concentración y velocidad
14.4: El cambio de concentración con el tiempo
Q14.4.1
¿Cuáles son las características de una reacción de orden cero? Experimentalmente, ¿cómo determinaría si una reacción es de orden cero?
Q14.4.2
Predice si las siguientes reacciones son de orden cero y explica tu razonamiento.
- una reacción de sustitución de un alcohol con HCl para formar un haluro de alquilo y agua
- hidrogenación catalítica de un alqueno
- hidrólisis de un haluro de alquilo a un alcohol
- conversión enzimática de nitrato a nitrito en una bacteria del suelo
Q14.4.3
En una reacción de primer orden, ¿cuál es la ventaja de usar la ley de tasa integrada expresada en logaritmos naturales sobre la ley de tasa expresada en forma exponencial?
Q14.4.4
Si la velocidad de reacción es directamente proporcional a la concentración de un reactivo, ¿qué le dice esto sobre (a) el orden de reacción con respecto al reactivo y (b) el orden de reacción general?
Q14.4.5
La reacción de NO con O 2 se encuentra en segundo orden con respecto a NO y primer orden con respecto a O 2 . ¿Cuál es el orden general de reacción? ¿Cuál es el efecto de duplicar la concentración de cada reactivo en la velocidad de reacción?
Q14.4.6
El yoduro reduce el Fe (III) de acuerdo con la siguiente reacción:
[2Fe ^ {3 +} (solución) + 2I ^ – (solución) → 2Fe ^ {2 +} (solución) + I_2 (solución) ]
Experimentalmente, se encontró que duplicar la concentración de Fe (III) duplicó la velocidad de reacción, y duplicar la concentración de yoduro aumentó la velocidad de reacción en un factor de 4. ¿Cuál es el orden de reacción con respecto a cada especie? ¿Cuál es la ley general de tarifas? ¿Cuál es el orden general de reacción?
S14.4.6
Primer orden en Fe 3 + ; segundo orden en I – ; tercer orden en general; tasa = k [Fe 3 + ] [I – ] 2 .
Q14.4.7
El peróxido de benzoilo es un medicamento utilizado para tratar el acné. Su velocidad de descomposición térmica a varias concentraciones se determinó experimentalmente, y los datos se tabularon de la siguiente manera:
| Experimento | [Peróxido de benzoilo] 0 (M) | Tasa inicial (M / s) |
|---|---|---|
| 1 | 1,00 | 2,22 × 10 −4 |
| 2 | 0,70 | 1,64 × 10 −4 |
| 3 | 0,50 | 1,12 × 10 −4 |
| 4 | 0,25 | 0,59 × 10 −4 |
¿Cuál es el orden de reacción con respecto al peróxido de benzoilo? ¿Cuál es la ley de tasas para esta reacción?
S14.4.7
La ley de velocidad general es: velocidad = k [peróxido de benzoilo] m . Para encontrar el orden de reacción con respecto al peróxido de benzoilo, divida dos leyes de velocidad y resuelva para m:
( dfrac {rate_2} {rate_1} = dfrac {k_2} {k_1} left ( dfrac {[Benzoyl Peroxide] _2} {[Benzoyl Peroxide] _1} right) ^ m ) [19459338 ]
( dfrac {1.64 × 10 ^ -4 dfrac {M} {s}} {2.22 × 10 ^ -4 dfrac {M} {s}} = ( dfrac {0.070 M} {1.00 M }) ^ m )
(0.738 = (0.7) ^ m )
(m = 0,85 )
ley de velocidad: velocidad = k [peróxido de benzoilo] 0.85
Q14.4.8
El 1-bromopropano es un líquido incoloro que reacciona con S 2 O 3 2− según la siguiente reacción:
[C_3H_7Br + S_2O_3 ^ {2−} → C_3H_7S_2O_3 ^ – + Br ^ – ]
La reacción es de primer orden en 1-bromopropano y de primer orden en S 2 O 3 2− , con una velocidad constante de 8.05 × 10 [ 19459389] −4 M −1 · s −1 . Si comenzó una reacción con 40 mmol / 100 mL de C 3 H 7 Br y una concentración equivalente de S 2 O 3 2− , ¿cuál sería la velocidad de reacción inicial? Si tuviera que disminuir la concentración de cada reactivo a 20 mmol / 100 ml, ¿cuál sería la velocidad de reacción inicial?
S14.4.8
1,29 × 10 −4 M / s; 3.22 × 10 −5 M / s
Q14.4.9
Se encontró que la ley de velocidad experimental para la reacción 3A + 2B → C + D era Δ [C] / Δ t = k [A] 2 [ 19459390] [B] para una reacción general que es de tercer orden. Debido a que el análisis gráfico es difícil más allá de las reacciones de segundo orden, explique el procedimiento para determinar la ley de velocidad experimentalmente.
14.5: Temperatura y velocidad
Q14.5.1
Aunque un aumento en la temperatura da como resultado un aumento en la energía cinética, este aumento en la energía cinética no es suficiente para explicar la relación entre la temperatura y las velocidades de reacción. ¿Cómo se relaciona la energía de activación con la cinética química de una reacción? ¿Por qué un aumento en la temperatura aumenta la velocidad de reacción a pesar del hecho de que la energía cinética promedio es aún menor que la energía de activación?
S14.5.1
Se requiere energía de activación para que una colisión entre moléculas produzca una reacción química, y también está relacionada con la velocidad debida a la ecuación de Arrhenius
La energía de activación es el umbral de energía necesaria para que se produzca una reacción. Las partículas reactivas deben colisionar con suficiente energía para poder romper enlaces químicos, lo que permitirá la creación de nuevos enlaces. Si las partículas no tienen suficiente energía, cuando chocan, simplemente rebotarán entre sí.
k = Ae (-Ea / RT) . El aumento de la temperatura aumenta la velocidad de reacción a pesar de que la cinética promedio es menor que la energía de activación, ya que aumenta la velocidad de colisión entre las moléculas.
Con un aumento de la temperatura, hay una mayor distribución de energía cinética entre las partículas reactivas. Este aumento de temperatura permite que aumente la velocidad en que las partículas chocan entre sí. Aunque la energía cinética promedio es aún más baja que la energía de activación, el aumento de colisiones entre partículas aumenta la posibilidad de que las partículas que contienen suficiente energía superen la barrera de energía para colisionar. Por lo tanto, la velocidad de reacción aumenta debido a esta mayor velocidad de colisiones.
Además, hay una mayor cantidad de moléculas que tienen suficiente energía cinética para superar la barrera energética, a pesar de que la energía promedio de todas estas moléculas sigue siendo inferior a la energía de activación.
Q14.5.2
Para cualquier reacción dada, ¿cuál es la relación entre la energía de activación y cada una de las siguientes?
- repulsiones electrostáticas
- formación de enlaces en el complejo activado
- la naturaleza del complejo activado
S14.5.2
1.) Repulsión electrostática: la repulsión electrostática es la interacción desfavorable entre dos especies de carga similar. La energía de activación es la cantidad mínima de energía necesaria para que ocurra una reacción. Las moléculas que reaccionan deben tener suficiente energía para vencer la repulsión electrostática, y se requiere una cantidad mínima de energía para romper los enlaces químicos para que se puedan formar nuevos.
2.) Formación de enlace en el complejo activado: Un complejo activado es un estado intermedio que se forma durante la conversión de reactivos en productos. La ruptura de enlaces puede aumentar la energía de activación ya que romper enlaces requiere energía.
3.) Naturaleza del complejo activado: la energía de activación de una reacción química es la diferencia entre la energía del complejo activado y la energía de los reactivos. Si la estructura tiene un alto impedimento estérico, la energía de activación será mayor.
Q14.5.3
Si le preocupa si una reacción ocurrirá rápidamente, ¿por qué estaría más interesado en conocer la magnitud de la energía de activación que el cambio en la energía potencial para la reacción?
Q14.5.4
El producto C en la reacción A + B → C + D se puede separar fácilmente de la mezcla de reacción. Le han dado A puro y B puro y le dicen que determine la energía de activación para esta reacción para determinar si la reacción es adecuada para la síntesis industrial de C. ¿Cómo haría esto? ¿Por qué necesita saber la magnitud de la energía de activación para tomar una decisión sobre la viabilidad?
Q14.5.5
Arriba E a , las moléculas colisionan con suficiente energía para superar la barrera energética para una reacción. ¿Es posible que ocurra una reacción a una temperatura inferior a la necesaria para alcanzar E a ? Explica tu respuesta.
Q14.5.6
¿Cuál es la relación entre A , E a y T ? ¿Cómo afecta un aumento de A a la velocidad de reacción?
Q14.5.7
De dos reacciones altamente exotérmicas con diferentes valores de E a , que necesitarían ser monitoreadas más cuidadosamente: ¿la que tiene el valor más pequeño o la que tiene el valor más alto? ¿Por qué?
Q14.5.8
¿Qué sucede con la velocidad aproximada de una reacción cuando la temperatura de la reacción aumenta de 20 ° C a 30 ° C? ¿Qué sucede con la velocidad de reacción cuando la temperatura se eleva a 70 ° C? Para una reacción dada a temperatura ambiente (20 ° C), ¿cuál es la forma de un gráfico de la velocidad de reacción frente a la temperatura a medida que la temperatura aumenta a 70 ° C?
S14.5.8
La velocidad de reacción se duplicará aproximadamente: 20 ° C a 30 ° C, la velocidad de reacción aumenta en aproximadamente 2 1 = 2; 20 ° C a 70 ° C, la velocidad de reacción aumenta en aproximadamente 2 5 = 32 veces. Una gráfica de la velocidad de reacción versus temperatura dará un aumento exponencial: velocidad ∝ 2 Δ T / 10
Q14.5.9
El acetaldehído, utilizado en espejos plateados y algunos perfumes, sufre una descomposición de segundo orden entre 700 y 840 K. Según los datos de la siguiente tabla, ¿diría usted que el acetaldehído sigue la regla general de que cada aumento de 10 K en la temperatura se duplica? la velocidad de reacción?
| T (K) | k (M −1 · s −1 ) |
| 720 | 0,024 |
| 740 | 0,051 |
| 760 | 0,105 |
| 800 | 0,519 |
Q14.5.10
El bromoetano reacciona con el ion hidróxido en agua para producir etanol. La energía de activación para esta reacción es 90 kJ / mol. Si la velocidad de reacción es 3.6 × 10 −5 M / sa 25 ° C, ¿cuál sería la velocidad de reacción a las siguientes temperaturas?
- 15 ° C
- 30 ° C
- 45 ° C
Q14.5.11
Una reacción catalizada por enzimas tiene una energía de activación de 15 kcal / mol. ¿Cómo diferiría el valor de la constante de velocidad entre 20 ° C y 30 ° C? Si la enzima redujo la (E_a ) de 25 kcal / mol a 15 kcal / mol, ¿por qué factor la enzima aumentó la velocidad de reacción a cada temperatura?
S14.5.11
- 1,0 × 10 −5 M / s
- 6,6 × 10 −5 M / s
- 3,5 × 10 −4 M / s
Q14.5.12
Los datos en la siguiente tabla son las constantes de velocidad en función de la temperatura para la dimerización de 1,3-butadieno. ¿Cuál es la energía de activación para esta reacción?
| T (K) | k (M −1 · min −1 ) |
| 529 | 1,4 |
| 560 | 3,7 |
| 600 | 25 |
| 645 | 82 |
S14.5.12
100 kJ / mol
Q14.5.13
La velocidad de reacción a 25 ° C es 1.0 × 10 −4 M / s. El aumento de la temperatura a 75 ° C hace que la velocidad de reacción aumente a 7.0 × 10 −2 M / s. Estime (E_a ) para este proceso. Si (E_a ) fuera 25 kJ / mol y la velocidad de reacción a 25 ° C es 1.0 × 10 −4 M / s, ¿cuál sería la velocidad de reacción a 75 ° C?
14.6: Mecanismos de reacción
Q14.6.1
¿Cómo se relaciona el término molecularidad con las reacciones elementales? ¿Cómo se relaciona con la ecuación química equilibrada general?
Q14.6.2
¿Cuál es la relación entre el orden de reacción y la molecularidad de una reacción? ¿Cuál es la relación entre el orden de reacción y la ecuación química equilibrada?
Q14.6.3
Cuando determina la ley de velocidad para una reacción dada, ¿por qué es válido suponer que la concentración de un intermedio no cambia con el tiempo durante el curso de la reacción?
Q14.6.3
Si conoces la ley de velocidad para una reacción general, ¿cómo determinarías qué reacción elemental determina la velocidad? Si un paso intermedio determina la velocidad, ¿cómo puede derivarse de este paso la ley de velocidad determinada experimentalmente para la reacción?
Q14.6.4
Give the rate-determining step for each case.
- Traffic is backed up on a highway because two lanes merge into one.
- Gas flows from a pressurized cylinder fitted with a gas regulator and then is bubbled through a solution.
- A document containing text and graphics is downloaded from the Internet.
Q14.6.5
Before being sent on an assignment, an aging James Bond was sent off to a health farm where part of the program’s focus was to purge his body of radicals. Why was this goal considered important to his health?
S14.6.5
Free radicals are uncharged molecules with an unpaired valence electron. The reason these are so dangerous is because they like to grab electrons from other atoms to fill their own outer shell. This allows them to impair protein function because free radicals readily oxidize proteins and cell membrane which could lead to a loss of function. It was important to purge James Bond of radicals because radicals set off chain reactions of continuously pulling electrons from molecules, which in turn, can damage cells in the body.
Q14.6.6
Cyclopropane, a mild anesthetic, rearranges to propylene via a collision that produces and destroys an energized species. The important steps in this rearrangement are as follows:
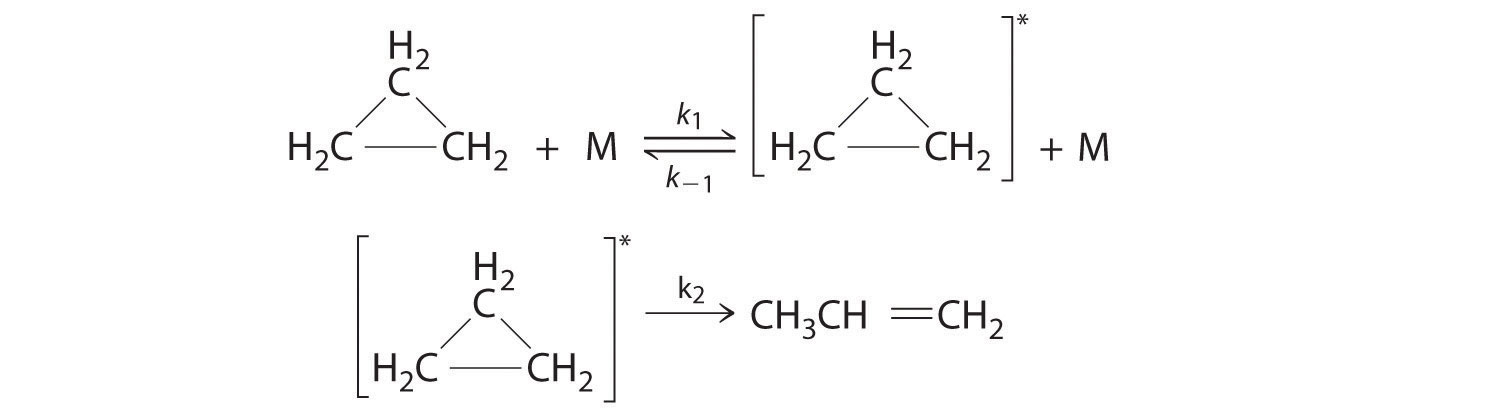
where M is any molecule, including cyclopropane . Only those cyclopropane molecules with sufficient energy (denoted with an asterisk) can rearrange to propylene. Which step determines the rate constant of the overall reaction?
S14.6.6
When we are trying to decide which step is a rate-determining step, you have to look at which step is the slowest of them all, since we have no knowledge of the time scale for either of these steps we have to look elsewhere to determine the rate-determining step.
In our specific problem, we do not know what exact molecules we have however we do see that the first step is an equilibrium since it has a double-headed arrow with two k values one that is the reciprocal of the other. Since it is an equilibrium we can reasonably assume that energized propane is rapidly created which would lead us to the conclusion that the second step is the slower of the two steps and is, therefore, the rate-determining step. So, the second step (with k 2 ) determines the rate constant of the overall reaction.
Q14.6.7
Above approximately 500 K, the reaction between NO 2 and CO to produce CO 2 and NO follows the second-order rate law Δ[CO 2 ]/Δ t = k [NO 2 ][CO]. At lower temperatures, however, the rate law is Δ[CO 2 ]/Δ t = k ′[NO 2 ] 2 , for which it is known that NO 3 is an intermediate in the mechanism. Propose a complete low-temperature mechanism for the reaction based on this rate law. Which step is the slowest?
S14.6.7
Given that NO 3 is an intermediate in the low temperature reaction mechanism, we automatically know two things: 1) NO 3 won’t show up in the final overall reaction , and thus, 2) NO 3 will be in the products of the first reaction of the mechanism and in the reactants of the second reaction . We can also assume that since we’re given an intermediate from the problem, this is the only intermediate (so we won’t have to dream up any other compounds that might exist in the series of reactions.) These things being said, the lower temperature reaction mechanism will look like this:
[2NO_2(g) rightarrow NO_3(g) + NO(g) tag{1}]
[CO(g) + NO_3(g) rightarrow CO_2(g) + NO_2(g) tag{2}]
And the overall reaction will look like this (notice how NO 3 is not present):
[CO(g) + NO_2(g) rightarrow CO_2(g) + NO(g) tag{overall reaction}]
Now that we have the reaction mechanism written out, we can go about determining which step is the slowest. It would be pretty tricky to do this if we weren’t given any further information, however, we know two more things: 1) the high-temperature mechanism’s rate = k[NO 2 ][CO] meaning that it took place in one step (given that the overall reaction is also equal to this rate) and 2) the low-temperature mechanism’s rate = k′[NO 2 ] 2 . These two things being said, we’ve both confirmed that our proposed low-temperature reaction mechanism is in fact two steps, and that we have a means to find which step is slower .
By using the “guess-and-check” method we can label each step reaction one at a time as the “slow reaction” and see if the rate matches up with the rate given to us.
Let’s first try the 2nd reaction. (see above)
By using rate laws we can determine that the rate of the reaction must be in terms of its reactants, which follows:
[textrm{k}textrm{[CO][NO}_3textrm{]}]
… But wait! We can’t have the overall reaction rate in terms of an intermediate.
By looking at the 1st reaction, we can determine that we can sub in “[NO 2 ] /[NO]” for “[NO 3 ]” since by writing the full reaction rate of the first step and solving for [NO 3 ] this is equivalent. So, we now have the overall rate of the mechanism as the following given the 2nd reaction is the “slow reaction:”
[textrm{k}dfrac{textrm{[CO][NO}_2textrm{]}^2}{textrm{[NO}textrm{]}}]
Note that NO 2 is raised to the second power to account for the stoichiometry of the balanced reaction.
So clearly the 2nd reaction isn’t the slow reaction since the rate is not equivalent to what we were given!
Let’s check the rate of the 1st reaction now…
[textrm{k}textrm{[NO}_2textrm{]}^2]
What do you know… the rates are equal!
We have now confirmed that the 1st reaction is the slow reaction equation, since its rate is equivalent to the overall reaction rate.
Q14.6.8
Nitramide (O 2 NNH 2 ) decomposes in aqueous solution to N 2 O and H 2 O. What is the experimental rate law (Δ[N 2 O]/Δ t ) for the decomposition of nitramide if the mechanism for the decomposition is as follows?
| (mathrm{O_2NNH_2}overset{k_1}{underset{k_{-1}}{rightleftharpoons}}mathrm{O_2NNH^-}+mathrm{H^+}) | ((textrm{fast})) |
| (mathrm{O_2NNH^-}xrightarrow{k_2}mathrm{N_2O}+mathrm{OH^-}) | ((textrm{slow})) |
| (mathrm{H^+}+mathrm{OH^-}xrightarrow{k_3}mathrm{H_2O}) | ((textrm{fast})) |
Assume that the rates of the forward and reverse reactions in the first equation are equal.
S14.6.8
We know that the slowest step of the reaction is the rate determining step, since it usually has the highest activation energy requirement. As a result, the slowest step of the reaction is the experimental rate law we are looking for.
Note: since the slowest step is the rate determining step, that usually means there is some intermediate in between. Intermediates should NEVER be a part of the rate law mechanism.
$$rate = rate_2 = {k_2}{[O_2NNH^{-}]}$$
Since Nitramide is an intermediate, we must find some way to substitute it. To solve that problem, we look for where Nitramide is produced and consumed. We see that
$$rate_1 = {k_1}{[O_2NNH_2]}$$
$$rate_{-1} = {k_{-1}}{[O_2NNH^-]}{[H^+]}$$
Since these two rates produce and consume the same amount of (O_2NNH^{-}) over the same time period, we can set them equal to each other and solve for the intermediate
$$rate_1 = rate_{-1}$$
$${k_1}{[O_2NNH_2]} = {k_{-1}}{[O_2NNH^-]}{[H^+]}$$
$${[O_2NNH^-]} = frac{k_1{[O_2NNH_2]}}{k_{-1}{[H^+]}}$$
Substituting this equation back into our original equation gives us
$$rate=rate_2=k_2frac{k_1[O_2NNH_2]}{k_{-1}[H^+]}$$
With all of the rate constants (k), we can clean up our equation a little bit by saying
$$k = frac{k_2{k_1}}{k_{-1}}$$
Leaving us with
$$rate = frac{k[O_2NNH_2]}{[H^+]}$$
A14.6.8
(textrm{rate}=k_2dfrac{k_1[mathrm{O_2NNH_2}]}{k_{-1}[mathrm{H^+}]}=kdfrac{[mathrm{O_2NNH_2}]}{[mathrm{H^+}]})
Q14.6.9
The following reactions are given:
[mathrm{A+B}overset{k_1}{underset{k_{-1}}{rightleftharpoons}}mathrm{C+D}]
[mathrm{D+E}xrightarrow{k_2}mathrm F]
What is the relationship between the relative magnitudes of (k_{−1}) and (k_2) if these reactions have the following rate law?
[dfrac{Δ[F]}{Δt} = kdfrac{[A][B][E]}{[C]}]
How does the magnitude of (k_1) compare to that of (k_2)? Under what conditions would you expect the rate law to be
[dfrac{Δ[F]}{Δt} =k′[A][B]?]
Assume that the rates of the forward and reverse reactions in the first equation are equal.
S14.6.9
First, because we have broken the equations down into elementary steps we can write the rate laws for each step.
Step1:
[A+Bxrightarrow[]{k_{1}} C+D]
[rate=k_{1}[A][B]]
Step 2:
[C+D xrightarrow[]{k_{-1}} A+B]
[rate=k_{-1}[C][D]]
Step 3:
[D+E xrightarrow[]{k_{2}} F]
[rate=k_{2}[D][E]]
If we add a these steps together we see that we get overall reaction
[A+B+E rightarrow C+F]
we can see that [D] is an intermediate and [k_{1}=k_{-1}] .
Since we are not told which steps are fast or slow we need to use Steady State Approximation.
If the second step is the slower step ( k- 1 >> k 2 ) then our rate determining step would be
[rate=k_{2}[D][E]]
Since we can only write rate laws in terms of products and reactants we have to rewrite this so that we are not including an intermediate .
Assume: rate of [D] formation = rate of its disappearance
[k_{1}[A][B]=k_{-1}[C][D]+k_{2}[D][E]]
[k_{1}[A][B]=[D](k_{-1}[C]+k_{2}[E])]
Solving for [D] we find that
[[D]= frac{k_{1}[A][B]}{(k_{-1}[C]+k_{2}[E])}]
now we can use this to substitute the intermediate [D] in the rate law to get an appropriate rate law.
[rate=frac{k_{2} k_{1}[A][B][E]}{(k_{-1}[C]+k_{2}[E])}]
because we had already established k- 1 >> k 2 we can assume that
[k_{-1}[C]+k_{2}[E]approx k_{-1}[C]]
this would give us the observed rate law
[frac{Delta [F]}{Delta t}=frac{k_{2}k_{1}[A][B][E]}{k_{-1}[C]}]
to make this clearer we can set
[k=frac{(k_{2})(k_{1})}{(k_{-1})}]
and we can then simplify it down to
[dfrac{Δ[F]}{Δt} = kdfrac{[A][B][E]}{[C]}]
we can see that all of these rate constants are related by this ratio k 2 k 1 / k- 1. Since k 2 is our rate determining step k- 1 >> k 2 and since k 1 = k- 1 then we can see that k 1 >> k 2.
We would expect the rate law to be
[dfrac{Δ[F]}{Δt} =k′[A][B]?]
if the rate determining step aka the slowest step is that corresponding to (step 1) since the rate law for this step is k 1 [A][B] and this is the exact the same as the rate law that we were given.
14.7: Catalysis
Q14.7.1
What effect does a catalyst have on the activation energy of a reaction? What effect does it have on the frequency factor ( A )? What effect does it have on the change in potential energy for the reaction?
S14.7.1
A catalyst lowers the activation energy of a reaction. Some catalysts can also orient the reactants and thereby increase the frequency factor. Catalysts have no effect on the change in potential energy for a reaction.
Q14.7.2
How is it possible to affect the product distribution of a reaction by using a catalyst?
Q14.7.3
A heterogeneous catalyst works by interacting with a reactant in a process called adsorption . What occurs during this process? Explain how this can lower the activation energy.
S14.7.3
In adsorption, a reactant binds tightly to a surface. Because intermolecular interactions between the surface and the reactant weaken or break bonds in the reactant, its reactivity is increased, and the activation energy for a reaction is often decreased.
Q14.7.4
What effect does increasing the surface area of a heterogeneous catalyst have on a reaction? Does increasing the surface area affect the activation energy? Explica tu respuesta.
Q14.7.5
Identify the differences between a heterogeneous catalyst and a homogeneous catalyst in terms of the following.
- ease of recovery
- collision frequency
- temperature sensitivity
- cost
S14.7.4
- Heterogeneous catalysts are easier to recover.
- Collision frequency is greater for homogeneous catalysts.
- Homogeneous catalysts are often more sensitive to temperature.
- Homogeneous catalysts are often more expensive.
Q14.7.6
An area of intensive chemical research involves the development of homogeneous catalysts, even though homogeneous catalysts generally have a number of operational difficulties. Propose one or two reasons why a homogenous catalyst may be preferred.
S14.7.6
Catalysts are compounds that, when added to chemical reactions, reduce the activation energy and increase the reaction rate. The amount of a catalyst does not change during a reaction, as it is not consumed as part of the reaction process. Catalysts lower the energy required to reach the transition state of the reaction, allowing more molecular interactions to achieve that state. However, catalysts do not affect the degree to which a reaction progresses. In other words, though catalysts affect reaction kinetics, the equilibrium state remains unaffected.
Catalysts can be classified into two types: homogenous and heterogeneous. Homogenous catalysts are those which exist in the same phase (gas or liquid) as the reactants, while heterogeneous catalysts are not in the same phase as the reactants. Typically, heterogeneous catalysis involves the use of solid catalysts placed in a liquid reaction mixture. For this question, we will be discussing homogenous catalysts.
Most of the times, homogeneous catalysis involves the introduction of an aqueous phase catalyst into an aqueous solution of reactants. One reason why homogeneous catalysts are preferred over heterogeneous catalysts because homogeneous catalysts mix well in chemical reactions in comparison to heterogeneous catalysts. However, homogeneous catalyst is often irrecoverable after the reaction has run to completion.
Q14.7.7
Consider the following reaction between cerium(IV) and thallium(I) ions:
[ce{2Ce^{4+} + Tl^+ → 2Ce^{3+} + Tl^{3+}}]
This reaction is slow, but Mn 2+ catalyzes it, as shown in the following mechanism:
[ce{Ce^{4+} + Mn^{2+} → Ce^{3+} + Mn^{3+}}]
[ce{Ce^{4+} + Mn^{3+} → Ce^{3+} + Mn^{4+}}]
[ce{Mn^{4+} + Tl^{+ }→ Tl^{3+} + Mn^{2+}}]
In what way does (Mn^{2+}) increase the reaction rate?
S14.7.7
The Mn 2+ ion donates two electrons to Ce 4+ , one at a time, and then accepts two electrons from Tl + . Because Mn can exist in three oxidation states separated by one electron, it is able to couple one-electron and two-electron transfer reactions.
Q14.7.8
The text identifies several factors that limit the industrial applications of enzymes. Still, there is keen interest in understanding how enzymes work for designing catalysts for industrial applications. ¿Por qué?
S14.7.8
Enzymes are expensive to make, denature and fail at certain temperatures, are not that stable in a solution, and are very specific to the reaction it was made for. However, scientists can use the observations from enzymes to create catalysts that are more effective in aiding the reaction and cost less to produce. Overall, catalysts still play a large part in lowering the activation energy for reactions. Creating new catalysts can help in the improvement of areas such as medical, ecological, and even commercial products.
Q14.7.9
Most enzymes have an optimal pH range; however, care must be taken when determining pH effects on enzyme activity. A decrease in activity could be due to the effects of changes in pH on groups at the catalytic center or to the effects on groups located elsewhere in the enzyme. Both examples are observed in chymotrypsin, a digestive enzyme that is a protease that hydrolyzes polypeptide chains. Explain how a change in pH could affect the catalytic activity due to (a) effects at the catalytic center and (b) effects elsewhere in the enzyme. ( Hint : remember that enzymes are composed of functional amino acids.)
Q14.7.10
At some point during an enzymatic reaction, the concentration of the activated complex, called an enzyme–substrate complex ((ES)), and other intermediates involved in the reaction is nearly constant. When a single substrate is involved, the reaction can be represented by the following sequence of equations:
[text {enzyme (E) + substrate (S)} rightleftharpoons text{enzyme-substrate complex (ES)} rightleftharpoons text{enzyme (E) + product (P)}]
This can also be shown as follows:
[E + S underset{k_{-1}}{stackrel{k_1}{rightleftharpoons}} ES underset{k_{-2}}{stackrel{k_{2}}{rightleftharpoons}} E+P]
Using molar concentrations and rate constants, write an expression for the rate of disappearance of the enzyme–substrate complex. Typically, enzyme concentrations are small, and substrate concentrations are high. If you were determining the rate law by varying the substrate concentrations under these conditions, what would be your apparent reaction order?
S14.7.10
Q14.7.11
A particular reaction was found to proceed via the following mechanism:
- (A + B → C + D) (slow)
- (2C → E) (fast)
- (E + A → B + F) (fast)
What is the overall reaction? Is this reaction catalytic, and if so, what species is the catalyst? Identify the intermediates
Q14.7.12
A particular reaction has two accessible pathways (A and B), each of which favors conversion of X to a different product ( Y and Z , respectively). Under uncatalyzed conditions pathway A is favored, but in the presence of a catalyst pathway B is favored. Pathway B is reversible, whereas pathway A is not. Which product is favored in the presence of a catalyst? without a catalyst? Draw a diagram illustrating what is occurring with and without the catalyst.
S14.7.12
In both cases, the product of pathway A is favored. All of the Z produced in the catalyzed reversible pathway B will eventually be converted to X as X is converted irreversibly to Y by pathway A.
Q14.7.13
The kinetics of an enzyme-catalyzed reaction can be analyzed by plotting the reaction rate versus the substrate concentration. This type of analysis is referred to as a Michaelis–Menten treatment. At low substrate concentrations, the plot shows behavior characteristic of first-order kinetics, but at very high substrate concentrations, the behavior shows zeroth-order kinetics. Explain this phenomenon.