Una placa metálica de plano infinito está en el plano (xy ). Se coloca una carga puntual + (Q ) en el eje (z ) – a una altura (h ) sobre la placa. En consecuencia, los electrones serán atraídos a la parte de la placa inmediatamente debajo de la carga, de modo que la placa llevará una densidad de carga negativa (σ ) que es mayor en el origen y que cae con la distancia ( rho ) desde el origen. ¿Podemos determinar (σ ( rho) )? Ver Figura (II.2 )
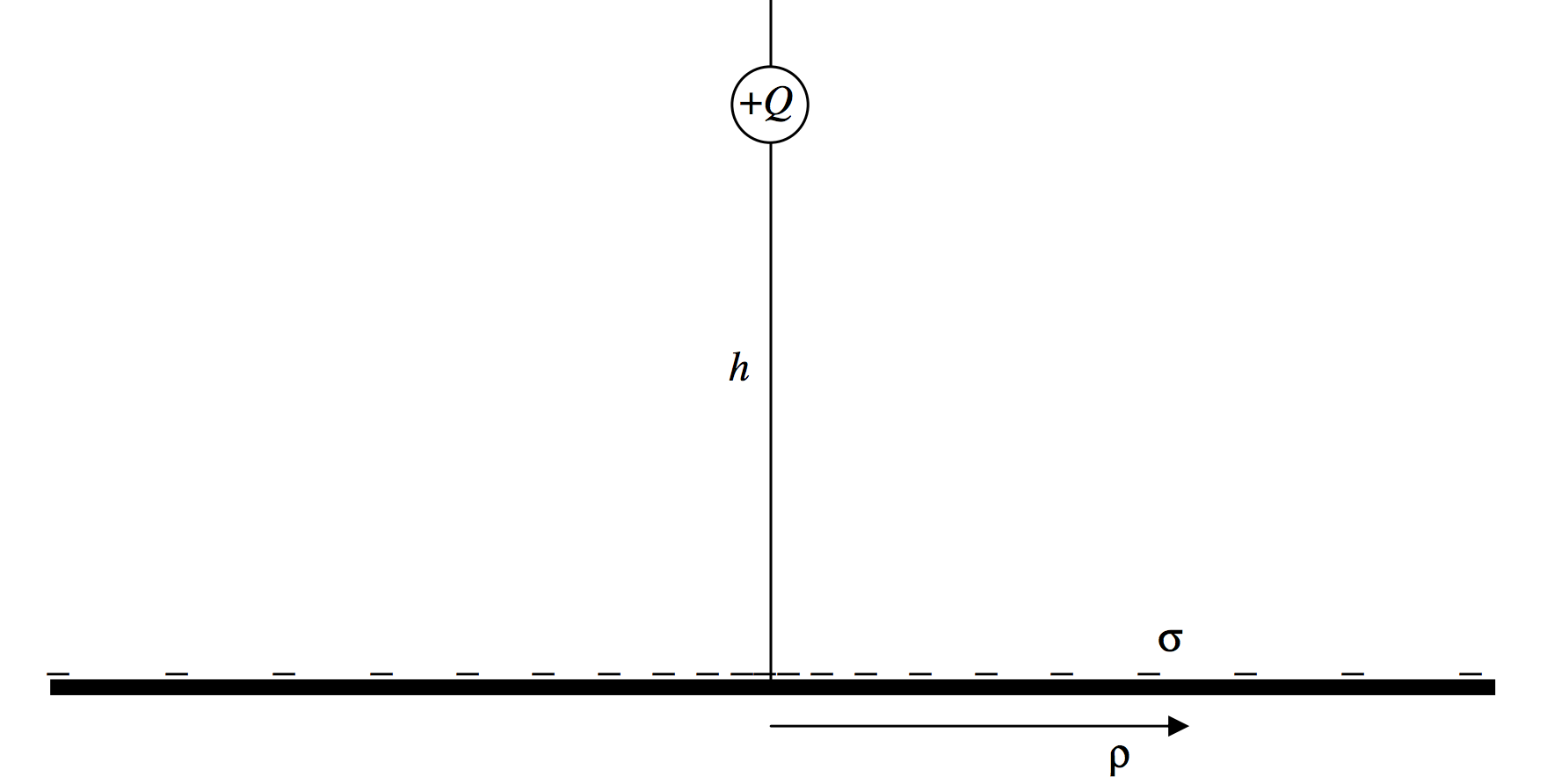
( text {FIGURE II.2} )
Primero, tenga en cuenta que el La superficie metálica, como conductor, es una superficie equipotencial , como lo es cualquier superficie metálica. El potencial es uniforme en cualquier lugar de la superficie. Ahora suponga que, en lugar de la superficie metálica, tenemos (además de la carga + (Q ) a una altura (h ) por encima del plano (xy ) -), una segunda carga puntual, – (Q ), a una distancia (h ) debajo del plano (xy ). El potencial en el plano (xy ) sería, por simetría, uniforme en todas partes. Es decir que el potencial en el plano (xy ) – es el mismo que en el caso de la carga de un solo punto y la placa de metal, y de hecho el potencial en cualquier punto sobre el plano es el mismo en ambos casos. Con el fin de calcular el potencial, podemos reemplazar la placa de metal por una imagen de la carga puntual. Es fácil calcular el potencial en un punto ((z, rho) ). Si suponemos que la permitividad por encima de la placa es ( epsilon_0 ), el potencial en ((z, rho) ) es
[ label {2.4.1} V = frac {Q} {4 pi epsilon_0} left ( frac {1} {[ rho ^ 2 + (hz) ^ 2] ^ {1/2}} – frac {1} {[ rho ^ 2 + (h + z) ^ 2] ^ {1/2}} right) ]
La intensidad de campo (E ) en el plano (xy ) – es – (∂V / ∂z ) evaluado en (z = 0 ), y esto es
[ label {2.4.2} E = – frac {2Q} {4 pi epsilon_0} cdot frac {h} {( rho ^ 2 + h ^ 2) ^ {3/2}}. ]
El campo (D ) – es ( epsilon_0 ) veces esto, y dado que todas las líneas de fuerza están por encima de la placa metálica, el teorema de Gauss establece que la densidad de carga es (σ = D ), y por lo tanto la densidad de carga es
[ label {2.4.3} sigma = – frac {Q} {2 pi} cdot frac {h} {( rho ^ 2 + h ^ 2) ^ {3/2}}. ]
Esto puede también se escribirá
[ label {2.4.4} sigma = – frac {Q} {2 pi} cdot frac {h} {ξ ^ 3}, ]
donde (ξ ^ 2 = rho ^ 2 + h ^ 2 ), con Obvia interpretación geométrica.
Ejercicio : ¿Cuánta carga hay en la superficie de la placa dentro de un anillo limitado por radios ( rho ) y ( rho + d rho )? Integre esto de cero a infinito para mostrar que la carga total inducida en la placa es – (Q ).