( text {FIGURE II.3} )
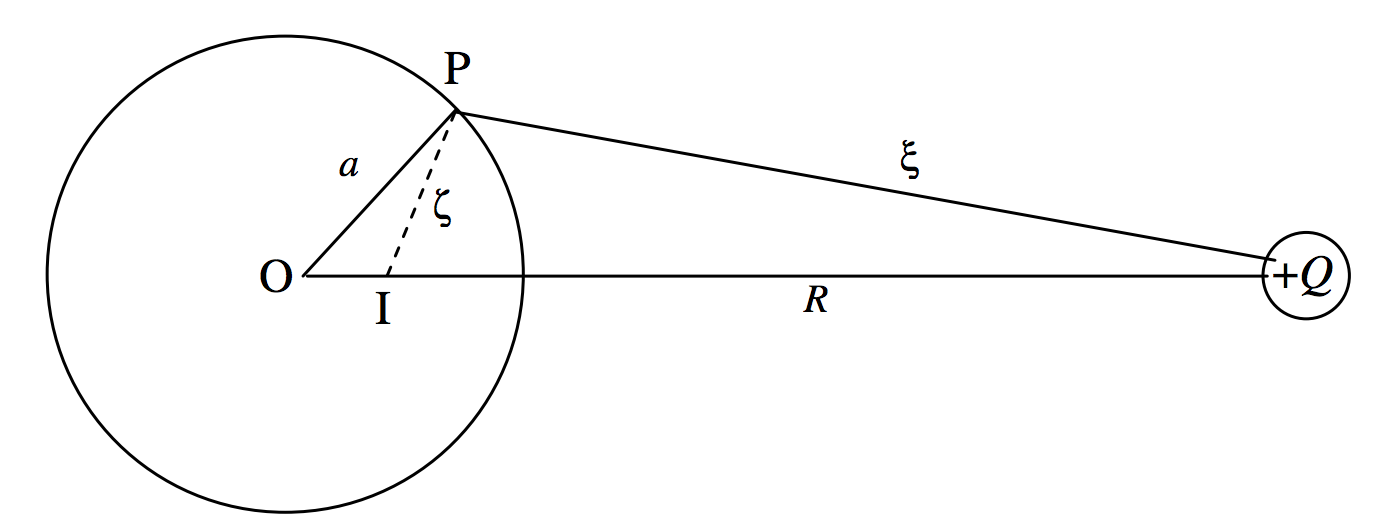
Una carga puntual + (Q ) está a una distancia (R ) de un esfera metálica de radio (a ). Vamos a tratar de calcular la densidad de carga superficial inducida en la superficie de la esfera, en función de la posición en la superficie. Debemos tener en cuenta que la superficie de la esfera es una superficie equipotencial, y tomaremos el potencial en la superficie como cero.
Primero construyamos un punto I tal que los triángulos OPI y PQO sean similares, con las longitudes mostradas en la Figura (II ). 3. La longitud OI es (a ^ 2 / R ). Entonces (R / ξ = a / ζ ), o
[ label {2.5.1} dfrac {1} {ξ} – dfrac {a / R} {ζ} = 0 ]
Esta relación entre las variables (ξ text {y} ζ ) es en efecto la ecuación a la esfera expresada en estas variables.
Ahora supongamos que, en lugar de la esfera metálica, tenemos (además de la carga + (Q ) a una distancia (R ) de O), una segunda carga puntual – (( a / R) Q text {at} I ). El lugar geométrico de los puntos donde el potencial es cero es donde
[ label {2.5.2} dfrac {Q} {4 pi epsilon_0} left ( dfrac {1} {ξ} – dfrac {a / R} {ζ} right) = 0 ]
Es decir, la superficie de nuestra esfera. Por lo tanto, para calcular el potencial, podemos reemplazar la esfera metálica por una imagen de (Q ) en (I ), esta imagen tiene una carga de (- (a / R ) Q ).
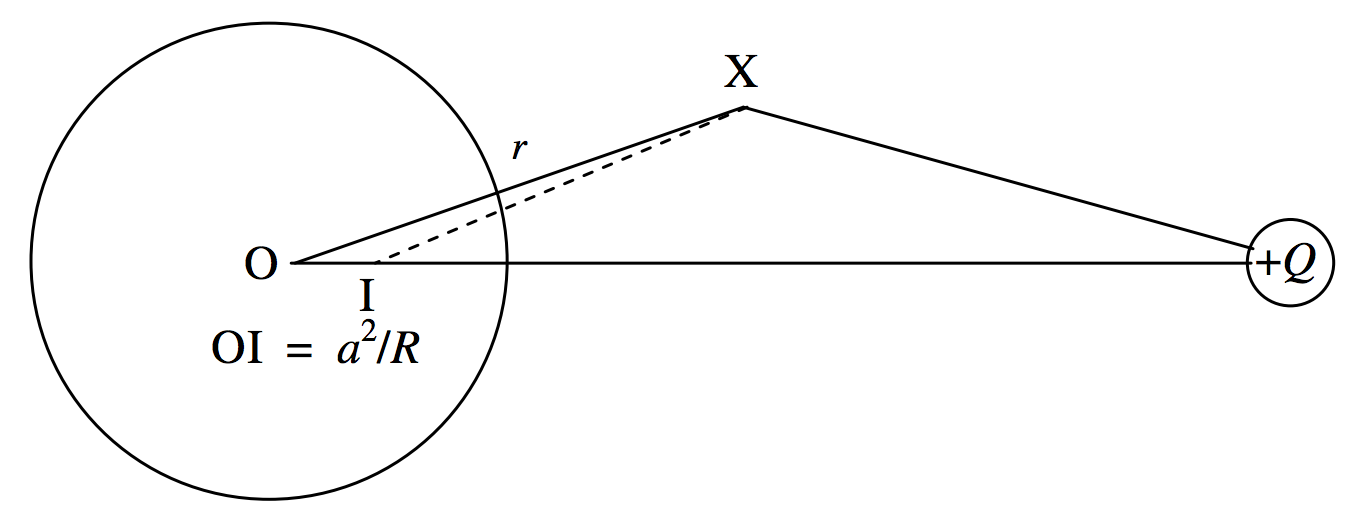
Tomemos la línea OQ como eje (z ) de un sistema de coordenadas. Sea (X ) un punto tal que OX = (r ) y el ángulo XOQ = (θ ). El potencial en P de una carga + (Q ) en (Q ) y una carga – ((a / R) Q ) en (I ) es (vea la Figura (II ). 4 )
( text {FIGURE II.4} )
[ nonumber V = dfrac {q} {4 pi epsilon_0} left ( dfrac {1} {(r ^ 2 + R ^ 2-2rR cos theta) ^ {1/2}} – dfrac {a / R} {(r ^ 2 + a ^ / R ^ 2 -2a ^ 2r cos theta / R) ^ {1/2}} right) ]
El campo E en la superficie de la esfera es ( −∂V / ∂r ) evaluado en (r = a ). El campo (D ) es ( epsilon_0 ) multiplicado por esto, y la densidad de carga superficial es igual a (D ). Después de un poco de paciencia y álgebra, obtenemos, para un punto (X ) en la superficie de la esfera
[ label {2.5.3} sigma = – dfrac {Q} {4 pi} dfrac {R ^ 2-a ^ 2} {a} cdot dfrac {1} {(XQ) ^ 3} ]