Suponga que el planeta Tierra es esférico y que tiene un pequeño imán o circuito de corriente en su centro. Por “pequeño” quiero decir pequeño comparado con el radio de la Tierra. Suponga que, a una gran distancia del imán o del circuito de corriente, la geometría del campo magnético es la misma que la de un campo eléctrico a una gran distancia de un dipolo simple. Es decir, la ecuación de las líneas de fuerza es
[r = a sin ^ 2 theta ]
y la ecuación diferencial a las líneas de fuerza es
[ frac {dr} {dθ} = frac {2r} {tan theta} ]
Muestre que el ángulo de caída (D ) en la latitud geomagnética (L ) viene dado por
[ tan D = 2 tan L label {3.10.1} ]
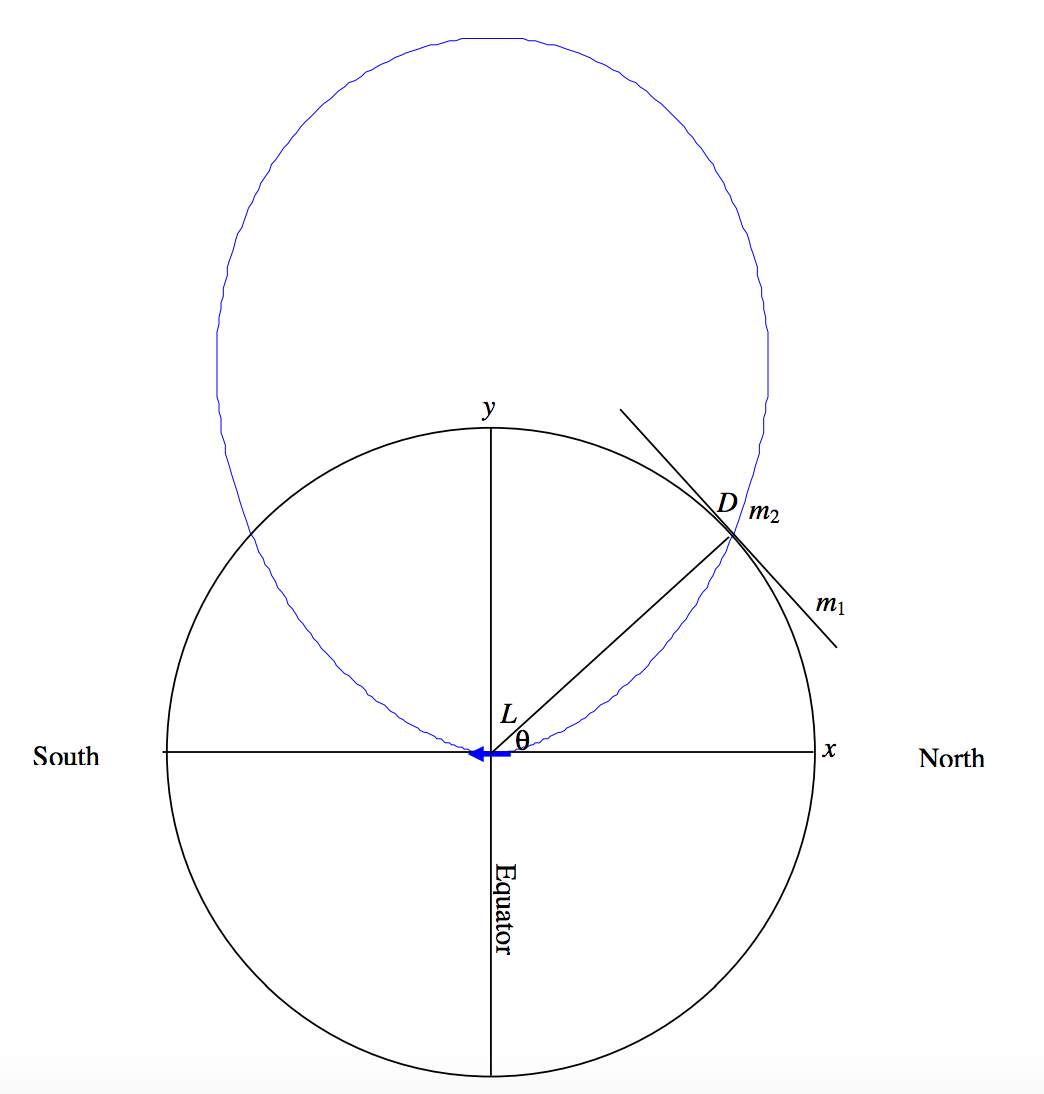
La geometría se muestra en la Figura (III ). 16.
El resultado es simple, y probablemente haya una forma más simple de obtenerlo que la que probé. Avíseme ( jtatum@uvic.ca ) si encuentra una manera más simple. Mientras tanto, aquí está mi solución.
Voy a tratar de encontrar la pendiente (m_1 ) de la tangente a la Tierra (es decir, del horizonte) y la pendiente (m_2 ) de la línea de fuerza. Entonces el ángulo D entre ellos estará dado por la ecuación (¡que espero sea bien conocida por la geometría de coordenadas!)
[ tan D = frac {m_1 -m_2} {1 + m_1m_2}. label {3.10.2} ]
El primero es fácil:
[m_1 = tan (90 ^ circ + theta) = – frac {1} { tan theta} label {3.10.3} ]
Para (m_2 ) queremos encontrar la pendiente de la línea de fuerza, cuya ecuación se da en coordenadas polares. Entonces, ¿cómo encuentras la pendiente de una curva cuya ecuación se da en coordenadas polares? Podemos hacerlo así:
[ begin {align} x & = r cos theta label {3.10.4}, \ y & = r sin theta label {3.10.5}, \ dx & = cos theta dr – r sin theta d theta label {3.10.6}, \ dy & = sin theta dr + r cos theta d theta. label {3.10.7} \ end {align} ]
De estos, obtenemos
[ frac {dy} {dx} = frac { sin theta frac {dr} {d theta} + r cos theta} { cos theta frac {dr} {d theta} -r sin theta}. label {3.10.8} ]
En nuestro caso particular, tenemos ( frac {dr} {d theta} = frac {2r} { tan theta} ) (ecuación 3.7.12), por lo que si sustituimos esto en la ecuación ( ref {3.10.8} ) pronto obtenemos
[m_2 = frac {3 sin theta cos theta} {3 cos ^ 2 theta -1}. Label {3.10.9} ]
Ahora ponga las ecuaciones ref {3.10.3} y ref {3.10.9} en la ecuación 3.10.2, y, después de un poco de álgebra, pronto obtendremos
[ tan D = frac {2} { tan theta} = 2 tan L. label {3.10.10} ]
Aquí hay otra pregunta. El campo magnético generalmente recibe el símbolo (B ). Demuestre que la intensidad del campo magnético (B (L) ) en la latitud geomagnética (L ) viene dada por
[B (L) = B (0) sqrt {1 + 3 sin ^ 2 L}, label {3.10.11} ]
donde (B (0) ) es la intensidad del campo en el ecuador. Esto significa que es dos veces más fuerte en los polos magnéticos que en el ecuador.
Comience con la ecuación 3.7.2, que proporciona el campo eléctrico en un punto distante en el ecuador de un dipolo eléctrico. Esa ecuación fue (E = frac {p} {4 pi epsilon_0 y ^ 3} ). En este caso, estamos tratando con un campo magnético y un dipolo magnético, por lo que reemplazaremos el campo eléctrico (E ) con un campo magnético (B ). Además, (p / (4π epsilon_0) ) es una combinación de cantidades eléctricas, y dado que solo nos interesa la geometría (es decir, cómo (B ) varía de ecuación a polo, simplemente escribamos (p / (4 pi epsilon_0) ) como (k ). Y tomaremos el radio de la Tierra como (R ), de modo que la ecuación 3.7.2 da el campo magnético en la superficie de la Tierra en el ecuador como
[B (0) = frac {k} {R ^ 3}. label {3.10.12} ]
En una veta similar, las ecuaciones 3.7.10 para los componentes radiales y transversales del campo en la latitud geomagnética (L ) (que es 90º – (θ )) se convierten en
[B_r (L) = frac {2k sin L} {R ^ 3} quad text {y} quad B _ { theta} (L) = frac {k cos L} { R ^ 3}. label {3.10.13a, b} ]
Y desde (B = sqrt {B_r ^ 2 + B _ { theta} ^ 2} ) el resultado sigue inmediatamente.