Cuando un nuevo compuesto químico, como un posible nuevo producto farmacéutico, se sintetiza en el laboratorio o se aísla de una fuente natural, los químicos determinan su composición elemental, su fórmula empírica y su estructura para comprender sus propiedades. Esta sección se enfoca en cómo determinar la fórmula empírica de un compuesto y luego usarla para determinar la fórmula molecular si se conoce la masa molar del compuesto.
Fórmula y pesos moleculares
El peso de fórmula de una sustancia es la suma de los pesos atómicos de cada átomo en su fórmula química . Por ejemplo, el agua (H 2 O) tiene un peso de fórmula de:
[2 veces (1.0079 ; amu) + 1 veces (15.9994 ; amu) = 18.01528 ; amu ]
Si una sustancia existe como moléculas discretas (como con los átomos que están unidos químicamente juntos), entonces la fórmula química es la fórmula molecular [ 19459018], y el peso de la fórmula es el peso molecular . Por ejemplo, el carbono, el hidrógeno y el oxígeno pueden unirse químicamente para formar una molécula del azúcar glucosa con la fórmula química y molecular de C 6 H 12 O [ 19459019] 6 . El peso de la fórmula y el peso molecular de la glucosa es así:
Las sustancias iónicas no están unidas químicamente y no existen como moléculas discretas. Sin embargo, se asocian en proporciones discretas de iones. Por lo tanto, podemos describir sus pesos de fórmula, pero no sus pesos moleculares . La sal de mesa (NaCl), por ejemplo, tiene un peso de fórmula de:
[23.0 ; amu + 35.5 ; amu = 58.5 ; amu ]
Composición porcentual a partir de fórmulas
En algunos tipos de análisis es importante conocer el porcentaje en masa de cada tipo de elemento en un compuesto. La ley de proporciones definidas establece que un compuesto químico siempre contiene la misma proporción de elementos en masa; es decir, la composición porcentual (el porcentaje de cada elemento presente en una sustancia pura) es constante (aunque hay excepciones a esta ley). Tomemos, por ejemplo, metano ( (CH_4 )) con una fórmula y peso molecular:
[1 veces (12.011 ; amu) + 4 veces (1.008) = 16.043 ; amu ]
los porcentajes relativos (en masa) de carbono e hidrógeno son
[% C = dfrac {1 veces (12.011 ; amu)} {16.043 amu} = 0.749 = 74.9 % ]
[% H = dfrac {4 veces (1.008 ; amu)} {16.043 ; amu} = 0.251 = 25.1 % ]
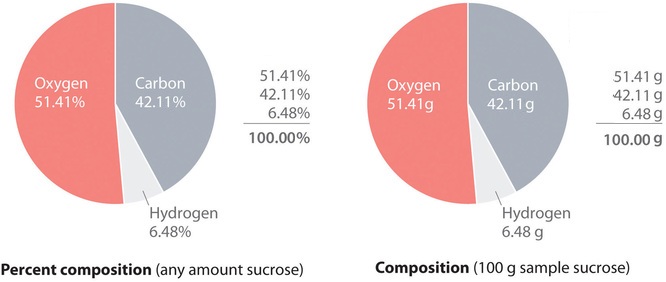
Un ejemplo más complejo es la sacarosa (azúcar de mesa) que contiene 42.11% de carbono, 6.48% de hidrógeno y 51.41% de oxígeno en masa. Esto significa que 100.00 g de sacarosa siempre contienen 42.11 g de carbono, 6.48 g de hidrógeno y 51.41 g de oxígeno. Primero se usa la fórmula molecular de sacarosa (C 12 H 22 O 11 ) para calcular el porcentaje de masa de los elementos componentes; el porcentaje de masa se puede usar para determinar una fórmula empírica .
Según su fórmula molecular, cada molécula de sacarosa contiene 12 átomos de carbono, 22 átomos de hidrógeno y 11 átomos de oxígeno. Por lo tanto, un mol de moléculas de sacarosa contiene 12 mol de átomos de carbono, 22 mol de átomos de hidrógeno y 11 mol de átomos de oxígeno. Esta información se puede utilizar para calcular la masa de cada elemento en 1 mol de sacarosa, lo que da la masa molar de sacarosa. Estas masas se pueden usar para calcular el porcentaje de composición de sacarosa. A tres decimales, los cálculos son los siguientes:
[ text {masa de C / mol de sacarosa} = 12 , mol , C times {12.011 , g , C over 1 , mol , C} = 144.132 , g , C label {3.1.1a} ]
[ text {masa de H / mol de sacarosa} = 22 , mol , H times {1.008 , g , H over 1 , mol , H} = 22.176 , g , C label {3.1.1b} ]
[ text {masa de O / mol de sacarosa} = 11 , mol , O times {15.999 , g , O over 1 , mol , O} = 175.989 , g , O label {3.1.1c} ]
Así, 1 mol de sacarosa tiene una masa de 342.297 g; tenga en cuenta que más de la mitad de la masa (175.989 g) es oxígeno, y casi la mitad de la masa (144.132 g) es carbono.
El porcentaje de masa de cada elemento en sacarosa es la masa del elemento presente en 1 mol de sacarosa dividido por la masa molar de sacarosa, multiplicado por 100 para dar un porcentaje. El resultado se muestra con dos decimales:
[ text {mass% C en sacarosa} = { text {masa de C / mol sacarosa} over text {masa molar de sacarosa}} times100 = {144.132 , g , C over 342.297 , g / mol} veces 100 = 42.12 % ]
[ text {masa% H en sacarosa} = { text {masa de H / mol sacarosa} over text {masa molar de sacarosa}} times100 = {22.176 , g , H over 342.297 , g / mol} veces 100 = 6.48 % ]
[ text {mass% O en sacarosa} = { text {masa de O / mol sacarosa} over text {masa molar de sacarosa}} times100 = {175.989 , g , O over 342.297 , g / mol} times 100 = 51.41 % ]
Esto se puede verificar verificando que la suma de los porcentajes de todos los elementos en el compuesto es 100%:
[42.12 % + 6.48 % + 51.41 % = 100.01 % ]
Si la suma no es 100%, se ha cometido un error en los cálculos. (Sin embargo, redondear al número correcto de decimales puede hacer que el total sea ligeramente diferente del 100%.) Por lo tanto, 100.00 g de sacarosa contienen 42.12 g de carbono, 6.48 g de hidrógeno y 51.41 g de oxígeno; a dos decimales, la composición porcentual de sacarosa es de hecho 42.12% de carbono, 6.48% de hidrógeno y 51.41% de oxígeno.
También es posible calcular porcentajes de masa utilizando masas atómicas y masas moleculares, con unidades de masa atómica. Debido a que la respuesta es una relación, expresada como un porcentaje, las unidades de masa cancelan si son gramos (usando masas molares) o unidades de masa atómica (usando masas atómicas y moleculares).
Determinación de la fórmula empírica de la penicilina
Así como la fórmula empírica de una sustancia puede usarse para determinar su composición porcentual, la composición porcentual de una muestra puede usarse para determinar su fórmula empírica, que luego puede usarse para determinar su fórmula molecular. Tal procedimiento se usó realmente para determinar las fórmulas empíricas y moleculares del primer antibiótico que se descubrió: la penicilina.
Los antibióticos son compuestos químicos que matan selectivamente microorganismos, muchos de los cuales causan enfermedades. Aunque los antibióticos a menudo se dan por sentado hoy, la penicilina se descubrió hace solo 80 años. El desarrollo posterior de una amplia gama de otros antibióticos para tratar muchas enfermedades comunes ha contribuido en gran medida al aumento sustancial de la esperanza de vida en los últimos 50 años. El descubrimiento de la penicilina es una historia de detectives histórica en la que el uso de porcentajes en masa para determinar fórmulas empíricas desempeñó un papel clave.
En 1928, Alexander Fleming, un joven microbiólogo de la Universidad de Londres, estaba trabajando con una bacteria común que causa forúnculos y otras infecciones como el envenenamiento de la sangre. Para el estudio de laboratorio, las bacterias se cultivan comúnmente en la superficie de un gel que contiene nutrientes en pequeños platos de cultivo planos. Un día, Fleming notó que una de sus culturas estaba contaminada por un moho verde azulado similar al moho que se encuentra en el pan o la fruta en mal estado. Tales accidentes son bastante comunes, y la mayoría de los trabajadores de laboratorio simplemente habrían desechado los cultivos. Sin embargo, Fleming notó que las bacterias estaban creciendo en todas partes en el gel, excepto cerca del molde contaminante (parte (a) en Figura ( PageIndex {2} ) ), e hizo la hipótesis de que el moho debe estar produciendo una sustancia que mató a la bacteria o impidió su crecimiento. Para probar esta hipótesis, hizo crecer el moho en un líquido y luego filtró el líquido y lo agregó a varios cultivos de bacterias. El líquido mató no solo a la bacteria que Fleming había estado estudiando originalmente, sino también a una amplia gama de otras bacterias que causan enfermedades. Debido a que el molde era un miembro de la familia Penicillium (llamado así por sus ramas en forma de lápiz bajo el microscopio) (parte (b) en Figura ( PageIndex {2} ) ), Fleming llamó al activo ingrediente en el caldo de penicilina.

Aunque Fleming no pudo aislar la penicilina en forma pura, la importancia médica de su descubrimiento estimuló a los investigadores de otros laboratorios. Finalmente, en 1940, dos químicos de la Universidad de Oxford, Howard Florey (1898–1968) y Ernst Chain (1906–1979), pudieron aislar un producto activo, al que llamaron penicilina G. En tres años, la penicilina G estaba muy extendida. se usa para tratar neumonía, gangrena, gonorrea y otras enfermedades, y su uso aumentó en gran medida la tasa de supervivencia de los soldados heridos en la Segunda Guerra Mundial. Como resultado de su trabajo, Fleming, Florey y Chain compartieron el Premio Nobel de Medicina en 1945.
Tan pronto como lograron aislar la penicilina G pura, Florey y Chain sometieron el compuesto a un procedimiento llamado análisis de combustión (descrito más adelante en esta sección) para determinar qué elementos estaban presentes y en qué cantidades. Los resultados de tales análisis generalmente se informan como porcentajes de masa. Descubrieron que una muestra típica de penicilina G contiene 53.9% de carbono, 4.8% de hidrógeno, 7.9% de nitrógeno, 9.0% de azufre y 6.5% de sodio en masa. La suma de estos números es solo 82.1%, en lugar de 100.0%, lo que implica que debe haber uno o más elementos adicionales. Un candidato razonable es el oxígeno, que es un componente común de los compuestos que contienen carbono e hidrógeno; no asuma que la masa “faltante” siempre se debe al oxígeno. Podría ser cualquier otro elemento. Sin embargo, por razones técnicas, es difícil analizar el oxígeno directamente. Suponiendo que toda la masa faltante se deba al oxígeno, entonces la penicilina G contiene (100.0% – 82.1%) = 17.9% de oxígeno. A partir de estos porcentajes de masa, se puede determinar la fórmula empírica y, finalmente, la fórmula molecular del compuesto.
Para determinar la fórmula empírica a partir de los porcentajes en masa de los elementos en un compuesto como la penicilina G, los porcentajes en masa deben convertirse a números relativos de átomos. Por conveniencia, suponga una muestra de 100.0 g del compuesto, aunque los tamaños de las muestras utilizadas para los análisis son generalmente mucho más pequeños, generalmente en miligramos. Esta suposición simplifica la aritmética porque un 53.9% de porcentaje en masa de carbono corresponde a 53.9 g de carbono en una muestra de 100.0 g de penicilina G; asimismo, 4.8% de hidrógeno corresponde a 4.8 g de hidrógeno en 100.0 g de penicilina G; y así sucesivamente para los otros elementos. Luego, cada masa se divide por la masa molar del elemento para determinar cuántos moles de cada elemento están presentes en la muestra de 100.0 g:
[{mass , (g) over molar , , mass , , (g / mol)} = (g) left ({mol over g} right) = mol label {3.3.2a} ]
[53.9 , g , C left ({1 , mol , C over 12.011 , g , C} right) = 4.49 , mol , C label {3.3.2b } ]
[4.8 , g , H left ({1 , mol , H over 1.008 g , H} right) = 4.8 , mol , H label {3.3.2c} ]
[7.9 , g , N left ({1 , mol , N over 14.007 , g , N} right) = 0.56 , mol , N label {3.3.2d } ]
[9 , g , S left ({1 , mol , S over 32.065 , g , S} right) = 0.28 , mol , S label {3.3.2e } ]
[6.5 , g , Na left ({1 , mol , Na over 22.990 , g , Na} right) = 0.28 , mol , Na label {3.3.2f } ]
Así, 100,0 g de penicilina G contienen 4,49 moles de carbono, 4,8 moles de hidrógeno, 0,56 moles de nitrógeno, 0,28 moles de azufre, 0,28 moles de sodio y 1,12 moles de oxígeno (suponiendo que toda la masa faltante sea oxígeno) . El número de cifras significativas en el número de moles de elementos varía entre dos y tres porque algunos de los datos analíticos se informaron a solo dos cifras significativas.
Estos resultados dan las proporciones de los moles de los diversos elementos en la muestra (4,49 moles de carbono a 4,8 moles de hidrógeno a 0,56 moles de nitrógeno, etc.), pero no son las proporciones de números enteros necesarios para La fórmula empírica: la fórmula empírica expresa los números relativos de átomos en los números enteros más pequeños posibles. Para obtener números enteros, divida el número de moles de todos los elementos de la muestra por el número de moles del elemento presente en la cantidad relativa más baja, que en este ejemplo es azufre o sodio. Los resultados serán los subíndices de los elementos en la fórmula empírica. Para dos cifras significativas, los resultados son los siguientes:
[C: {4.49 over 0.28} = 16 , , , , , H: {4.8 over 0.28} = 17 , , , , , N: {0.56 más de 0.28} = 2.0 label {3.3.3a} ]
[S: {0.28 over 0.28} = 1.0 , , , , , Na: {0.28 over 0.28} = 1.0 , , , , , O: {1.12 más de 0.28} = 4.0 label {3.3.3b} ]
La fórmula empírica de la penicilina G es, por lo tanto, C 16 H 17 N 2 NaO 4 S. Otros experimentos han demostrado que la penicilina G es en realidad un compuesto iónico que contiene Na + cationes y [C 16 H 17 N 2 O 4 [ 19459020] S] – aniones en una relación 1: 1. La estructura compleja de la penicilina G ( Figura ( PageIndex {3} ) ) no se determinó hasta 1948.

En algunos casos, uno o más de los subíndices en una fórmula calculada usando este procedimiento pueden no ser enteros. ¿Significa esto que el compuesto de interés contiene un número no integral de átomos? No; Los errores de redondeo en los cálculos, así como los errores experimentales en los datos, pueden dar como resultado relaciones no integrales. Cuando esto sucede, se debe ejercer juicio al interpretar los resultados, como se ilustra en el Ejemplo 6. En particular, las proporciones de 1.50, 1.33 o 1.25 sugieren que debe multiplicar todos los subíndices en la fórmula por 2, 3 o 4, respectivamente. Solo si la relación está dentro del 5% de un valor integral, se debe considerar redondear al número entero más cercano.
De la fórmula empírica a la fórmula molecular
La fórmula empírica da solo el número relativo de átomos en una sustancia en la proporción más pequeña posible. Para una sustancia covalente, los químicos suelen estar más interesados en la fórmula molecular, que proporciona el número real de átomos de cada tipo presente por molécula. Sin información adicional, sin embargo, es imposible saber si la fórmula de la penicilina G, por ejemplo, es C 16 H 17 N 2 NaO 4 S o un múltiplo integral, como C 32 H 34 N 4 Na 2 O 8 [ 19459020] S 2 , C 48 H 51 N 6 Na 3 O 12 ] S 3 , o (C 16 H 17 N 2 NaO 4 S) n , donde n es un número entero. (La estructura real de la penicilina G se muestra en Figura ( PageIndex {3} ) ).
Considera la glucosa, el azúcar que circula en nuestra sangre para proporcionar combustible para el cuerpo y el cerebro. Los resultados del análisis de combustión de glucosa informan que la glucosa contiene 39,68% de carbono y 6,58% de hidrógeno. Debido a que la combustión ocurre en presencia de oxígeno, es imposible determinar directamente el porcentaje de oxígeno en un compuesto mediante el análisis de combustión; Se necesitan otros métodos más complejos. Suponiendo que el porcentaje restante se debe al oxígeno, la glucosa contendría 53.79% de oxígeno. Por lo tanto, una muestra de 100.0 g de glucosa contendría 39.68 g de carbono, 6.58 g de hidrógeno y 53.79 g de oxígeno. Para calcular el número de moles de cada elemento en la muestra de 100.0 g, divida la masa de cada elemento por su masa molar:
[moles , C = 39.68 , g , C times {1 , mol , C over 12.011 , g , C} = 3.304 , mol , C label {3.3. 4a} ]
[moles , H = 6.58 , g , H times {1 , mol , H over 1.0079 , g , H} = 6.53 , mol , H label {3.3. 4b} ]
[moles , O = 53.79 , g , O times {1 , mol , O over 15.9994 , g , O} = 3.362 , mol , O label {3.3. 4c} ]
Una vez más, los subíndices de los elementos en la fórmula empírica se encuentran dividiendo el número de moles de cada elemento por el número de moles del elemento presente en la cantidad más pequeña:
[C: {3.304 over 3.304} = 1.000 , , , , H: {6.53 over 3.304} = 1.98 , , , , O: {3.362 over 3.304} = 1.018 ]
La relación oxígeno: carbono es 1.018, o aproximadamente 1, y la relación hidrógeno: carbono es aproximadamente 2. La fórmula empírica de glucosa es, por lo tanto, CH 2 O, pero ¿cuál es su fórmula molecular?
Muchos compuestos conocidos tienen la fórmula empírica CH 2 O, incluido el formaldehído, que se utiliza para preservar especímenes biológicos y tiene propiedades que son muy diferentes del azúcar que circula en la sangre. En este punto, no se puede saber si la glucosa es CH 2 O, C 2 H 4 O 2 , o cualquier otro ( CH 2 O) n . Sin embargo, la masa molar de glucosa determinada experimentalmente (180 g / mol) puede usarse para resolver este dilema.
Primero, calcule la masa de la fórmula, la masa molar de la unidad de fórmula, que es la suma de las masas atómicas de los elementos en la fórmula empírica multiplicada por sus respectivos subíndices. Para glucosa,
[ text {fórmula masa de} CH_2O = left [1 , mol C left ({12.011 , g over 1 , mol , C} right) right] + left [ 2 , mol , H left ({1.0079 , g over 1 , mol , H} right) right] + left [1 , mole , O left ({15.5994 , mol , O over 1 , mol , O} right) right] = 30.026 g label {3.3.5} ]
Esto es mucho más pequeño que la masa molar observada de 180 g / mol.
Segundo, determine el número de unidades de fórmula por mol. Para la glucosa, calcule el número de unidades (CH 2 O), es decir, la n en (CH 2 O) n , dividiendo la masa molar de glucosa por la masa de fórmula de CH 2 O:
[n = {180 , g over 30.026 , g / CH_2O} = 5.99 aprox 6 CH_2O , text {unidades de fórmula} label {3.3.6} ]
Cada glucosa contiene seis unidades de fórmula CH 2 O, que proporciona una fórmula molecular para glucosa de (CH 2 O) 6 , que es más común escrito como C 6 H 12 O 6 . Las estructuras moleculares de formaldehído y glucosa, que tienen la fórmula empírica CH 2 O, se muestran en Figura ( PageIndex {4} ).

Summary
The empirical formula of a substance can be calculated from its percent composition, and the molecular formula can be determined from the empirical formula and the compound’s molar mass. The empirical formula of a substance can be calculated from the experimentally determined percent composition, the percentage of each element present in a pure substance by mass. In many cases, these percentages can be determined by combustion analysis. If the molar mass of the compound is known, the molecular formula can be determined from the empirical formula.
Contributors
-
Mike Blaber ( Florida State University )