Como se puede esperar del título de esta sección, esta será la sección más difícil y complicada de este capítulo hasta ahora. Nuestro objetivo será calcular el campo y el potencial que rodea a un dipolo simple.
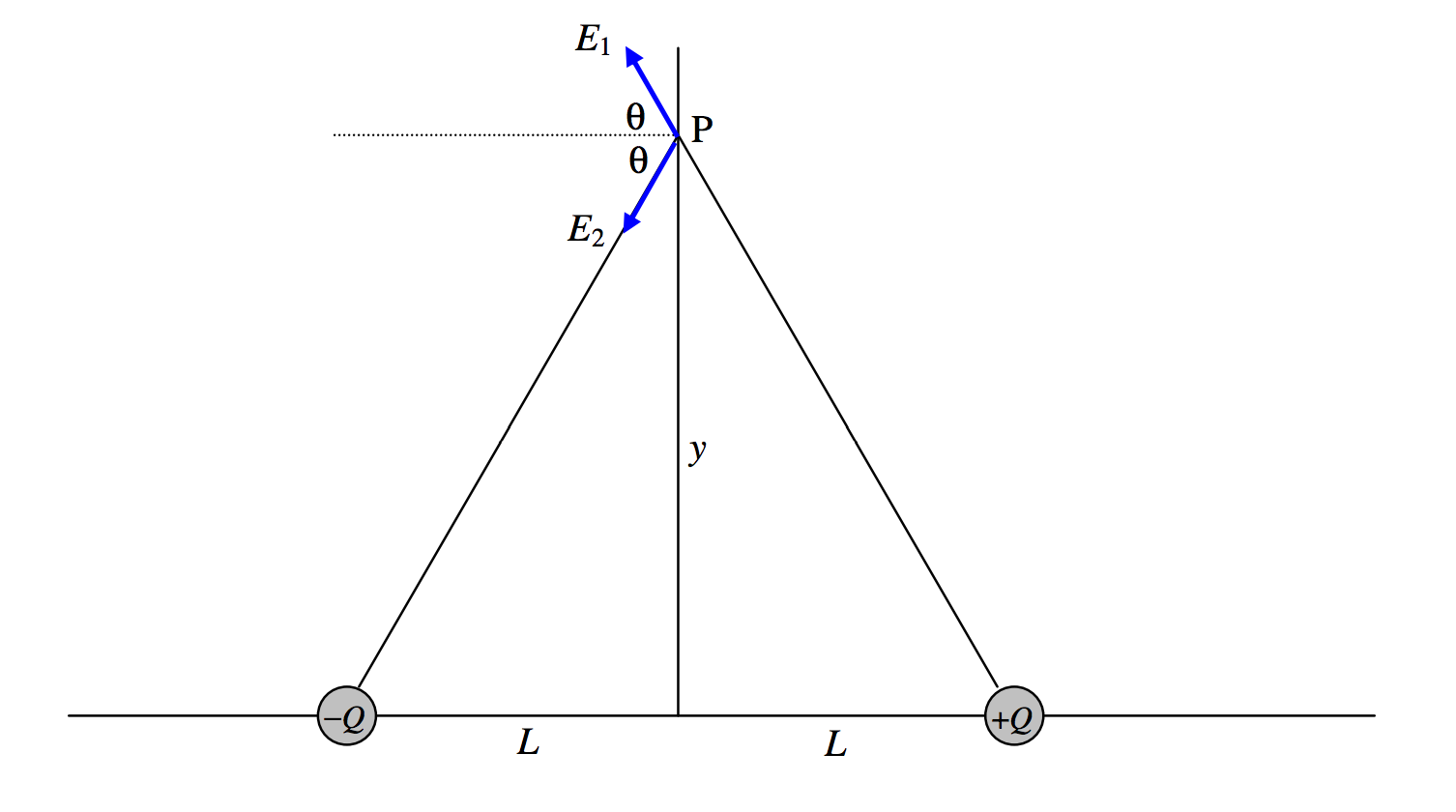
Un dipolo simple es un sistema que consta de dos cargas, (+ Q text {y} −Q ), separadas por una distancia (2L ). El momento dipolar de este sistema es solo (p = 2QL ). Supondremos que el dipolo se encuentra a lo largo del eje x , con la carga negativa en (x = −L ) y la carga positiva en (x = + L ). Ver Figura (III ). 5.
( text {FIGURA III.5} )
Primero calculemos el campo eléctrico en un punto P a una distancia (y ) a lo largo del eje (y ). Se acordará, creo, que está dirigido hacia la izquierda y es igual a
[E_1 cos theta + E_2 cos theta, text {where} E_1 = E_2 = dfrac {Q} {4 pi epsilon_0 (L ^ 2 + y ^ 2)} text { y} cos theta = dfrac {L} {(L ^ 2 + y ^ 2) ^ {1/2}}. nonumber ]
Por lo tanto
[E = dfrac {2QL} {4 pi epsilon_0 (L ^ 2 + y ^ 2) ^ {3/2}} = dfrac {p} {4 pi epsilon_0 (L ^ 2 + y ^ 2) ^ {3/2}}. label {3.7.1} ]
Para grandes (y ) esto se convierte en
[ label {3.7.2} E = dfrac {p} {4 pi epsilon_0y ^ 3}. ]
Es decir, el campo se cae como el cubo de la distancia.
Para encontrar el campo en el eje (x ) -, consulte la Figura (III ). 6.
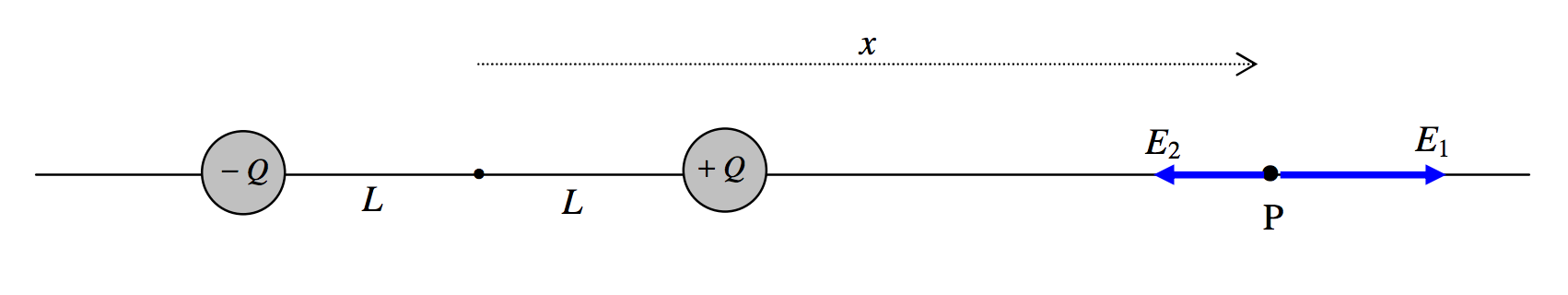
( text {FIGURA III.6} )
Se acordará, creo, que el campo está dirigido hacia la derecha y es igual a
[ label {3.7.3} E = E_1-E_2 = dfrac {Q} {4 pi epsilon_0} left ( dfrac {1} {(xL) ^ 2} – dfrac {1 } {(x + L) ^ 2} right). ]
Esto se puede escribir ( dfrac {Q} {4 pi epsilon_0x ^ 2} left ( dfrac {1} {(1-L / x) ^ 2} – dfrac {1} {( 1 + L / x) ^ 2} right) ), y en la expansión de esto por el teorema binomial , descuidando los términos de orden ((L / x) ^ 2 ) y más pequeños, ver que en general x el campo es
[ label {3.7.4} E = dfrac {2p} {4 pi epsilon_0x ^ 3}. ]
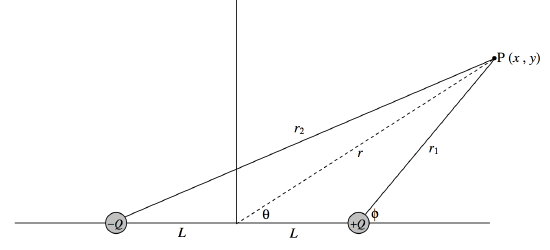
Ahora para el campo en un punto P que no está ni en el eje ( (x ) – eje) ni en el ecuador ( (y ) – eje) del dipolo. Ver Figura (III ). 7.
( text {FIGURA III.7} )
Probablemente se acordará que no sería particularmente difícil escribir expresiones para las contribuciones al campo en P de cada uno de los dos cargos por turno. Entonces comienza la parte difícil; Las dos contribuciones al campo están en direcciones diferentes e incómodas, y agregarlas vectorialmente será un poco dolor de cabeza.
Es mucho más fácil calcular el potencial en P, ya que las dos contribuciones al potencial pueden agregarse como escalares. Luego podemos encontrar los componentes x y y del campo calculando (∂V / ∂x ) y (∂V / ∂y ).
Así
[V = dfrac {Q} {4 pi epsilon_0} left ( dfrac {1} { {(xL) ^ 2 + y ^ 2 } ^ {1/2}} – dfrac {1} { {(x + L) ^ 2 + y ^ 2 } ^ {1/2}} right). label {3.7.5} ]
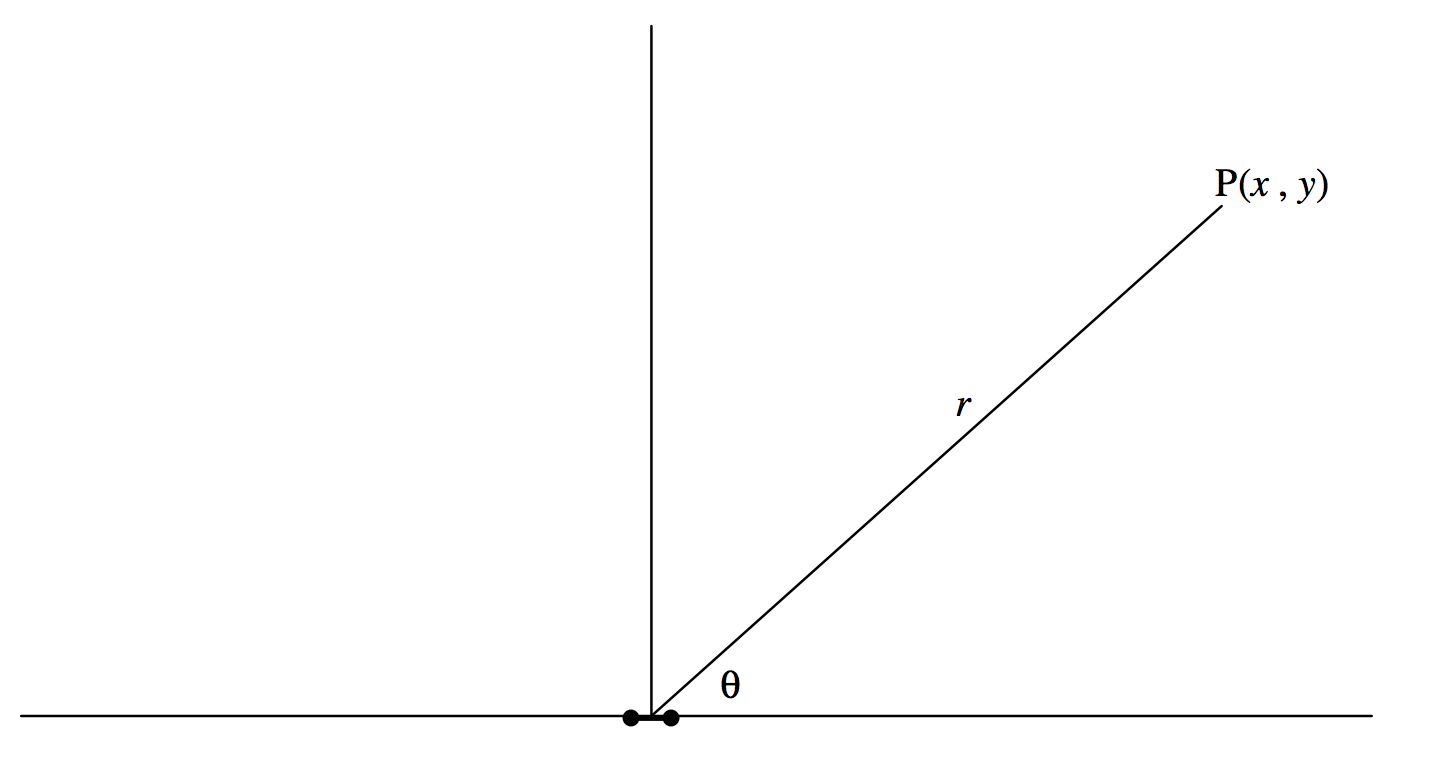
Para empezar, voy a investigar el potencial y el campo a una gran distancia del dipolo, aunque volveré más tarde a la vecindad cercana.
A grandes distancias desde un dipolo pequeño (ver Figura (III ). 8), podemos escribir, (r ^ 2 = x ^ 2 + y ^ 2 ), [19459002 ]
( text {FIGURA III.8} )
y, con (L ^ 2 << r ^ 2 ), la expresión 3.7.5 para el potencial en P se convierte en
[V = dfrac {Q} {4 pi epsilon_0} left ( dfrac {1} {(r ^ 2-2Lx) ^ {1/2}} – dfrac {1} {( r ^ 2 + 2Lx) ^ {1/2}} right) = dfrac {Q} {4 pi epsilon_0 r} left ((1-2Lx / r ^ 2) ^ {- 1/2} – (1 + 2Lx / r ^ 2) ^ {- 1/2} right). Nonumber ]
Cuando esto se expande mediante el teorema binomial, encontramos, para ordenar L / r , que el potencial se puede escribir de cualquiera de las siguientes formas equivalentes:
[ label {3.7.6} V = dfrac {2QLx} {4 pi epsilon_0 r ^ 3} = dfrac {px} {4 pi epsilon_0 r ^ 3} = dfrac {p cos theta} {4 pi epsilon_0 r ^ 2} = dfrac { textbf {p} cdot textbf {r}} {4 pi epsilon_0 r ^ 3}. ]
Así, los equipotenciales son de la forma
[ label {3.7.7} r ^ 2 = c cos theta, ]
donde
[ label {3.7.8} c = dfrac {p} {4 pi epsilon_0 V}. ]
Ahora, teniendo en cuenta que (r ^ 2 + x ^ 2 + y ^ 2 ), podemos diferenciar (V = dfrac {px} {4 pi epsilon_0 r ^ 3} ) con respecto a (x ) y (y ) para encontrar los componentes (x ) – y (y ) – del campo. Así encontramos que
[ label {3.7.9} E_x = dfrac {p} {4 pi epsilon_0} left ( dfrac {3x ^ 2-r ^ 2} {r ^ 5} right) text {y} E_y = dfrac {pxy} {4 pi epsilon r ^ 5}. ]
También podemos utilizar coordenadas polares para encontrar los componentes radiales y transversales de (E_r = – dfrac {∂V} {∂r} text {y} E_ theta = – dfrac {1} {r} dfrac {∂V} {∂ theta} text {junto con} V = dfrac {p cos theta} {4 pi epsilon_0 r ^ 2} ) para obtener
[ label {3.7.10} E_r = dfrac {2p cos theta} {4 pi epsilon_0 r ^ 3}, quad E_ theta = dfrac {p sin theta} { 4 pi epsilon_0 r ^ 3} text {y} E = dfrac {p} {4 pi epsilon_0 r ^ 3} sqrt {1 + 3 cos ^ 2 theta}. ]
El ángulo que ( textbf {E} ) forma con el eje del dipolo en el punto ((r, θ) ) es (θ + tan ^ {- 1} dfrac {1 } {2} tan theta ).
Para aquellos que disfrutan el cálculo vectorial, también podemos decir ( textbf {E} = – dfrac {1} {4 pi epsilon_0} nabla left ( dfrac { textbf {p} cdot textbf {r}} {r ^ 3} right) ), de donde, después de un poco de álgebra y bastante cálculo vectorial, encontramos
[ label {3.7.11} textbf {E} = dfrac {1} {4 pi epsilon_0} left ( dfrac {3 ( textbf {p} cdot textbf {r} ) textbf {r}} {r ^ 5} – dfrac { textbf {p}} {r ^ 3} right). ]
Esta ecuación contiene toda la información que es probable que deseemos, pero espero que la mayoría de los lectores prefieran las formas rectangulares y polares más explícitas de las ecuaciones ref {3.7.9} y ref {3.7.10}.
La ecuación ref {3.7.7} da la ecuación a los equipotenciales. La ecuación de las líneas de fuerza se puede encontrar de la siguiente manera. En referencia a la Figura (III ). 9, vemos que la ecuación diferencial de las líneas de fuerza es
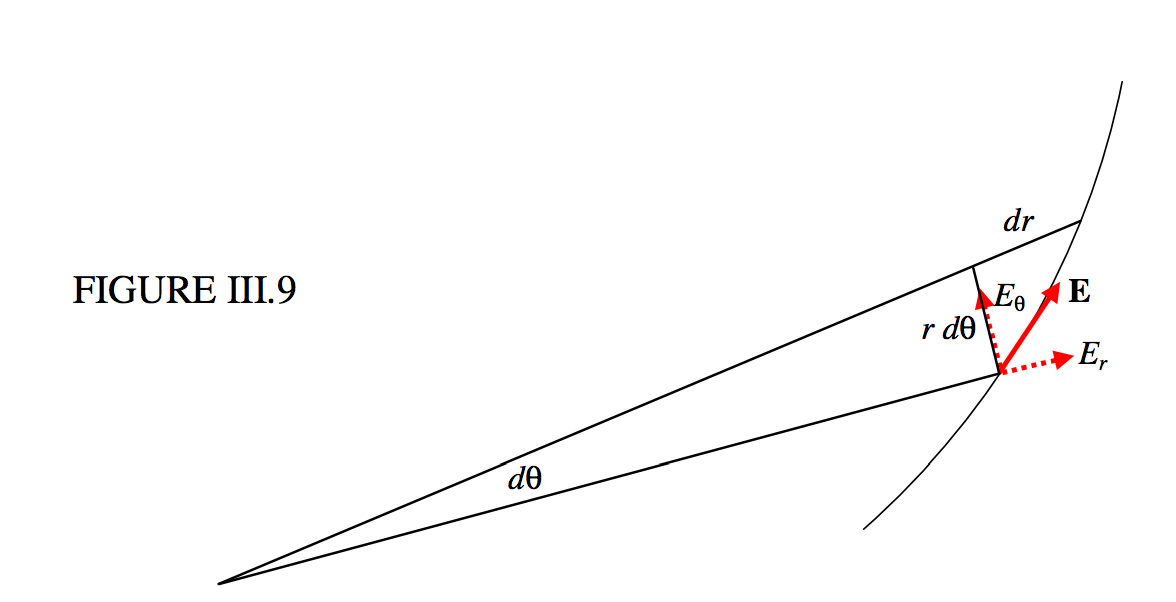
( text {FIGURA III.9} )
[ label {3.7.12} r dfrac {d theta} {dr} = dfrac {E_ theta} {E_r} = dfrac { sin theta} {2 cos theta} = dfrac {1} {2} tan theta, ]
que, al integrarse, se convierte en
[ label {3.7.13} r = a sin ^ 2 theta. ]
Tenga en cuenta que las ecuaciones (r ^ 2 = c cos θ ) (para los equipotenciales) y (r = a sin ^ 2 theta ) (para las líneas de fuerza) son trayectorias ortogonales, y cualquiera puede derivarse de la otra. Por lo tanto, dado que la ecuación diferencial de las líneas de fuerza es (r dfrac {d theta} {dr} = dfrac {1} {2} tan theta ) con solución (r = a sin ^ 2 theta ), la ecuación diferencial de las trayectorias ortogonales (es decir, los equipotenciales) es (- dfrac {1} {r} dfrac {dr} {d theta} = dfrac {1} {2} tan theta ), con la solución (r ^ 2 = c cos theta ).
En la Figura (III ). 10, se supone que hay un pequeño dipolo situado en el origen. La unidad de longitud es (L ), la mitad de la longitud del dipolo. He dibujado ocho líneas de campo eléctrico (continuo), correspondientes a a = 25, 50, 100, 200, 400, 800, 1600, 3200. Si r se expresa en unidades de (L ), y si (V ) se expresa en unidades de ( dfrac {Q} {4 pi epsilon_0 L} ), las ecuaciones ref {3.7.7} y ref {3.7 .8} para los equipotenciales se pueden escribir, (r = sqrt { dfrac {2 cos theta} {V}} ), y he dibujado siete equipotenciales (con guiones) para (V ) = 0.0001 , 0.0002, 0.0004, 0.0008, 0.0016, 0.0032, 0.0064. Se notará en la ecuación ref {3.7.9a}, y también es evidente en la figura (III ). 10, que (E_x ) es cero para ( theta = 54 ^ circ , 44 ‘ ).
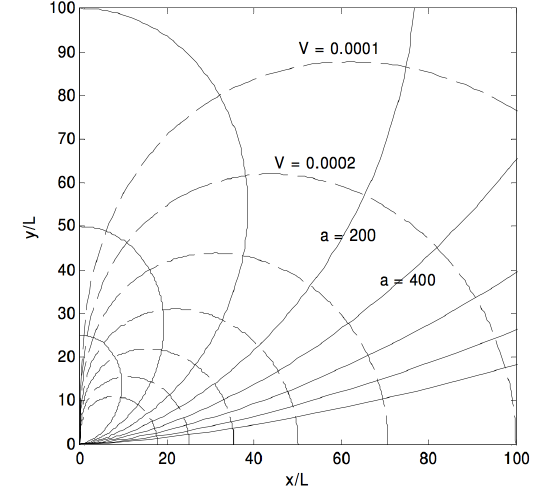
( text {FIGURA III.10} )
Al final de este capítulo agrego un ejercicio (geofísico) en la geometría del campo a una gran distancia de un dipolo pequeño.
Equipotenciales cerca del dipolo
Estas son, entonces, las líneas de campo y los equipotenciales a una gran distancia del dipolo. Llegamos a estas ecuaciones y gráficos expandiendo la ecuación ref {3.7.5} binomialmente, y descuidando los términos de orden superior a (L / r ). Ahora miramos cerca al dipolo, donde no podemos hacer tal aproximación. Consulte la Figura (III ) .7.
Podemos escribir la ecuación ref {3.7.5} como
[ label {3.7.14} V (x, y) = dfrac {Q} {4 pi epsilon_0} left ( dfrac {1} {r_1} – dfrac {1} {r_2 } right), ]
donde (r_1 ^ 2 = (x-L) ^ 2 + y ^ 2 text {y} r_2 ^ 2 = (x + L) ^ 2 + y ^ 2 ). Si, como antes, expresamos distancias en términos de (L ) y (V ) en unidades de ( dfrac {Q} {4 pi epsilon_0 L} ), la expresión para el potencial se convierte en [ 19459002]
[ label {3.7.15} V (x, y) dfrac {1} {r_1} – dfrac {1} {r_2}, ]
donde (r_1 ^ 2 = (x + 1) ^ 2 + y ^ 2 text {y} r_2 ^ 2 = (x-1) ^ 2 + y ^ 2 ).
Una forma de graficar los equipotenciales sería calcular (L ) para una cuadrícula completa de valores de ((x, y) ) y luego usar una rutina de trazado de contorno para dibujar los equipotenciales. Mis habilidades informáticas no están a la altura, así que voy a ver si podemos encontrar alguna forma de trazar los equipotenciales directamente.
Presento dos métodos. En el primer método, uso la ecuación ref {3.7.15} y trato de manipularla para poder calcular (y ) en función de (x ) y (L ). El segundo método me lo mostró J. Visvanathan de Chennai, India. Haremos ambas cosas y luego las compararemos.
Primer método.
Para anticipar, vamos a necesitar lo siguiente:
[ begin {align} & r_1 ^ 2r_2 ^ 2 = (x ^ 2 + y ^ 2 + 1) ^ 2-4x ^ 2 = B ^ 2-A, label {3.7.16} \ & r_1 ^ 2 + r_2 ^ 2 = 2 (x ^ 2 + y ^ 2 + 1) = 2B, label {3.7.17} \ text {and} quad & r_1 ^ 4 + r_2 ^ 4 = 2 [(x ^ 2 + y ^ 2 + 1) ^ 2 + 4x ^ 2] = 2 (B ^ 2 + A), label {3.7.18} \ text {where} quad , & A = 4x ^ 2 etiqueta {3.7.19} \ text {y} quad & B = x ^ 2 + y ^ 2 + 1 label {3.7.20} \ end {align} ]
Ahora la ecuación ref {3.7.15} es (r_1r_2 V = r_2-r_1 ). Para extraer (y ) es necesario cuadrar esto dos veces, para que (r_1 text {y} r_2 ) aparezca solo como (r_1 ^ 2 text {y} r_2 ^ 2 ). Después de un poco de álgebra, obtenemos
[ label {3.7.21} r_1 ^ 2r_2 ^ 2 [2-V ^ 4r_1 ^ 2r_2 ^ 2 + 2V ^ 2 (r_1 ^ 2 + r_2 ^ 2)] = r_1 ^ 4 + r_2 ^ 4. ]
Al sustituir las ecuaciones ref {3.7.16}, 17,18, para las cuales estamos bien preparados, encontramos para la ecuación a los equipotenciales una ecuación que, después de un poco de álgebra, puede escribirse como una ecuación cuántica en B :
[ begin {align} & a_0 + a_1B + a_2B ^ 2 + a_3B ^ 3 + a_4B ^ 4 = 0 label {3.7.22} \ text {where} quad & a_0 = A (4 + V ^ 4A), label {3.7.23} \ & a_1 = 4V ^ 2A, label {3.7.24} \ & a_2 = -2V ^ 2A, label {3.7.25} \ & a_3 = -4V ^ 2 , label {3.7.26} \ text {y} quad & a_4 = V ^ 4. label {3.7.27} \ end {align} ]
El algoritmo será el siguiente: para un determinado (V ) y (x ), calcule los coeficientes cuárticos de las ecuaciones ref {3.7.23} – ref {3.7.27}. Resuelva la ecuación cuártica ref {3.7.22} para B . Calcule y a partir de la ecuación ref {3.7.20}. Mi intento de hacer esto se muestra en la Figura (III ) .11. Se supone que el dipolo tiene una carga negativa en (−1, 0) y una carga positiva en (+1, 0). Los equipotenciales se extraen para (V ) = 0.05, 0.10, 0.20, 0.40, 0.80.
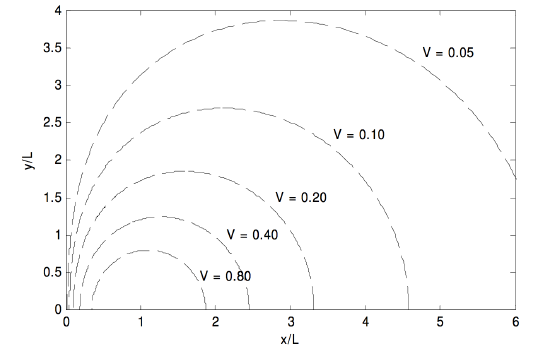
( text {FIGURA III.11} )
Segundo método (J. Visvanathan).
En este método, trabajamos en coordenadas polares, pero en lugar de usar las coordenadas ((r, θ) ), en las que el origen, o polo, del sistema de coordenadas polares está en el centro del dipolo ( ver Figura (III ). 7), utilizamos las coordenadas ((r_1, phi) ) con origen en la carga positiva.
Desde el triángulo, vemos que
[r_2 ^ 2 = r_1 ^ 2 + 4L ^ 2 + 4Lr_1 cos phi. Label {3.7.28} ]
Para referencia futura, observamos que
[ dfrac {∂r_2} {∂r_1} = dfrac {r_1 + 2L cos phi} {r_2}. Label {3.7.29} ]
Siempre que las distancias se expresen en unidades de (L ), estas ecuaciones se convierten en
[ label {3.7.30} r_2 ^ 2 = r_1 ^ 2 + 4r_1 cos phi + 4, ]
[ dfrac {∂r_2} {∂r_1} = dfrac {r_1 + 2 cos phi} {r_2}. Label {3.7.31} ]
Si, además, el potencial eléctrico se expresa en unidades de ( dfrac {Q} {4 pi epsilon_0 L} ), el potencial en P se da, como antes (ecuación ref {3.7.15 }), por
[ label {3.7.32} V (r_1, phi) = dfrac {1} {r_1} – dfrac {1} {r_2}. ]
teniendo en cuenta que (r_2 ) viene dado por la ecuación ref {3.7.31}.
Por diferenciación con respecto a (r_1 ), tenemos
[ label {3.7.34} f ‘(r_1) = – dfrac {1} {r_1 ^ 2} + dfrac {1} {r_2 ^ 2} dfrac {∂r_2} {∂r_1} = – dfrac {1} {r_1 ^ 2} + dfrac {r_1 + 2 cos phi} {r_2 ^ 3}, ]
y estamos listos para comenzar una iteración de Newton-Raphson: (r_1 = r_1-f / f ‘). Después de haber eliminado (r_1 ), podemos obtener las coordenadas ((x, , y) ) de (x = 1 + r_1 cos φ text {y} y = r_1 sin φ ).
Probé este método y obtuve exactamente el mismo resultado que con el primer método y como se muestra en la Figura (III ). 11.
Entonces, ¿qué método preferimos? Bueno, cualquiera que haya trabajado en detalle las derivaciones de las ecuaciones ref {3.7.16} – ref {3.7.27}, y luego haya intentado programarlas para una computadora, aceptará que el primer método es muy laborioso y incómodo. En comparación, el método de Visvanathan es mucho más fácil de derivar y programar. Por otro lado, un pequeño punto a favor del primer método es que no involucra funciones trigonométricas, por lo que el cálculo numérico es potencialmente más rápido que el segundo método en el que se calcula una función trigonométrica en cada iteración del proceso Newton-Raphson . Sin embargo, en verdad, una computadora moderna realizará el cálculo por cualquiera de los métodos aparentemente instantáneamente, de modo que una pequeña ventaja no es relevante.
Hasta ahora, hemos logrado acercar los equipotenciales cerca del dipolo. Las líneas de fuerza son ortogonales a los equipotenciales. Después de probar varios métodos con solo un éxito parcial, estoy agradecido al Dr. Visvanathan, quien me señaló cuál debería haber sido el método “obvio”, es decir, usar la ecuación ref {3.7.12}, que, en nuestro ( (r_1, phi) ) sistema de coordenadas basado en la carga positiva, es (r_1 dfrac {d phi} {dr_1} = dfrac {E_ phi} {E_ {r_1}} ), tal como nosotros hizo por la gran distancia, dipolo pequeño, aproximación. En este caso, el potencial viene dado por las ecuaciones ref {3.7.30} y ref {3.7.32}. (Recuerde que en estas ecuaciones, las distancias se expresan en unidades de L y el potencial en unidades de ( dfrac {Q} {4 pi epsilon_0 L} ).) Los componentes radial y transversal del campo están dados por (E_ {r_1} = – dfrac {∂V} {∂ {r_1}} text {y} E_ phi = – dfrac {1} {r_1} dfrac {∂V} {∂ phi} ), que da como resultado
[E_ {r_1} = dfrac {1} {r_1 ^ 2} – dfrac {r_1 + 2 cos phi} {r_2 ^ 3} label {3.7.35} ]
y
[E_ phi = dfrac {2 sin phi} {r_2 ^ 3}. Label {3.7.36} ]
Aquí, el campo se expresa en unidades de ( dfrac {Q} {4 pi epsilon_0L ^ 2} ), aunque eso apenas importa, ya que solo nos interesa la relación. Al aplicar (r_1 dfrac {d phi} {dr} = dfrac {E_ phi} {E_ {r_1}} ) a estos componentes de campo obtenemos la siguiente ecuación diferencial a las líneas de fuerza:
[d phi = dfrac {2r_1 sin phi} {(r_1 ^ 2 + 4 + 4r_1 cos phi) ^ {3/2} -r_1 ^ 2 (r_1 + 2 cos phi )} dr_1. label {3.7.37} ]
Por lo tanto, se puede comenzar con algunos (φ_0 ) y pequeños (r_2 ) y aumentar (r_1 ) sucesivamente en pequeños incrementos, calculando un nuevo φ cada vez. Los resultados se muestran en la Figura (III ). 12, en la que los equipotenciales se dibujan para los mismos valores que en la Figura (III ). 11, y los ángulos iniciales para las líneas de fuerza son 30º, 60º, 90º 120º, 150º.
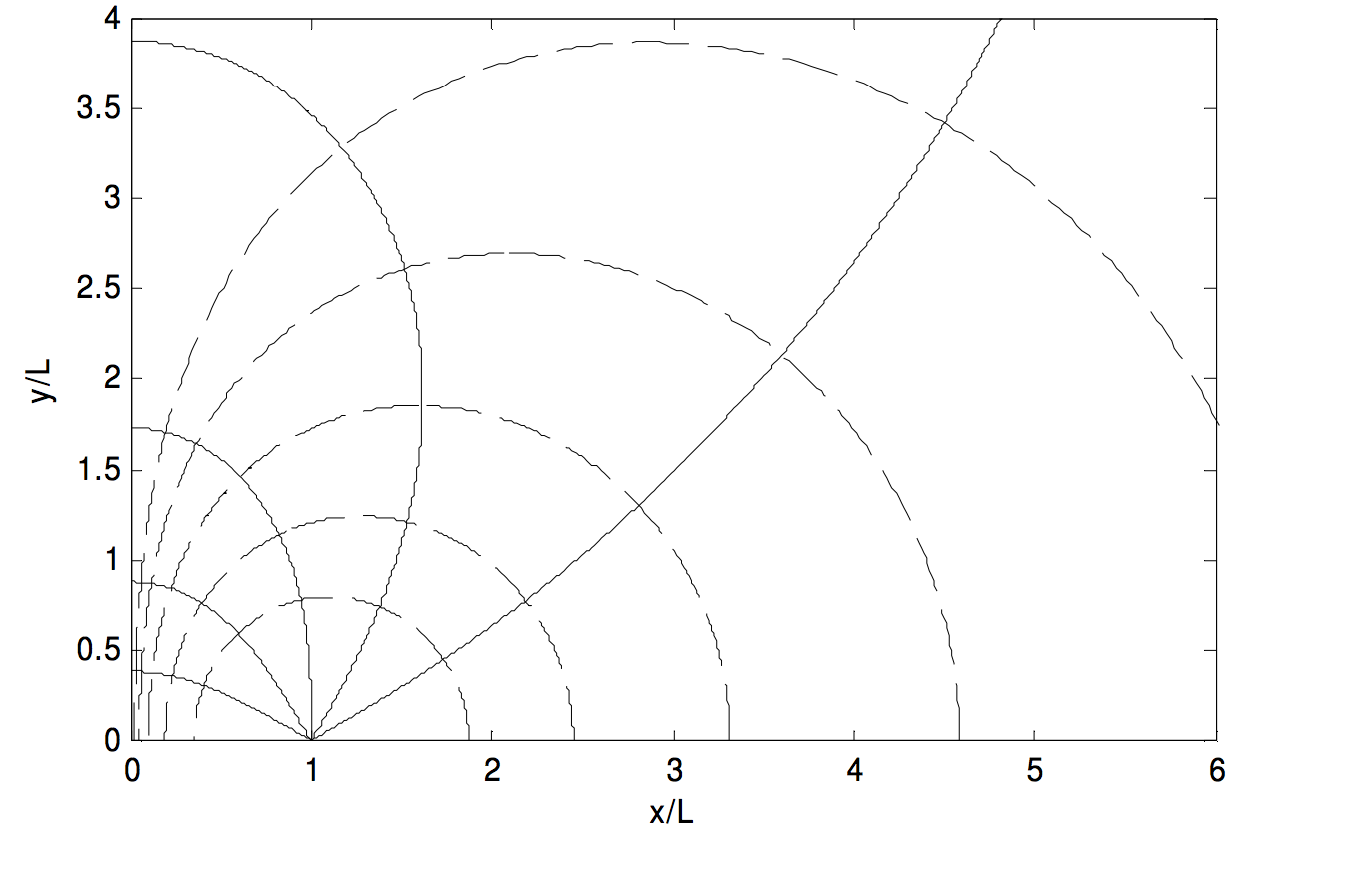
( text {FIGURA III.12} )
Antes de abandonar esta sección, aquí hay otro método para calcular el potencial cercano a un dipolo, para aquellos que están familiarizados con los polinomios de Legendre.
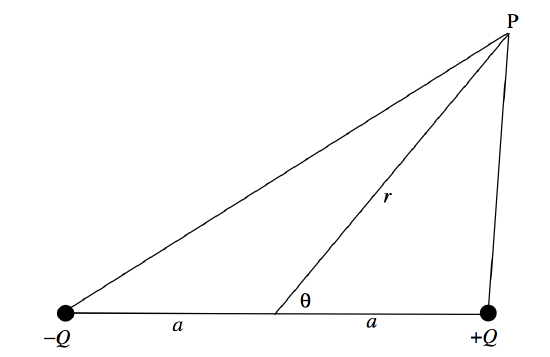
El potencial en P viene dado por
[ nonumber begin {align} 4 pi epsilon_0V & = Q left [ dfrac {1} {(a ^ 2 + r ^ 2-2ar cos theta) ^ {1/2}} – dfrac {1} {(a ^ 2 + r ^ 2 + 2ar cos theta) ^ {1/2}} right] \ nonumber & = dfrac {Q} {a} left [ dfrac {1} {(1-2 rho cos theta + rho ^ 2) ^ {1/2}} – dfrac {1} {1 + 2 rho cos theta + rho ^ 2) ^ {1/2}} right] \ end {align} ]
donde ( rho = r / a ).
Es bien sabido (para aquellos que están familiarizados con los polinomios de Legendre) que
[ nonumber (1-2 rho cos theta + rho ^ 2) ^ {- 1/2} = P_0 ( cos theta) + P_1 ( cos theta) rho + P_2 ( cos theta) rho ^ 2 + P_3 (x) rho ^ 3 + … ]
donde (P_n ) son los polinomios de Legendre. Por lo tanto, el potencial puede calcularse como una expansión en serie. Aquellos que no estén familiarizados con los polinomios de Legendre pueden encontrar algo sobre ellos en mis notas sobre mecánica celeste www.astro.uvic.ca/~tatum/celmechs/celm1.pdf