Deseamos encontrar el potencial en un punto P a una gran distancia (R ) de un cuerpo cargado, en términos de su carga total y sus momentos dipolo, cuadrupolo y posiblemente de orden superior. No habrá pérdida de generalidad si elegimos un conjunto de ejes tal que P esté en el eje (z ).
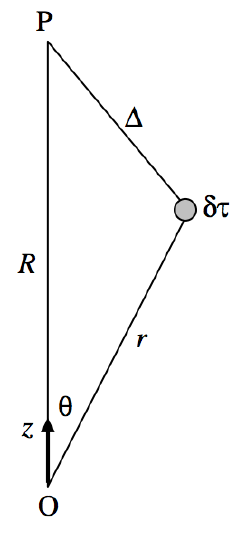
( text {FIGURE III.14} )
Nos referimos a la Figura (III ). 14, y consideramos un elemento de volumen ( δτ ) a una distancia r de algún origen. El punto P está a una distancia r del origen y una distancia (∆ text {from} δτ ). El potencial en P de la carga en el elemento (δτ ) viene dado por
[4 pi epsilon_0 delta V = dfrac { rho delta tau} { Delta} = dfrac { rho} {R} left (1+ dfrac {r ^ 2} {R ^ 2} – dfrac {2r} {R} cos theta right) ^ {- 1/2} delta tau, ]
y así el potencial de la carga en todo el cuerpo está dado por
[4 pi epsilon_0 V = dfrac {1} {R} int rho left (1+ dfrac {r ^ 2} {R ^ 2} – dfrac {2r} {R} cos theta right) ^ {- 1/2} delta tau. ]
Al expandir los paréntesis por el teorema binomial, encontramos, después de un pequeño problema, que esto se convierte en
[4 pi epsilon_0 V = dfrac {1} {R} int rho , d tau + dfrac {1} {R ^ 2} int rho r P_1 ( cos theta) , d tau + dfrac {1} {2! R ^ 3} int rho r ^ 2 P_2 ( cos theta)] , d tau + dfrac {1} {3! R ^ 4} int rho r ^ 3 P_3 ( cos theta) , d tau + …, ]
donde los polinomios P son los polinomios Legendre dados por [19459 002]
[ begin {align} P_1 ( cos theta) & = cos theta \ P_2 ( cos theta) & = dfrac {1} {2} (3 cos ^ 2 theta -1), \ P_3 ( cos theta) & = dfrac {1} {2} (5 cos ^ 3 theta – 3 cos theta). \ end {align} ]
Vemos por las formas de estas integrales y las definiciones de los componentes de los momentos dipolo y cuadrupolo que ahora se puede escribir:
[ 4 pi epsilon_0 V = dfrac {Q} {R} + dfrac {p} {R ^ 2} + dfrac {1} {2R ^ 3} (3q_ {zz} -Tr textbf {q}) + …, label {3.9.7} ]
Aquí Tr q es el rastro de la matriz de momento cuadrupolo, o la suma (invariante) de sus elementos diagonales. La ecuación ref {3.9.7} también se puede escribir
[4 pi epsilon_0V = dfrac {Q} {R} + dfrac {p} {R ^ 2} + dfrac {1 } {2R ^ 3} [2q_ {zz} – (q_ {xx} + q_ {aa})] + …. ]
La cantidad (2q_ {zz} – (q_ {xx} + q_ {aa}) ) de la matriz diagonalizada a menudo se conoce como “el” momento cuadrupolo. Es cero si los tres componentes diagonales son cero o si (q_ {zz} = dfrac {1} {2} (q_ {xx} + q_ {aa}) ). Si el cuerpo tiene simetría cilíndrica sobre el eje (z ), esto se convierte en (2 (q_ {zz} -q_ {xx}) ).
Ejercicio
Muestre que el potencial en ((r, θ) ) a una gran distancia del cuadrupolo lineal de la Figura (III ). 15 es
[ V = dfrac {QL ^ 2 (3 cos ^ 2 theta -1)} {4 pi epsilon_0 r ^ 3}. Nonumber ]
(El espacio en la línea discontinua está previsto para indicar que r es muy grande en comparación con L .)
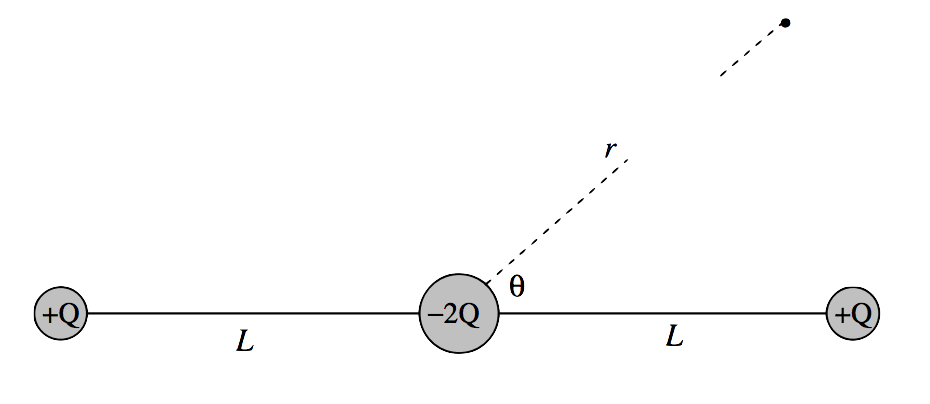
( text {FIGURA III.15} ) [19459002 ]
La solución a este ejercicio es fácil si conoce acerca de Polinomios Legendre . Ver la Sección 1.14 de mis notas sobre Mecánica Celestial. Lo que necesita saber es que la expansión de ((1-2ax + x ^ 2) ^ {- 1/2} ) se puede escribir como una serie de polinomios de Legendre, a saber, (P_0 (x) + xP_1 ( x) + x ^ 2P_2 (x) + … ). También necesita una tabla (muy pequeña) de polinámicos Legendre, a saber, (P_0 (x) = 1, , P_1 (x) = x, , P_2 (x) = dfrac {1} {2} (3x ^ 2-1) ). Teniendo en cuenta eso, el ejercicio debería resultarle muy fácil.