El momento magnético y el momento angular son propiedades importantes de las partículas subatómicas. Sin embargo, cada uno de ellos depende de la velocidad angular de rotación de la partícula. La relación de momento magnético a momento angular, por otro lado, es independiente de la velocidad de rotación, y nos dice algo sobre cómo se distribuyen la masa y la carga dentro de la partícula. Además, se puede medir con mayor precisión que el momento magnético o el momento angular por separado. Esta relación se denomina relación magnetogírica (o, perversa e ilógicamente, por algunos, la “relación giromagnética”). Debería poder demostrar que las dimensiones de la relación magnetogírica son ( text {QM} ^ {- 1} ) y, por lo tanto, la unidad SI es ( text {C kg} ^ {- 1} ) . Sin embargo, dudo que muchos físicos de partículas usen unidades tan simples. Probablemente expresan el momento magnético en magnetons de Bohr o magnetons nucleares y el momento angular en unidades de constante de Planck dividido por (2 pi ), pero ese no es nuestro problema.
Calculemos la relación magnetogírica de una carga puntual y una masa puntual que se mueve en una órbita circular, como el electrón que se mueve alrededor del protón en el modelo más simple de un átomo de hidrógeno. Supondremos que la velocidad angular en la órbita es ( omega ) y el radio de la órbita es (a ). El momento angular es fácil: es solo (ma ^ 2 omega ). La frecuencia con la que la partícula (cuya carga es (Q )) pasa un punto dado en su órbita es ( omega / (2 pi) ), por lo que la corriente es (Q omega / (2 Pi)). El área de la órbita es ( pi a ^ 2 ) y, por lo tanto, el momento magnético de la partícula en órbita es ( frac {1} {2} Q omega a ^ 2 ). La relación magnetogírica es, por lo tanto, (Q / (2m) ).
La relación magnetogírica será la misma en cualquier cuerpo giratorio en el que las distribuciones de densidad de masa y densidad de carga dentro del cuerpo sean las mismas. Considere, sin embargo, la relación magnetogírica de una esfera de metal giratoria cargada. La masa se distribuye uniformemente en toda la esfera, pero toda la carga reside en la superficie. Entonces podemos esperar que la relación magnetogírica sea bastante mayor que (Q / (2m) ).
El momento angular es fácil. Es solo ( frac {2} {5} ma ^ 2 omega ). Ahora para el momento magnético. Consulte la Figura ( text {VII.6} ).
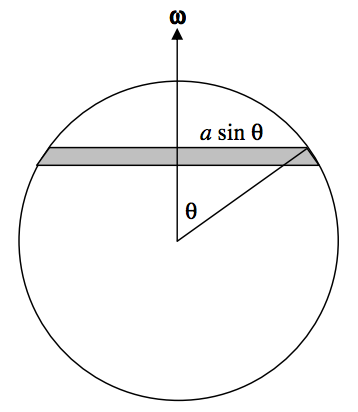
( text {FIGURE VII.6} )
El área de la zona elemental que se muestra es (2 pi a ^ 2 sin theta d theta ). El área de toda la esfera es (4 pi a ^ 2 ), por lo que la carga en la zona elemental es ( frac {1} {2} Q sin theta d theta ). La zona gira, al igual que toda la esfera, a una velocidad angular ( omega ), por lo que la corriente es
[ frac {1} {2} Q sin theta d theta times omega / (2 pi) = frac {Q omega sin theta d theta} {4 pi} ]
El área encerrada por el elemental zona es ( pi a ^ 2 sin ^ 2 theta ). El momento magnético (dp_m ) de la zona es el tiempo actual del área encerrada, que es
[dp_m = frac {1} {4} Q omega a ^ 2 sin ^ 3 theta d theta ]
El momento magnético de toda la esfera se encuentra integrando esto desde ( theta ) = 0 a ( pi ), de donde
[ p_m = frac {1} {3} Q omega a ^ 2 ]
La relación del momento magnético al momento angular es, por lo tanto, (5Q / (6m) ).
Aquellos que estén familiarizados con el movimiento giroscópico sabrán que si un cuerpo giratorio de momento angular ( textbf {L} ) está sujeto a un torque ( tau ) , el vector de momento angular no será constante en la dirección y, de hecho, la tasa de cambio de momento angular será igual a ( tau ) . La figura ( text {VII.7} ) es un recordatorio del movimiento de una parte superior en precesión regular (es decir, sin nutación).
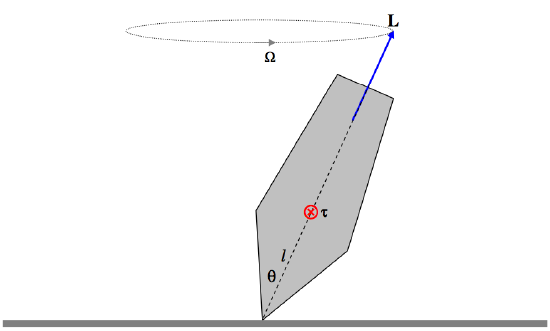
( text {FIGURE VII.7} )
Se necesitará un estudio del Capítulo 4 Sección 4.10 de Mecánica clásica para una comprensión más detallada de la movimiento de un top. La parte superior está sujeta a un par de magnitud (mgl sin theta ). El par puede ser representado por un vector ( tau ) dirigido al plano del papel. Como se dibuja, el vector de momento angular ( textbf {L} ) forma un ángulo ( theta ) con el campo gravitacional ( textbf {g} ), y precesa sobre la vertical con una velocidad angular [ 19459009] ( Omega ) , los tres vectores ( tau ) , ( textbf {L} ) y ( Omega ) estar relacionado por ( tau = textbf {L} times Omega ) . La magnitud del vector de momento angular es, por lo tanto, ( tau / (L sin theta) ). Pero ( tau = mgl sin theta ), de modo que la frecuencia de precesión es (mgl / L ), independiente de ( theta ). Del mismo modo, un cuerpo giratorio cargado con un momento magnético de ( textbf {p} _m ) es un campo magnético ( textbf {B} ) experimenta un par ( tau = textbf {p} _m times textbf {B} ) , que es de magnitud (p_mB sin theta ), y en consecuencia su vector de momento angular precesa alrededor de ( textbf {B} ) a una velocidad angular ( frac {p_m} {L} B ), independiente de ( theta ). (Verifique que esto tenga dimensiones ( text {T} ^ {- 1} ).) El coeficiente de (B ) aquí es la relación magnetogírica. La velocidad de precesión se puede medir con mucha precisión y, por lo tanto, la relación magnetogírica se puede medir de manera correspondiente con precisión. Este fenómeno de “precesión de Larmor” es la base de muchos instrumentos y disciplinas interesantes, como el magnetómetro de precesión de protones, la espectroscopía de resonancia magnética nuclear y las imágenes de resonancia magnética nuclear utilizadas en medicina. Debido a que cualquier cosa que incluya la palabra “nuclear” es una frase políticamente incorrecta, la palabra “nuclear” generalmente se descarta, y la resonancia magnética nuclear generalmente se llama simplemente “resonancia magnética”, o MRI, que no tiene mucho sentido, pero al menos es políticamente correcto.