Ya sabemos que una corriente eléctrica ( textbf {I} ) que fluye en una región del espacio donde existe un campo magnético ( textbf {B} ) experimentará una fuerza en ángulo recto para tanto ( textbf {I} ) como ( textbf {B} ), y la fuerza por unidad de longitud, ( textbf {F} ^ prime ), viene dada por
[ textbf {F} ^ prime = textbf {I} times textbf {B} label {8.3.1} ]
y de hecho utilizamos esta ecuación para definir lo que queremos decir con ( textbf {B} ). La ecuación ref {8.3.1} se ilustra en la Figura ( text {VIII.1} ).
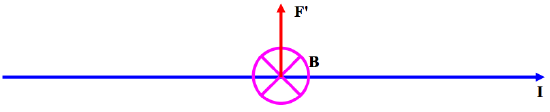
( text {FIGURE VIII.1} )
La cruz grande en un círculo tiene la intención de indicar un campo magnético dirigido al plano del papel , y ( textbf {I} ) y ( textbf {F} ^ prime ) muestran las direcciones de la corriente y la fuerza.
Ahora podríamos considerar que la corriente comprende una corriente de partículas, (n ) de ellas por unidad de longitud, cada una con una carga (q ), y moviéndose con velocidad ( textbf {v } ) (velocidad (v )). La corriente es entonces (nq textbf {v} ), y la ecuación ref {8.3.1} muestra que la fuerza sobre cada partícula es
[ textbf {F} = q textbf {v} times textbf {B}. label {8.3.2} ]
Esta, entonces, es la ecuación que da la fuerza sobre una partícula cargada que se mueve en un campo magnético, y la fuerza se conoce como la fuerza de Lorentz .
Se notará que hay una fuerza sobre una partícula cargada en un campo magnético solo si la partícula se mueve , y la fuerza está en ángulo recto con ambos ( textbf { v} ) y ( textbf {B} ).
En cuanto a la pregunta: “¿Quién puede decir si la partícula se mueve?” o “moviéndose en relación con qué?” Eso nos lleva a aguas muy profundas. Para una respuesta, lo remito al siguiente artículo: Einstein, A., Zur Elektrodynamik Bewegter Körper, Annalen der Physik 17 , 891 (1905) .
Supongamos que tenemos una partícula, de carga (q ) y masa (m ), que se mueve con velocidad (v ) en el plano del papel, y que hay un campo magnético ( textbf {B} ) dirigido en ángulo recto al plano del papel. (¡Si está leyendo esto directamente de la pantalla, lea “plano de la pantalla”!) La partícula experimentará una fuerza de magnitud (qv ) (B ) (porque ( textbf {v} ) y ( textbf {B} ) están en ángulo recto entre sí), y esta fuerza está en ángulo recto con la velocidad instantánea de la partícula. Debido a que la fuerza está en ángulo recto con el vector de velocidad instantánea, la velocidad de la partícula no se ve afectada. Su aceleración es de magnitud constante y, por lo tanto, la partícula se mueve en un círculo , cuyo radio se determina igualando la fuerza (qv ) (B ) con la masa multiplicada por la aceleración centrípeta. Eso es (qv ) (B = mv ^ 2 / r ), o
[r = dfrac {mv} {qB} label {8.3.3} ]
Si observamos el movimiento de alguna partícula subatómica en un campo magnético, y tenemos razones para creer que la carga es igual a la carga electrónica (o quizás un pequeño múltiplo de ella), vemos que el radio de el camino circular nos dice el momento de la partícula; es decir, el producto de su masa y velocidad. La ecuación ref {8.3.3} es bastante válida para velocidades relativistas, excepto que la masa que aparece en la ecuación es entonces la masa relativista, no la masa en reposo, de modo que el radio es una función ligeramente más complicada de la velocidad y la masa en reposo .
Si ( textbf {v} ) y ( textbf {B} ) no son perpendiculares entre sí, podemos resolver ( textbf {v} ) en un componente ( v_1 ) perpendicular a ( textbf {B} ) y un componente (v_2 ) paralelo a ( textbf {B} ). La partícula se moverá entonces en una trayectoria helicoidal , siendo el radio de la hélice (mv_2 / (qB) ), y el centro del círculo moviéndose a la velocidad (v_2 ) en la dirección de ( textbf {B} ).
La velocidad angular ( omega ) de la partícula en su trayectoria circular es ( omega = v / r ), que, en concierto con la ecuación ref {8.3.3}, da [ 19459002]
[ omega = dfrac {qB} {m}. Label {8.3.4} ]
Esto se llama la velocidad angular del ciclotrón o la [ 19459005] frecuencia angular del ciclotrón . Debe verificar que sus dimensiones sean ( text {T} ^ {- 1} ).
Un magnetrón es un tubo de vidrio cilíndrico evacuado con dos electrodos en su interior. Uno, el electrodo negativo (cátodo) es un cable a lo largo del eje del cilindro. Está rodeado por un ánodo cilíndrico hueco de radio (a ). Un campo magnético uniforme se dirige paralelo al eje del cilindro. El cátodo se calienta (y emite electrones, de carga (e ) y masa (m )) y se establece una diferencia de potencial (V ) a través de los electrodos. Por consiguiente, los electrones alcanzan una velocidad dada por
[eV = dfrac {1} {2} mv ^ 2. Label {8.3.5} ]
Debido al campo magnético , se mueven en arcos de círculos. A medida que aumenta el campo magnético, el radio de los círculos se vuelve más pequeño y, cuando el diámetro del círculo es igual al radio (a ) del ánodo, no hay electrones que puedan alcanzar el ánodo y la corriente a través del magnetrón. De repente cae. Esto sucede cuando
[ dfrac {1} {2} a = dfrac {mv} {eB}. Label {8.3.6} ]
Eliminación de (v ) de las ecuaciones ref {8.3.5} y ref {8.3.6} muestra que la corriente cae a cero cuando
[B = sqrt { dfrac {8mV} {ea ^ 2} }. label {8.3.7} ]
Los expertos en relatividad especial deberían intentarlo con las fórmulas relativistas. En la ecuación ref {8.3.5} el lado derecho tendrá que ser (( gamma-1) m_0c ^ 2 ), y en la ecuación ref {8.3.6} (m ) tendrá que ser reemplazado con ( gamma m_0 ). Hago el resultado
[B = dfrac {2 sqrt {2m_0c ^ 2eV + e ^ 2V ^ 2}} {eac}. Label {8.3.8} ]
[19459001 ] Para pequeñas diferencias de potencial, (eV ) es mucho menor que (m_0c ^ 2 ), y la ecuación ref {8.3.8} se reduce a la ecuación ref {8.3.5}.