La fuerza sobre una partícula cargada en un campo eléctrico y magnético es
[ textbf {F} = q ( textbf {E} + textbf {v} times textbf {B }) ].
Como ejemplo, investiguemos el movimiento de una partícula cargada en campos eléctricos y magnéticos uniformes que están en ángulo recto entre sí. Específicamente, escojamos ejes para que el campo magnético ( textbf {B} ) se dirija a lo largo del eje positivo (z ) y el campo eléctrico se dirija a lo largo del eje positivo (y ). (¡Dibuje esto en un diagrama grande!) Intente e imagine cómo sería el movimiento. Supongamos, por ejemplo, que el movimiento está todo en el plano (yz ). Quizás la partícula se moverá una y otra vez en un círculo alrededor de un eje paralelo al campo magnético, pero el centro de este círculo se acelerará en la dirección del campo eléctrico. Bueno, tienes razón en que la partícula se mueve en un círculo alrededor de un eje paralelo a ( textbf {B} ), y también en que el centro del círculo se mueve. Pero el resto no está del todo bien. Antes de embarcarse en un análisis matemático, vea si puede imaginar el movimiento con un poco más de precisión.
Supondremos que en algún momento los componentes (x ), (y ) y (z ) de la velocidad de la partícula son (u ), (v ) y W). Supondremos que estos componentes de velocidad son todos no relativistas, lo que significa que m es constante y no una función de la velocidad. Los tres componentes de la ecuación de movimiento (ecuación 8.4.1) son entonces
[m dot u = qBv, ]
[m dot v = -qBu + qE ]
y [m dot w = 0. ]
Para abreviar, escribiré (q B / m = omega ) (la velocidad angular del ciclotrón) y, notando que las dimensiones de (E / B ) son las dimensiones de la velocidad (¡verifique esto!), escribiré (E / B = V_D ), donde la importancia del subíndice (D ) hacerse evidente a su debido tiempo. Las ecuaciones de movimiento se convierten en
[ ddot x = dot u = omega v, ]
[ ddot y = dot v = – omega (u- V_D) ]
y [ ddot z = dot w = 0. ]
Para encontrar las soluciones generales a estos, podemos, por ejemplo, dejar (X = u – V_D ). Entonces las ecuaciones 8.4.5 y 8.4.6 se convierten en ( dot X = omega v ) y ( dot v = – omega X ). De estos, obtenemos ( ddot X = – omega ^ 2 X ). La solución general de esto es (X = A sin ( omega t + alpha) ), y entonces (u = A sin ( omega t + alpha) + V_D ). Por integración y diferenciación con respecto al tiempo podemos encontrar (x ) y ( ddot x ) respectivamente. Así obtenemos:
[x = – frac {A} { omega} cos ( omega t + alpha) + V_Dt + D, ]
[u = dot x = A sin ( omega t + alpha) + V_D ]
y [ ddot x = A omega cos ( omega t + alpha). ] [ 19459002]
De manera similar, podemos resolver para y y z de la siguiente manera:
[y = frac {A} { omega} sin ( omega t + alpha) + F, ]
[v = dot y = A cos ( omega t + alpha), ]
[ ddot y = -A omega sin ( omega t + alpha), ]
[z = w_0t + z_0, ]
[w = dot z = w_0 ]
y [ ddot z = 0. ]
Hay seis constantes arbitrarias de integración, a saber, (A ), (D ), (F ), ( alpha ), (z_0 ) y (w_0 ), cuyos valores dependen de las condiciones iniciales (posición y velocidad en (t = 0 )). De estos, (z_0 ) y (w_0 ) son solo los valores iniciales de (z ) y (w ). Supongamos que estos son ambos cero y que todo el movimiento tiene lugar en el plano (xy ).
En estas ecuaciones (A ) y ( alpha ) siempre ocurren en las combinaciones (A sin alpha ) y (A cos alpha ), y por lo tanto por conveniencia Voy a dejar (A sin alpha = S ) y (A cos alpha = C ), y voy a volver a escribir las ecuaciones 8.4.8, 8.4.9, 8.4.11 y 8.4.12 como
[x = – frac {1} { omega} (C cos omega t – S sin omega t) + V_Dt + D, ]
[ 19459001] [u = C sin omega t + S cos omega t + V_D, ]
[y = frac {1} { omega} (C sin omega t + S cos omega t) + F, ]
y [v = C cos omega t – S sin omega t. ]
Supongamos que Las condiciones iniciales son: at (t = 0 ), (x = y = u = v = 0 ). Es decir, la partícula comienza desde el reposo en el origen. Si pone estas condiciones iniciales en las ecuaciones 8.4.17-20, encontramos que (C = 0 ), (S = −V_D ), (D = 0 ) y (F = V_D / omega ). Las ecuaciones 8.4.17 y 8.4.19, que dan la ecuación a la ruta descrita por la partícula, se convierten en
[x = – frac {V_D} { omega} sin omega t + V_D t ]
y [y = frac {V_D} { omega} (1- cos omega t). ]
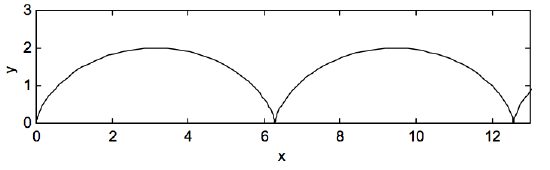
Vale la pena recordarnos aquí que el ciclotrón angular la velocidad es ( omega = qB / m ) y esa (V_D = E / B ), y por lo tanto ( frac {V_D} { omega} = frac {mE} {qB ^ 2} ) . Estas ecuaciones son las ecuaciones paramétricas de un cicloide . (Para más información sobre el cicloide, consulte el Capítulo 19 de las notas de Mecánica clásica de esta serie). El movimiento es un movimiento circular en el que el centro del círculo se desplaza (de ahí el subíndice (D )) en la dirección (x ) – a velocidad (V_D ). La ruta se muestra en la Figura ( text {VIII.2} ), dibujada para distancias en unidades de ( frac {V_D} { omega} = frac {mE} {qB ^ 2} ).
( text {FIGURE VII.2} )
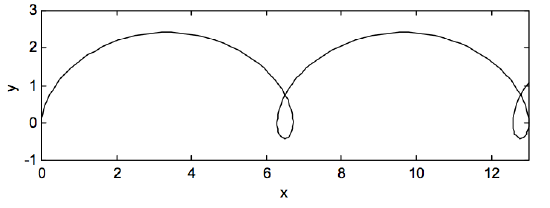
Le dejo al lector que pruebe diferentes condiciones iniciales, como una de (u ) o (v ) no inicialmente cero. Puede intentar con (u_0 ) o (v_0 ) igual a algún múltiplo de fracción de (V_D ), y puede hacer que (u_0 ) o (v_0 ) sea positivo o negativo. Calcule los valores de las constantes (D ), (F ), (C ) y (S ) y dibuje la ruta resultante. Siempre obtendrás algún tipo de cicloide. Puede que no sea un cicloide simple como en nuestro ejemplo, pero podría ser un cicloide expandido (es decir, bucles pequeños en lugar de cúspides) o un cicloide contraído , que no tiene bucles ni cúspides , pero se ve más o menos sinusoidal. Probaré solo uno. Dejaré (u_0 = 0 ) y (v_0 = + V_D ). Si hago eso, obtengo
[x = frac {V_D} { omega} (1- cos omega t – sin omega t) + V_Dt ]
[19459001 ] y [y = frac {V_D} { omega} (1- cos omega t + sin omega t). ]
Esto se ve así:
( text {FIGURA VII.3} )