Doy esto como un ejemplo bastante más difícil, no apto para principiantes, solo para ilustrar cómo se puede calcular el movimiento de una partícula cargada en un campo magnético que no es uniforme. Supongo que tenemos una corriente eléctrica (I ) que fluye (en un cable) en la dirección positiva (z ) hacia arriba en el eje (z ). Un electrón de masa (m ) y una carga de magnitud (e ) (es decir, su carga es (- e )) está deambulando cerca de la corriente. La corriente produce un campo magnético y, en consecuencia, el electrón, cuando se mueve, experimenta una fuerza de Lorenz. En la siguiente tabla escribo, en coordenadas cilíndricas, los componentes del campo magnético producido por la corriente, los componentes de la fuerza de Lorentz sobre el electrón y las expresiones en coordenadas cilíndricas para el componente de aceleración. Se necesitará cierta facilidad en mecánica clásica para seguir esto.
begin {array} {c | lcr} & text {Field} & text {Force} & text {Acceleration} \ hline rho & B_ rho = 0 & e dot z B_ phi & ddot rho – rho dot phi ^ 2 \ phi & B_ phi = frac { mu_0I} {2 pi rho} & 0 & rho ddot phi + 2 dot rho dot phi \ z & B_z = 0 & -e dot rho B_ phi & ddot z \ nonumber end {array}
Desde esta tabla podemos escriba las ecuaciones de movimiento , de la siguiente manera, en la que (S_C ) es la abreviatura de ( frac { mu_0eI} {2 pi m} ). Esta cantidad tiene las dimensiones de velocidad (¡verificar!) Y voy a llamarla velocidad característica . Tiene el valor numérico (3.5176 times 10 ^ 4 text {I m s} ^ {- 1} ), donde (I ) está en (A ). Las ecuaciones de movimiento, entonces, son
Radial: [ rho ( ddot rho – rho dot phi ^ 2) = S_C dot z ]
Transverso ( Azimutal): [ rho ddot phi + 2 dot rho dot phi = 0 ]
Longitudinal: [ rho ddot z = -S_C dot rho. ]
Será conveniente definir componentes de velocidad adimensional:
[u = dot rho / S_C, qquad v = rho dot phi / S_C, qquad w = dot z / S_c. label {8.5.4a, b, c} ]
Suponga que inicialmente, en el tiempo (t = 0 ), sus valores son (u_0 ), ( v_0 ) y (w_0 ), y también que la distancia inicial de la partícula desde la corriente es ( rho_0 ). Además, introduzca la distancia adimensional
[x = rho / rho_0, ]
para que el valor inicial de (x ) sea 1. Los valores iniciales de ( phi ) y (z ) pueden tomarse como cero mediante la elección adecuada de ejes.
La integración de las ecuaciones 8.5.2 y 3, con estas condiciones iniciales, produce
[ dot z = S_C (w_0 – ln ( rho / rho_0)) ] [ 19459002]
y [ rho ^ 2 dot phi = rho_0 v_0 S_C; ]
o, en términos de variables adimensionales,
[w = w_0 – ln x ]
y [v = v_0 / x. ]
Podemos escribir ( dot rho frac {d dot rho} {d rho} ) para ( ddot rho ) en la ecuación 8.5.1, y la sustitución de ( dot z ) y ( dot phi ) de las ecuaciones 8.5.6 y 8.5.7 arroja [19459002 ]
[u ^ 2 = u_0 ^ 2 + v_0 ^ 2 (1-1 / x ^ 2) + 2 w_0 ln x – ( ln x) ^ 2. ]
Ecuaciones 8.5.8,9 y 10 dan los componentes de velocidad del electrón en función de su distancia desde el cable.
La ecuación 8.5.2 expresa el hecho de que no hay fuerza transversal (azimutal). Su integral de tiempo, la ecuación 8.5.7) expresa la consecuencia de que el componente (z ) de su momento angular se conserva. Además, de las ecuaciones 8.5.8,9 y 10, encontramos que
[u ^ 2 + v ^ 2 + w ^ 2 = u_0 ^ 2 + v_0 ^ 2 + w_0 ^ 2 = s ^ 2 , text {say}, ]
para que la velocidad del electrón sea constante. Esto es como se esperaba, ya que la fuerza sobre el electrón siempre es perpendicular a su velocidad; el punto de aplicación de la fuerza no se mueve en la dirección de la fuerza, que por lo tanto no funciona, por lo que se conserva la energía cinética y, por lo tanto, la velocidad.
La distancia del electrón al cable está limitada por debajo y por encima. Los límites inferior y superior, (x_1 ) y (x_2 ) se encuentran en la ecuación 8.5.10 poniendo (u = 0 ) y resolviendo (x ). En la Tabla ( text {VIII.I} ) se muestran ejemplos de estos límites para una variedad de condiciones iniciales.
( text {TABLA VII.1} )
( text {LÍMITES DEL MOVIMIENTO} )
begin {array} {c qquad c qquad l qquad c qquad r} | u_0 | & | v_0 | & | w_0 | & x_1 & x_2 \ 0 & 0 & −2 & 0.018 & 1.000 \ 0 & 0 & −1 & 0.135 & 1.000 \ 0 & 0 & 0 & 1.000 & 1.000 \
0 & 0 & 1 & 1.000 y 7.389 \
0 y 0 y 2 y 1.000 y 54.598 \
0 y 1 y −2 y 0.599 y 1.000 \
0 y 1 y −1 y 1.000 y 1.000 \ [ 19459005] 0 y 1 y 0 y 1.000 y 2.501 \
0 y 1 y 1 y 1.000 y 11.149 \
0 y 1 y 2 y 1.000 y 69.132 \
0 y 2 y −2 & 1.000 y 1.845 \
0 y 2 y −1 y 1.000 y 3.137 \
0 y 2 y 0 y 1.000 y 7.249 \
0 y 2 y 1 y 1.000 y 25.398 \ [ 19459005] 0 y 2 y 2 y 1.000 y 125.009 \
1 y 0 y −2 y 0.014 y 1.266 \
1 y 0 y −1 y 0.089 y 1.513 \
1 y 0 y 0 y 0.368 y 2.718 \
1 y 0 y 1 y 0.661 y 11.181 \
1 y 0 y 2 y 0.790 y 69.135 \
1 y 1 y −2 y 0.476 y 1.412 \
1 y 1 y −1 y 0.602 y 1.919 \
1 y 1 y 0 y 0.726 y 4.024 \
1 y 1 y 1 y 0.809 y 15.345 \
1 y 1 y 2 y 0.857 y 85.581 \
1 y 2 y −2 y 0.840 y 2.420 \
1 y 2 y −1 y 0.873 y 4.052 \
1 y 2 y 0 y 0.896 y 9.259
1 y 2 y 1 y 0.912 y 31.458 \
1 y 2 y 2 y 0.925 y 148.409 \
2 y 0 y −2 y 0.008 y 2.290 \
2 y 0 & −1 y 0.039 y 3.442 \
2 y 0 y 0 y 0.135 y 7.389 \
2 y 0 y 1 y 0.291 y 25.433 \
2 y 0 y 2 y 0.437 y 125.014
2 y 1 y −2 y 0.352 y 2.654 \
2 y 1 y −1 y 0.409 y 4.212 \
2 y 1 y 0 y 0.474 y 9.332 \
2 y 1 y 1 y 0.542 y 31.478 \
2 y 1 y 2 y 0.605 y 148.412 \
2 y 2 y −2 y 0.647 y 4.183 \
2 y 2 y −1 y 0.681 y 7.297 \
2 y 2 y 0 y 0.712 y 16.877 \
2 y 2 y 1 y 0.740 y 54.486 \
2 y 2 y 2 y 0.764 y 236.061 \ nonumber end { array}
Al analizar el movimiento con más detalle, podemos comenzar con algunas condiciones iniciales particulares. Un caso fácil es si (u_0 = v_0 = w_0 = 0 ), es decir, el electrón comienza en reposo. En ese caso no habrá fuerzas sobre él, y permanece en reposo todo el tiempo. Una condición inicial menos trivial es para (v_0 = 0 ), pero los otros componentes no son cero. En ese caso, la ecuación 8.5.7 muestra que ( phi ) es constante todo el tiempo. Lo que esto significa es que todo el movimiento tiene lugar en un plano ( phi = text {constant} ), y no hay movimiento “alrededor” del cable. Esto es de esperar, porque el componente ( rho ) de la velocidad da lugar a un componente (z ) de la fuerza de Lorenz, y el componente (z ) de la velocidad da lugar a una fuerza de Lorentz hacia el cable, y no hay ningún componente de fuerza “alrededor” (aumentando ( phi )) el cable. El electrón, entonces, se moverá en el plano ( phi = text {constant} ) a una velocidad constante (S = sS_C ), donde (s = sqrt {u_0 ^ 2 + w_0 ^ 2} ). (Recuerde que (u ) y (w ) son cantidades adimensionales, siendo los componentes de velocidad en unidades de la velocidad característica (S_C. )) Voy a acuñar las palabras perineme y aponeme para describir las distancias menor y mayor de los electrones del cable, es decir, los límites del movimiento. Estos límites se pueden encontrar estableciendo (u = 0 ) y (v_0 = 0 ) en la ecuación 8.5.10 (donde recordamos que (x = rho / rho_0 ), es decir, la relación del radial distancia del electrón en algún momento a su distancia radial inicial). Obtenemos
[ rho = rho_0e ^ {w_0 pm s} ]
para las distancias de aponeme (signo superior) y perineme (signo inferior). De la ecuación 8.5.8 podemos deducir que el electrón se mueve en ángulo recto con el cable (es decir, (w = 0 )) cuando está a una distancia
[ rho = rho_0e ^ { w_0}. ]
La forma de la trayectoria con v0 = 0 se encuentra integrando las ecuaciones 8.5.8 y 8.5.10. Es conveniente comenzar la integración en perineme para que u0 = 0 ys = w0, y el valor inicial de x (/) = ρ ρ0 sea 1. Para cualquier otra condición inicial, se pueden encontrar los valores de perineme de x y ρ de las ecuaciones 8.5.10 y 8.5.12 respectivamente. Las ecuaciones 8.5.10 y 8.5.8 pueden escribirse
[t = frac { rho_0} {S_C} int_1 ^ x frac {dx} {[2s ln x – ( ln x) ^ 2] ^ {1/2}} ]
y [z = St- rho_0 int_1 ^ x frac { ln x dx} {[2s ln x – ( ln x) ^ 2] ^ {1/2}}. ]
Hay singularidades en los integrandos en (x = 1 ) y ( ln x = 2s ), y, en Para sortear esta dificultad, es conveniente introducir una variable ( theta ) definida por
[ ln x = s (1- sin theta). ]
Las ecuaciones 8.5.14 y 15 se convierten en
[t = frac { rho_0e ^ s} {S_C} int _ { pi / 2} ^ 0 e ^ {- s sin theta} d theta ]
y [z = rho_0 se ^ s int _ { pi / 2} ^ 0 sin theta e ^ {- s sin theta} d theta. ]
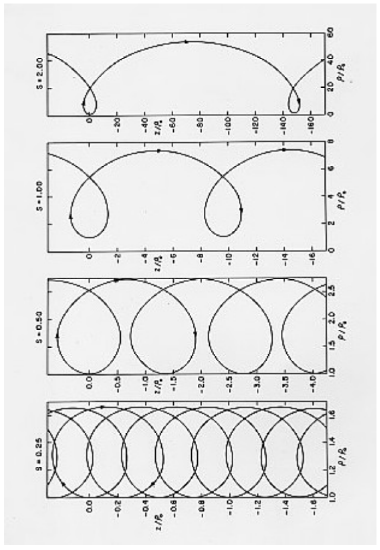
En la Figura ( text {VIII.4} ) se muestran ejemplos de estas trayectorias, aunque me temo que tendrá que girar el monitor hacia un lado para verlo correctamente. Se dibujan para (s = ) 0.25, 0.50, 1.00 y 2.00, donde (s ) es la relación entre la velocidad constante de los electrones y la velocidad característica (S_C ). Se supone que el cable está situado a lo largo del eje (z ) – ( ( rho = 0 )) con la corriente que fluye en la dirección positiva (z ). El electrón se desplaza en la dirección opuesta a la corriente. (Una partícula cargada positivamente se desplazaría en la misma dirección que la corriente). Las distancias en la Figura se expresan en términos de la distancia perinema ( rho_0 ). La forma de la ruta depende solo de (s ) (y no de ( rho )). Sin velocidad, el camino tiene una cúspide. El radio de curvatura (R ) en cualquier punto viene dado por (R = rho / s ).
Los mínimos de ( rho ) ocurren en ( rho_0 ) y ( theta = (4n + 1) pi / 2 ), donde (n ) es un número entero;
Los máximos de (z ) ocurren en ( rho = rho_0 e ^ s ) y ( theta = (4n + 2) pi / 2 );
Se producen máximos de ( rho ) en ( rho = rho_0e ^ {2s} ) y ( theta = (4n + 3) pi / 2 );
Mínimos de (z ) ocurren en ( rho = rho_0e ^ s ) y ( theta = (4n + 4) pi / 2 ).
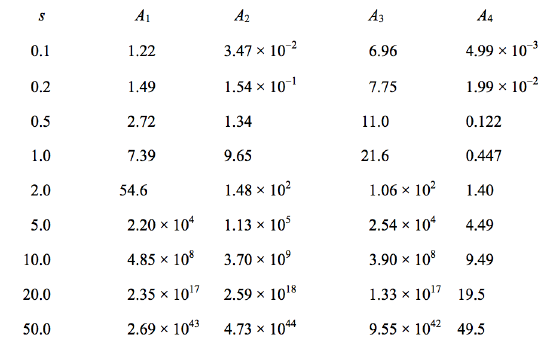
La distancia entre bucles sucesivos y el período de cada bucle varía rápidamente con la velocidad de los electrones, como se ilustra en la Tabla ( text {VIII.2} ). En esta tabla, (s ) es la velocidad de los electrones en unidades de la velocidad característica (S_C ), (A_1 ) es la relación de la distancia aponema a perinema, (A_2 ) es la relación de la distancia entre bucles a la distancia perineme, (A_3 ) es la relación del período por ciclo a ( rho_0 / S_C ), y (A_4 ) es la velocidad de deriva en unidades de la velocidad característica (S_C ).
( text {FIGURE VIII.4} )
Por ejemplo, para una corriente de 1 ( text {A} ), la característica la velocidad es (3.5176 veces 10 ^ 4 text {ms} ^ {- 1} ). Si un electrón se acelera a través de (8.7940 text {V} ), obtendrá una velocidad de (1.7588 text {m s} ^ {- 1} ), que es 50 veces la velocidad característica. Si el electrón comienza a esta velocidad moviéndose en la misma dirección que la corriente y (10 ^ {- 10} ) desde él, alcanzará una distancia máxima de (8.72 veces 10 ^ {10} ) megaparsecs (1 ( text {Mpc} = 3.09 times 10 ^ {22} text {m} )) de él, siempre que el Universo sea euclidiano. La distancia entre los bucles será (1.53 veces 10 ^ {12} text {Mpc} ), y el período será (8.60 veces 10 ^ {20} ) años, después de lo cual el electrón tendrá cubierto, a velocidad constante, una distancia total de (1.55 veces 10 ^ {12} text {Mpc} ). La velocidad de deriva será (1.741 veces 10 ^ 6 text {m s} ^ {- 1} ).
( text {TABLA VIII.2} )
Pasemos ahora a la consideración de casos donde (v_0 neq 0 ) para que El movimiento del electrón no está restringido a un plano. A primera vista, se podría pensar que dado que un componente de velocidad azimutal no genera fuerza de Lorenz adicional en el electrón, el movimiento difícilmente se verá afectado por un (v_0 ) distinto de cero, más que tal vez por una revolución alrededor del cable. En particular, para los componentes de velocidad inicial dados (u_0 ) y (w_0 ), las distancias perineme y aponeme (x_1 ) y (x_2 ) pueden parecer independientes de (v_0 ). Sin embargo, la referencia a la Tabla ( text {VIII.1} ) muestra que esto no es así en absoluto. La razón es que a medida que el electrón se acerca o se aleja del cable, los cambios en (v ) necesarios por la conservación del componente (z ) del momento angular se compensan con los cambios correspondientes en ( u ) y (w ) se hacen necesarios por la conservación de la energía cinética.
Dado que el movimiento está limitado arriba y abajo, siempre habrá algún tiempo cuando ( dot rho = 0 ). No hay pérdida de generalidad si cambiamos el origen del tiempo para elegir ( dot rho = 0 ) cuando (t = 0 ) y (x = 1 ). Desde este punto, por lo tanto, consideraremos solo aquellas trayectorias para las cuales (u_0 = 0 ). En otras palabras, seguiremos el movimiento desde un tiempo (t = 0 ) cuando el electrón está en una apis ( ( dot rho = 0 )). [El plural de apsis es apsides . La palabra ábside (plural ábside s) se usa a menudo en esta conexión, pero parece útil mantener una distinción entre el término arquitectónico ábside y el término matemático apsis .] Si esta apsis es perineme (para que ( dot rho = rho_1 ), (v_0 = v_1 ), (w_0 = w_1 )) o aponeme (para que ( dot rho = rho_2 ), (v_0 = v_2 ), (w_0 = w_2 )) depende del movimiento posterior.
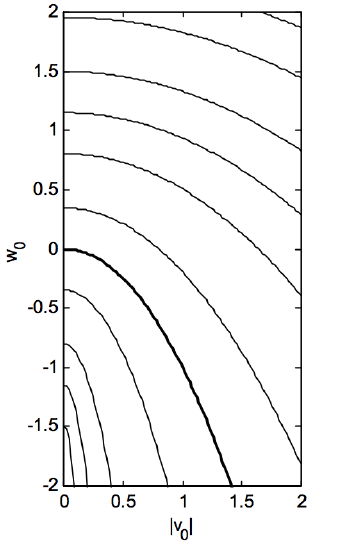
El electrón comienza, entonces, a una distancia del cable definido por (x = 1 ). Es interesante encontrar el valor de (x ) en la siguiente apis, en términos de los componentes de velocidad inicial (v_0 ) y (w_0 ). Esto se encuentra en la ecuación 8.5.10 con (u = 0 ) y (u_0 = 0 ). Los resultados se muestran en la Figura ( text {VIII.5} ). Esta Figura muestra loci de distancia de la siguiente apis constante, para valores de (x ) (que van desde la parte inferior izquierda a la parte superior derecha de la Figura) de 0.05, 0.10, 0.20, 0.50, 1, 2, 5, 10, 20, 50 , 100. La curva pesada es para (x = 1 ). Se verá de inmediato que, si (w_0> -v_0 ^ 2 ), (por encima de la curva pesada) el valor de (x ) en la segunda apsis es mayor que 1. (Recuerde que (v ) y (w ) son proporciones adimensionales, por lo que no hay ningún problema de desequilibrio dimensional en la desigualdad.) Por lo tanto, el electrón estaba inicialmente en el perineo y posteriormente se aleja del cable. Si, por otro lado, (w_0 <-v_0 ^ 2 ), (debajo de la curva pesada) el valor de (x ) en la segunda apsis es menor que 1. El electrón estaba inicialmente en aponema y luego se mueve más cerca del cable
( text {FIGURE VIII.5} )
El caso donde (w_0 = -v_0 ^ 2 ) es de especial interés para ellos las distancias perinema y aponema son iguales y, de hecho, el electrón se mantiene a una distancia constante del cable en todo momento. Se mueve en una trayectoria helicoidal a la deriva en la dirección opuesta a la dirección de la corriente convencional (I ). (Una partícula cargada positivamente se desplazaría en la misma dirección que (I ).) El ángulo de inclinación ( alpha ) de la hélice (es decir, el ángulo entre la velocidad instantánea y un plano normal al cable) viene dado por
[ tan alpha = -w / v, ]
donde (w ) y (v ) están restringidos por las ecuaciones
[w_0 = -v_0 ^ 2 ]
y [v ^ 2 + w ^ 2 = s ^ 2. ]
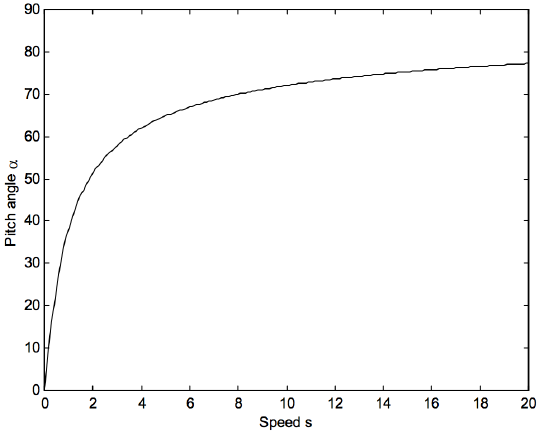
Esto implica que el ángulo de inclinación está determinado únicamente por ( s ), la relación de la velocidad (S ) del electrón a la velocidad característica (S_C ). En otras palabras, el ángulo de inclinación está determinado por la relación de la velocidad del electrón (S ) a la corriente (I ). La variación del ángulo de inclinación ( alpha ) con la velocidad (s ) se muestra en la Figura ( text {VIII.6} ). Esta relación es completamente independiente del radio de la hélice.
( text {FIGURA VIII.6} )
Si, (w_o neq -v_0 ^ 2 ) el electrón ya no se mueve en un hélice simple, y el movimiento debe calcularse numéricamente para cada caso. Es conveniente comenzar el cálculo en perineme con las condiciones iniciales (u_0 = 0 ), (w_0> -v_0 ^ 2 ), (x_0 = 1 ). Para otras condiciones iniciales, los valores perineme (y aponeme) de (u ), (v ), (w ) y ( rho ) se pueden encontrar fácilmente en las ecuaciones 8.5.10 (con ( u_0 = 0 )), 8.5.8 y 8.5.9. Comenzando, entonces, desde el perineo, las integraciones de estas ecuaciones toman las formas respectivas
[t = frac { rho_0} {S_C} int ^ x_1 [v_0 ^ 2 (1-1 / x ^ 2 ) + 2w_0 ln x – ( ln x) ^ 2] ^ {- 1/2} dx, ]
y [z = w_0S_Ct- rho_0 int ^ x_1v_0 ^ 2 (1- 1 / x ^ 2) + 2w_0 ln x – ( ln x) ^ 2] ^ {- 1/2} ln x dx ]
[ phi = v_0 int ^ x_1 [v_0 ^ 2 (1-1 / x ^ 2) + 2w_0 ln x – ( ln x) ^ 2] ^ {- 1/2} x ^ {- 2} dx. ]
[19459001 ] La integración de estas ecuaciones no es del todo trivial y se discute en el Apéndice (Sección 8A).
En general, el movimiento del electrón puede describirse cualitativamente de la siguiente manera. El movimiento está limitado entre dos cilindros de radios iguales a las distancias perinema y aponema, y la velocidad es constante. El electrón se mueve alrededor del cable en sentido horario o antihorario, pero, una vez iniciado, la sensación de este movimiento no cambia. La velocidad angular alrededor del cable es mayor en perineo y menor en aponema, siendo inversamente proporcional al cuadrado de la distancia desde el cable. Superpuesto al movimiento alrededor del cable hay una deriva general en la dirección opuesta a la de la corriente convencional. Sin embargo, por un breve momento cerca del perineo, el electrón se mueve temporalmente en la misma dirección que la corriente.
Se da un ejemplo del movimiento en las Figuras ( text {VIII.7} ) y 8 para los componentes de velocidad inicial (u_0 = 0 ), (v_0 = w_0 = 1 ). La distancia aponeme es 11.15 veces la distancia perineme. El intervalo de tiempo entre dos pasajes perinemes es 26.47 ( rho_0 / S_C ). El intervalo de tiempo para una revolución completa alrededor del cable ( ( phi = 360 ^ circ )) es 68.05 ( rho_0 / S_C ). En la Figura ( text {VIII.8} ), se supone que la corriente eléctrica convencional fluye hacia el plano del “papel” (pantalla de la computadora), lejos del lector. Las porciones de la trayectoria del electrón hacia donde se mueve el electrón desde el lector se dibujan como una línea continua, y las breves porciones cerca del perineo donde el electrón se aleja del lector se indican mediante una línea de puntos. Las marcas de tiempo en la Figura están a intervalos de (5 rho_0 / S_C ).
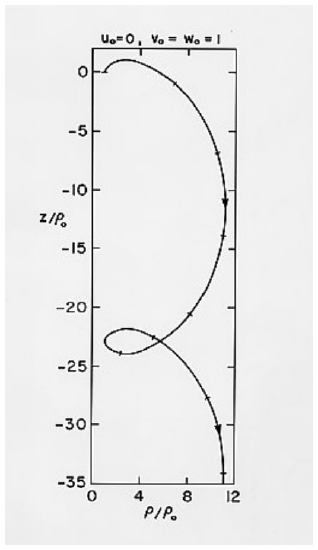
( text {FIGURE VIII.7} )
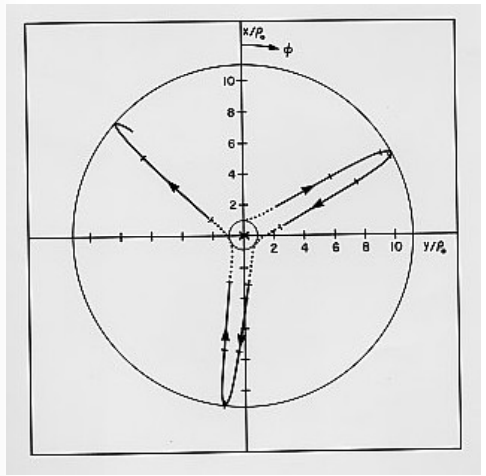
( text {FIGURE VIII.8} ) [19459002 ]