Un circuito en paralelo a menudo se llama un divisor de corriente por su capacidad de proporcionalizar o dividir la corriente total en partes fraccionarias.
Para entender lo que esto significa, analicemos primero un circuito paralelo , que determina las corrientes derivadas a través de resistencias individuales
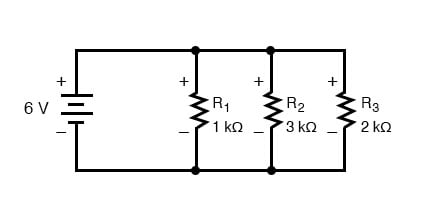
Sabiendo que los voltajes en todos los componentes en un circuito paralelo son los mismos, podemos completar nuestra tabla de voltaje / corriente / resistencia con 6 voltios en la fila superior:

Usando Ley de Ohm (I = E / R) podemos calcular la corriente de cada rama:

Sabiendo que las corrientes derivadas se suman en circuitos paralelos para igualar la corriente total, podemos llegar a la corriente total sumando 6 mA, 2 mA y 3 mA:

El paso final, por supuesto, es calcular la resistencia total. Esto se puede hacer con la Ley de Ohm (R = E / I) en la columna “total”, o con la fórmula de resistencia paralela de resistencias individuales. De cualquier manera, obtendremos la misma respuesta:

Una vez más, debería ser evidente que la corriente a través de cada resistencia está relacionada con su resistencia, dado que el voltaje en todas las resistencias es el mismo. En lugar de ser directamente proporcional, la relación aquí es de proporción inversa. Por ejemplo, la corriente a través de R 1 es el doble que la corriente a través de R 3 , que tiene el doble de resistencia que R 1 .
Si tuviéramos que cambiar el voltaje de suministro de este circuito, encontramos que (¡sorpresa!) Estas proporciones proporcionales no cambian:

Cálculo de relaciones actuales
La corriente a través de R 1 sigue siendo exactamente el doble que la de R 3 , a pesar de que la tensión de la fuente ha cambiado. La proporcionalidad entre las diferentes corrientes de ramificación es estrictamente una función de resistencia.
También recuerda a divisores de voltaje es el hecho de que las corrientes derivadas son proporciones fijas de la corriente total. A pesar del aumento cuádruple en el voltaje de suministro, la relación entre cualquier corriente derivada y la corriente total permanece sin cambios:

Ahora podemos ver por nosotros mismos el punto que señalamos al principio de esta página: Un circuito paralelo a menudo se llama un divisor de corriente por su capacidad de proporcionalizar o dividir la corriente total en partes fraccionarias .
La fórmula actual del divisor
Con un poco de álgebra, podemos derivar una fórmula para determinar la corriente de resistencia paralela dada nada más que la corriente total, la resistencia individual y la resistencia total:

La relación de resistencia total a resistencia individual es la misma relación que la corriente individual (ramificada) a la corriente total. Esto se conoce como la fórmula del divisor de corriente , y es un método abreviado para determinar las corrientes de derivación en un circuito paralelo cuando se conoce la corriente total.
Ejemplo de fórmula actual del divisor
Usando el circuito paralelo original como ejemplo, podemos volver a calcular las corrientes derivadas utilizando esta fórmula, si comenzamos conociendo la corriente total y la resistencia total:

Si se toma el tiempo de comparar las dos fórmulas de divisor, verá que son notablemente similares. Observe, sin embargo, que la relación en la fórmula del divisor de voltaje es R n (resistencia individual) dividida por R Total , y cómo la relación en la fórmula actual del divisor es R Total dividido por R n :

Fórmula actual del divisor vs. Fórmula del divisor de voltaje
Es bastante fácil confundir estas dos ecuaciones, haciendo retroceder las relaciones de resistencia. Una forma de ayudar a recordar la forma correcta es tener en cuenta que ambas relaciones en las ecuaciones del divisor de voltaje y corriente deben ser menores que una. ¡Después de todo, estas son ecuaciones divisor , no ecuaciones multiplicador ! Si la fracción está al revés, proporcionará una relación mayor que uno, lo cual es incorrecto.
Sabiendo que la resistencia total en un circuito en serie (divisor de voltaje) siempre es mayor que cualquiera de las resistencias individuales, sabemos que la fracción para esa fórmula debe ser R n sobre R Total [ 19459014]. Por el contrario, sabiendo que la resistencia total en un circuito paralelo (divisor de corriente) es siempre menor que cualquiera de las resistencias individuales, sabemos que la fracción para esa fórmula debe ser R Total sobre R n [19459014 ]
Ejemplo de aplicación del circuito divisor de corriente: circuito del medidor eléctrico
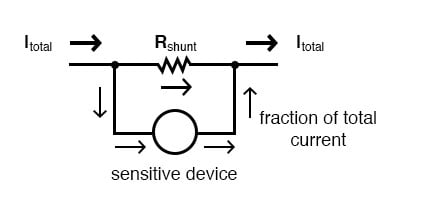
Los circuitos divisores de corriente también encuentran aplicación en los circuitos de medidores eléctricos, donde se desea que una fracción de la corriente medida se enrute a través de un dispositivo de detección sensible. Usando la fórmula del divisor actual, la resistencia de derivación adecuada puede dimensionarse para proporcionar la cantidad justa de corriente para el dispositivo en cualquier caso dado:
REVISIÓN:
- Proporción de circuitos paralelos, o “dividen”, la corriente total del circuito entre corrientes de derivación individuales, las proporciones dependen estrictamente de las resistencias: I n = I Total (R [19459013 ] Total / R n )
HOJAS DE TRABAJO RELACIONADAS: